Примеры расчета пластинок мкэ

Проведенное выше подробное изложение этапов и шагов численной реализации МКЭ дает возможность перехода непосредственно к примерам расчетов по МКЭ, иллюстрирующим возможности данного универсального метода расчета и скорость его сходимости. В табл. 1 приведены прогибы в центре (точка x=a/2, y=a/2) для квадратной а х а пластинки при двух условиях закрепления на контуре и двух вариантах загружения: равномерной нагрузкой q=const и сосредоточенной силой Р в центре. Используемые в табл.1 результаты взяты из [2]. Безразмерные параметры подсчитывались по формулам

. (30)

Таблица 1

NхN МКЭ	Шарнирный край		Жесткая заделка
	q=const	P в центре	q=const	P в центре
2х2	3.446	13.784	1.480	5.919
4х4	3.939	12.327	1.403	6.134
8х8	4.033	11.829	1.304	5.803
12х12	4.050	11.715	1.283	5.710
16х16	4.056	11.671	1.275	5.672
Решение [7] С.П.Тимошенко	4.062	11.60	1.26	5.60

В качестве конечных элементов для данной задачи в [2] использовались прямоугольные элементы с аппроксимацией перемещений неполным полиномом четвертой степени – по сравнению с аппроксимацией (14) добавлены слагаемые и . Такая аппроксимация соответствует изменению прогиба вдоль линий x=const и y=const по кубическому закону и повышает точность решения МКЭ при том же числе прямоугольных элементов.

Цифры NхN соответствуют сетке разбиения пластинки на конечные элементы. Анализ данных табл.1 показывает, что сходимость решения МКЭ при действии сосредоточенной силы несколько ухудшается по сравнению со случаем действия распределенной нагрузки. Тем на менее, уже результаты на сравнительно редкой сетке 8х8 дают по величине прогиба в центре погрешность лишь в 6,2% по сравнению с решением С. П. Тимошенко [7], высокая точность которого общеизвестна. Заметим также, что при использовании сетки 16х16 погрешность решения МКЭ по сравнению с [7] составляет уже лишь 0,15%, что соответствует отличной точности решения, тем более, что для современных ПЭВМ решение на числе узлов, равном 289, не представляет затруднений ( в каждом узле три неизвестных: прогиб и два угла поворота).

Проведем также сравнение результатов решения задачи МКЭ при использовании треугольных конечных элементов с результатами другого распространенного метода решения задач изгиба пластин – метода конечных разностей (МКР). В табл. 2 приведены безразмерные прогибы в центре , а также безразмерные величины изгибающих моментов в центре и в середине стороны контура жестко заделанной пластинки с размерами в плане (2a x 2a) при действии равномерно распределенной нагрузки, причем Решение МКР [8]

получено на сетке 64х 64, что дает весьма высокую точность решения задачи.

Таблица 2

NxN МКЭ	Жесткая заделка
4х4	2.2304	6.8873	-4.703
8х8	2.0854	8.5947	-11.149
16х16	2.0403	9.0205	-15.483
32х32	2.0285	9.1267	-17.940
64х64	2.0256	9.1532	-19.245
Решение МКР [8]	2.0288	9.1657	-20.507

Анализ результатов табл. 2 свидетельствует об устойчивой и достаточно быстрой сходимости МКЭ по всем рассматриваемым параметрам задачи, однако скорость сходимости по величине параметра является несколько меньшей. На рис. 10 приведены эпюры безразмерного параметра прогиба w и безразмерного изгибающего момента в сечении пластинки y=0.

Рис. 10

Характер изменения эпюр изгибающих , и крутящего моментов позволяет определить значения наибольших нормальных , и касательного напряжений. Наибольшие по толщине пластинки значения нормальных напряжений будут на нижней (знак «плюс» в формуле (31)) и верхней (знак «минус» в формуле (31)) поверхностях пластинки

. (31)

Отметим, что переход от безразмерных к размерным функциям осуществляется на основе формул

. (32)

При использовании энергетической теории прочности условие прочности упругих пластинок записывается в виде

, (33) где - расчетное сопротивление для материала пластинки.

Данные сопоставления решений МКЭ (треугольные конечные элементы) с решением МКР для шарнирно опертой пластинки с размерами в плане (2a x 2a) под действием равномерно распределенной нагрузки приведены в табл. 3 в виде параметров прогиба и изгибающего момента в центре пластинки. Цифры NхN соответствуют сетке разбиения пластинки на конечные элементы. Решение МКР [8] получено на сетке 64 х 64, что дает весьма высокую точность решения задачи.

Таблица 3

NxN МКЭ	Шарнирное опирание
4х4	6.9209	1.6734
8х8	6.6069	1.8548
16х16	6.5269	1.9003
32х32	6.5068	1.9117
64х64	6.5018	1.9145
Решение МКР [8]	6.4996	1.9151

Анализ результатов табл. 3 свидетельствует об устойчивой и быстрой сходимости МКЭ по рассматриваемым параметрам задачи. На рис. 11 приведены эпюры безразмерного параметра прогиба w и безразмерного изгибающего момента в сечении пластинки y=0.

Рис.11

Отметим, что на основе формул (31), (32), (33) можно проверить прочность пластинки при заданном уровне нагружения или установить из условия прочности материала пластинки (33) допускаемый уровень нагрузки.

Дополнительным свидетельством универсальности МКЭ является возможность расчета пластинки сложной формы, представленной на рис. 12. Габаритные размеры пластинки составляют а х а, действует равномерно распределенная нагрузка q=1. Отметим, что на сложном контуре пластинки условия опирания меняются вдоль одной из сторон контура. Подчеркнем, что наличие сложного контура пластинки исключает применение прямоугольных конечных элементов, поэтому расчет МКЭ проводится для треугольных конечных элементов.

Подчеркнем, что при заданных условиях закрепления применение вариационных методов расчета пластинок [9], а также и метода конечных разностей [8] сопряжено со значительными трудностями, но МКЭ достойно решает эту проблему.

Рис. 12

Для наглядной иллюстрации полученных результатов на рис. 13 приведены эпюры прогиба W и изгибающих моментов и .

Эпюра W Эпюра Эпюра

Рис. 13

Отметим, что осуществленное на рис. 13 представление информации о напряженно-деформированном состоянии пластинок является в настоящее время общепринятым в проектных организациях. Действительно, вывод информации в графическом виде позволяет выявить зоны с наибольшими изгибающими моментами и назначить армирование железобетонных пластинок.

В данных методических указаниях рассмотрены далеко не все возможные варианты применения МКЭ. Для более полного ознакомления с возможностями использования МКЭ в расчетах строительных конструкций авторы рекомендуют известную монографию О. С. Зенкевича [2].

В заключение раздела приводим порядок действий при расчете пластин МКЭ с составлением системы алгебраических уравнений, порядок которой совпадает с числом узлов сетки.

Напомним, что в упругой задаче теории упругости уравнение Р = К∙ представляет собой запись закона Гука в обобщенном виде, причем Р – вектор сил,  - вектор перемещений, К – матрица жесткости.

Порядок действий в алгоритме МКЭ:

1. Упругое плоское тело разбивается на элементы – на треугольники и прямоугольники.

2. Для каждого элемента составляется матрица жесткости К с использованием функции формы. Функция формы представляет собой способ аппроксимации неизвестной функции перемещений .

3. Матрицы жесткости элементов объединяются в единую матрицу жесткости для всего тела.

4. Решая систему уравнений Р = К∙, находят узловые перемещения .

5. С помощью уравнений теории упругости определяются деформации и напряжения в узловых точках тела.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Получить и при необходимости согласовать с преподавателем задание.

2. Изучить теоретический материал, пользуясь руководством и рекомендованной литературой (1час).

3. Записать бигармоническое уравнение и граничные условия задачи (0,25 часа).

4. Записать выражения для изгибающих момента и прогиба пластинки (0,25 часа).

5. Записать уравнение Софи Жермен и граничные условия с использованием конечно-элементных аналогов (0,5 часа).

6. Записать систему алгебраических уравнений МКЭ в матричном виде (0,25 часа).

7. Подготовить исходные данные для ПЭВМ по двум вариантам опирания и действии распределенной нагрузки (0,5 часа).

8. Выполнить расчеты пластинки на изгиб для двух вариантов опирания

по программе «Лира 9.0», описание которой приведено в приложении.

9. Построить в заданных сечениях пластины эпюры прогиба W и

изгибающих моментов для двух вариантов расчета (0,5 часа).

10. Провести расчет пластинки методом конечных разностей (0,5 часа).

11. Сопоставить решения МКЭ с данными расчетов МКР и сделать

соответствующие выводы (0,5 часа).

На выполнение расчетно-графической работы затрачивается примерно 5 часов из времени, отведенного на самостоятельную работу студента. Срок представления оформленной работы составляет три недели с момента выдачи задания.

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА О РАБОТЕ

Отчет о работе должен выполняться в соответствии с приведенными примерами расчета и содержать следующие разделы:

- вариант задания;

- постановка задачи;

- запись уравнения Софи Жермен и граничных условий;

- запись уравнения Софи Жермен и граничных условий с использованием конечно-элементных аналогов;

- запись системы линейных алгебраических уравнений МКЭ в табличной форме;

- результаты расчетов на ПЭВМ МКЭ в виде эпюр прогиба W и изгибающих моментов для двух вариантов опирания пластинок;

- результаты расчета пластинки методом конечных разностей (МКР);

- сопоставление решения МКЭ и решения МКР.

При оформлении работы численные результаты необходимо иллюстрировать чертежами, выполненными в масштабе с использованием чертежных принадлежностей или компьютерной графики.

Работа оформляется на одной стороне листов формата А 4.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие допущения принимаются в теории тонких пластинок?

2. Как выражаются деформации пластинки через ее прогиб?

3. Как записывается дифференциальное уравнение Софи Жермен изгиба элемента пластинки?

4. Как записываются граничные условия для свободной от закреплений стороны контура пластинки?

5. Как формулируются граничные условия на защемленных сторонах контура пластинки?

6. Каковы граничные условия на шарнирно опертых сторонах контура пластинки?

7. В чем особенности применения МКЭ к расчету пластинок?

8. Каковы преимущества использования МКЭ по сравнению с другими методами расчета пластинок?

9. На какие конечные элементы можно разбить прямоугольную пластинку?

10. Какие конечные элементы необходимо использовать для пластинок со сложным контуром?

11. Как записывается система линейных алгебраических уравнений (СЛАУ) зависимости смещений узлов КЭ от узловых сил?

12. Какой вид имеет СЛАУ связи смещений узлов от узловых сил для всей пластинки?

13. Какие требования предъявляются к аппроксимирующим функциям в МКЭ по методу перемещений?

14. Чему равны значения функций формы для различных узлов КЭ?

15. Какова физическая сущность определения вектора узловых перемещений при расчете пластинок МКЭ?

16. Какова последовательность решения задачи изгиба пластинки методом конечных элементов (МКЭ)?

17. Какое количество степеней свободы имеет прямоугольный конечный элемент?

18. Какое количество степеней свободы соответствует треугольному конечному элементу?

19. По каким формулам вычисляются изгибающие и крутящий моменты в пластинке?

20. По каким формулам вычисляются напряжения , и 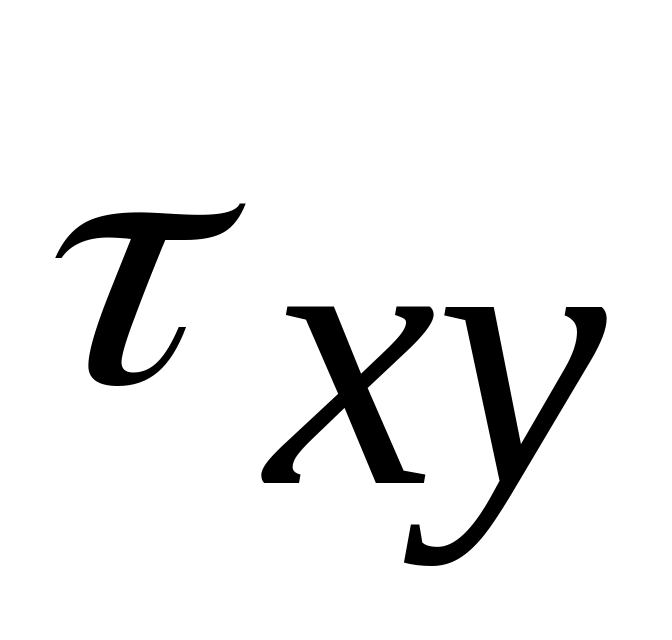в пластинке?

21. Элементами каких инженерных сооружений являются пластинки?

ВАРИАНТЫ ЗАДАНИЙ

Схема закрепления пластинок на контуре – цифра 1

«0» - свободный край пластинки,

«1» - шарнирное опирание края пластинки,

«2» - жесткая заделка края пластинки.

№	x=0	x=a	y=0	y=b	№	x=0	x=a	y=0	y=b
1	2	1	2	0	12	1	0	2	2
2	1	2	0	0	13	2	0	0	1
3	0	0	2	1	14	0	2	1	1
4	2	0	1	2	15	1	1	2	0
5	2	0	1	1	16	0	1	1	2
6	0	2	0	1	17	2	1	1	0
7	0	1	2	0	18	1	2	1	0
8	0	2	1	2	19	0	1	2	1
9	2	2	0	1	20	1	1	0	2
10	2	2	0	0	21	2	2	1	0
11	1	0	2	2	22	2	2	0	1

Схема нагружения пластинок – цифра 2

1 - равномерная нагрузка q=const по всей поверхности,

2 - нагрузка q=const при 0<x<a/2,

3 - нагрузка q=const при a/2<x<a,

4 - нагрузка q=const при 0<y<b/2,

5 - нагрузка q=const при b/2<y<b,

6 - нагрузка q=const при 0<x<a/2, 0<y<b/2,

7 - нагрузка q=const при 0<x<a/2, b/2<y<b,

8 - нагрузка q=const при a/2<x<a, 0<y<b/2,

9 - нагрузка q=const при a/2<x<a, b/2<y<b.