Тема 6: модель повторных независимых испытаний: формула бернулли и ее асимптотические приближения
Если вероятность наступления события A в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события A. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события A в каждом испытании одна и та же. Описанная последовательность независимых испытаний называется схемой Бернулли.
Пусть производится n независимых опытов, в каждом из которых с одной и той же вероятностью p может наступить некоторое событие A. Требуется для заданного числа k найти вероятность следующего события: в n опытах событие A наступит ровно k раз.
Чтобы
подчеркнуть зависимость полученного
выражения от n
и k, обозначим
его через
.
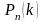Вероятность появления события A
в n
независимых испытаниях ровно k
раз равна:
.
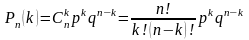Полученная формула называется формулой Бернулли.
В ряде случаев требуется определить вероятности появления события А менее k раз (X<k), более k раз (X>k), не менее k раз (X≥k), не более k раз (X≤k). В этих случаях могут быть использованы формулы:
,
,
,
.
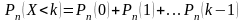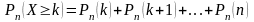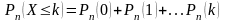Наивероятнейшее число появлений события в n независимых испытаниях определяют по формуле:
.
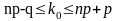Количество n опытов, которые нужно произвести для того, чтобы с вероятностью не меньше P можно было утверждать, что данное событие произойдёт по крайней мере один раз, находится по формуле:
,
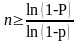где p – вероятность появления этого события в каждом опыте.
Теорема.
Если вероятность события p
наступления события А в
каждом испытании очень мала:
при неограниченном увеличении числа
испытаний (такие события называются
редкими), причем произведение
np стремится
к постоянному числу λ, то
вероятность
того, что событие А появится k
раз в n независимых
испытаниях, удовлетворяет предельному
равенству:
.
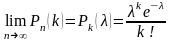Эта
формула называется формулой Пуассона
(должны выполняться следующие условия:
;
;
).
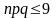начения
функции Пуассона
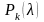приведены в Приложении №3. Приведём
значения функции Пуассона для небольших
значений λ:
λ k |
0,1 |
0,2 |
0,3 |
0,4 |
0,6 |
0,7 |
0,8 |
0,9 |
0 |
0,904 |
0,818 |
0,740 |
0,670 |
0,548 |
0,496 |
0,449 |
0,406 |
1 |
0,090 |
0,163 |
0,222 |
0,268 |
0,329 |
0,347 |
0,359 |
0,365 |
2 |
0,004 |
0,016 |
0,033 |
0,053 |
0,098 |
0,121 |
0,143 |
0,164 |
3 |
0,0002 |
0,0011 |
0,0033 |
0,0072 |
0,0198 |
0,0284 |
0,0383 |
0,0494 |
4 |
|
0,0001 |
0,0003 |
0,0007 |
0,0030 |
0,0050 |
0,0077 |
0,0111 |
5 |
|
|
|
0,0001 |
0,0004 |
0,0007 |
0,0012 |
0,0020 |
6 |
|
|
|
|
|
0,0001 |
0,0002 |
0,0003 |
Локальная теорема Муавра-Лапласа. Если вероятность p наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А произойдет k раз в n независимых испытаниях при достаточно большом числе n, приближенно равна:
φ(x),
где φ
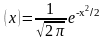и
.
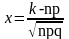Чем больше n, тем точнее указанная приближенная формула, называемая локальной формулой Муавра-Лапласа.
Обычно
этой формулой пользуются тогда, когда
.
Значения функции φ(x)
приведены в Приложении №1. Отметим