Тема 4: условная вероятность, зависимость и независимость событий. Формула байеса

При совместном рассмотрении двух случайных событий A и B часто возникает вопрос: насколько связаны эти события друг с другом, в какой мере наступление одного из них влияет на возможность наступления другого?

Для характеристики зависимости одних событий от других вводится понятие условной вероятности. Пусть ≠0, тогда отношение 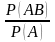называется условной вероятностью события В при условии наступления события А. Такая вероятность обозначается P(B/A). По определению имеем следующее равенство:

P (B/A) = .

Теорема 1 (умножения вероятностей). Вероятность совместного наступления двух событий равна вероятности одного из этих событий при условии другого, умноженной на вероятность самого условия:

.

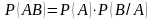Утверждение теоремы непосредственно следует из определения условной вероятности и допускает распространение на случай большего числа сомножителей:

P( )= .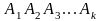

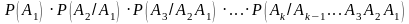Если появление события А не зависит от того, произошло или нет событие В, то условная вероятность А в предположении, что событие В наступило, будет равна вероятности А, т.е. P(A/B)=P(A). Подставляя в формулу умножения вероятностей вместо P(A/B) вероятность P(A), получим: P(AB)=P(A)·P(B).

Если это соотношение выполняется, то события А и В называются независимыми.

Утверждение 1. Пусть события А и В – независимы. Тогда независимы также события 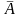и В, А 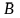и , и .

Несколько событий называют попарно независимыми, если каждые два из них независимы.

Несколько событий называют независимыми в совокупности, если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Отметим, что требование независимости событий в совокупности сильнее требования их попарной независимости.

Утверждение 2. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

.

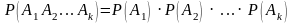Если события , ,…, - независимы в совокупности, то и противоположные им события 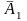, ,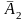…, 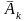также независимы в совокупности.

Теорема 2. Вероятность появления хотя бы одного из событий , ,…, , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:

.

Следствие. Если события , ,…, имеют одинаковую вероятность, равную p, то вероятность появления хотя бы одного из этих событий =1-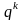 , где q=1-p.

Теорема 3. Если событие A может произойти только при условии появления одного из событий (гипотез) , , …,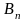 , образующих полную группу, то вероятность события A равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события A:

.

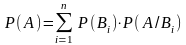Указанная формула называется формулой полной вероятности.

В тесной связи с формулой полной вероятности находится так называемая формула Байеса. Она относится к той же ситуации, что и формула полной вероятности (событие A может наступить только вместе с одним из n попарно несовместных событий , , …, ). Допустим, что опыт уже произведен, и нам известно, что событие A наступило. Сам по себе этот факт еще не позволяет сказать, какое из событий , , …, имело место в проделанном опыте. Можно, однако, поставить такую задачу: найти вероятности 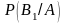, …, каждой из гипотез в предположении, что наступило событие A (такие вероятности называются апостериорными в отличие от вероятностей , …, , 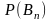вычисляемых до опыта и называемых априорными).

С одной стороны, вероятность совмещения двух зависимых событий определяется по формуле: ,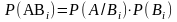

а с другой стороны, имеем: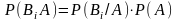 . Приравнивая правые части, получим: 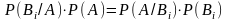, откуда следует: , где знаменатель рассчитывается по формуле полной вероятности. Таким образом, апостериорная вероятность определяется по формуле:

,

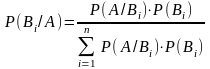которая называется формулой Байеса. Запомнить ее нетрудно: в знаменателе стоит выражение для полной вероятности события A, а в числителе – одно из слагаемых этого выражения. Формула Байеса дает возможность «пересмотреть» вероятности гипотез с учетом наблюдавшегося результата опыта.