Тема 3: вероятностные модели

Теория вероятностей изучает математические модели случайных явлений, но не всех, а только таких, которые обладают свойством статистической устойчивости относительных частот. В любой вероятностной модели считаются известными все возможные неразложимые исходы эксперимента. Однако множество таких исходов может быть конечным или бесконечным. В зависимости от этого строят различные вероятностные модели.

Аксиомы, задающие само понятие вероятности:

А.1 Каждому событию А поставлено в соответствие неотрицательное число P(А), называемое вероятностью события А: ≥0.

Так как любое событие есть множество, то вероятность события есть функция, заданная на множестве.

А.2 Вероятность достоверного события равна 1: .

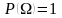А.3 Вероятность суммы несовместных событий равна сумме вероятностей этих событий, т.е. если 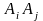=Ø ( I ≠ j ), то

= .

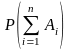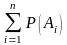Из аксиом А.1–А.3 следуют основные свойства вероятности:

1) Если Ø – невозможное событие, то (Ø)=0.

2) .

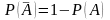3) При 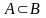справедливо неравенство: ≤

4) Для любых двух событий А и В: .

(это свойство называется расширенной формулой сложения).

5) Для любых событий , ,…, : .

Теорема. Сумма вероятностей событий , ,…, , образующих полную группу, равна единице: .

Модель Лапласа (классическая модель): число равновозможных результатов – конечно.

.

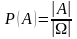Эта формула дает классическое определение вероятности: вероятность случайного события А вычисляется как отношение числа элементарных исходов, благоприятствующих появлению А, к общему числу возможных элементарных исходов.

Обычная схема подсчета вероятности случайного события А для описанной выше модели выглядит так:

1. выбирается (с обоснованием равновозможности элементарных исходов);

2. подсчитывается количество элементов в ;

3. подсчитывается количество элементов в А;

4. вычисляется вероятность .

Для испытаний, число равновозможных исходов в которых – бесконечно строится геометрическая модель: элементарные исходы интерпретируются как выбор наудачу точки из некоторого множества в . Предполагается, что множество имеет некоторую геометрическую форму, которую можно каким-либо образом измерить (определить длину – в 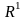, либо вычислить площадь – в , объем – в и т.п.). Событием называется следующее: выбранная точка принадлежит заданной части фигуры. Вероятность такого события определяется как отношение меры (обозначение mes) части фигуры А к мере всей фигуры Ω: . В описанной геометрической модели остаются в силе все аксиомы А.1 – А.3, соответственно выполняются все свойства 1 – 5.

Принцип практической уверенности:

В статистике все события подразделяют на «маловероятные», «высоковероятные» и «типичные». Интуитивно понятно: если известно, что данное событие имеет вероятность, близкую к нулю, то, скорее всего, в единичном испытании оно не произойдет. Если же вероятность события близка к единице, то практически можно считать, что в единичном испытании это событие наступит.

Естественно возникает вопрос о значении порогового уровня для слишком малой и слишком большой вероятности. Экономисты традиционно в качестве порогового значения, отделяющего «малые» вероятности используют (пятипроцентный уровень значимости). Для «больших» вероятностей такое значение равно

1-α=0,95. Соответственно, если вероятность случайного события А удовлетворяет условию: 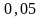≤ ≤ 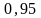, то такое событие считается «типичным», следовательно, его наступление в эксперименте можно объяснить случайностью. Если вероятность случайного события А меньше 0,05, но, тем не менее, событие произошло, то это можно считать подозрительным фактом; аналогично подозрительным будет и ненаступление «высоковероятного» события.