- •Часть 1. Теория вероятностей
- •Тема 1: элементы теории множеств и комбинаторики
- •Задачи для самостоятельного решения:
- •Тема 2: действия над событиями
- •Задачи для самостоятельного решения:
- •Тема 3: вероятностные модели
- •Задачи для самостоятельного решения:
- •Тема 4: условная вероятность, зависимость и независимость событий. Формула байеса
- •Задачи для самостоятельного решения:
- •Тема 6: модель повторных независимых испытаний: формула бернулли и ее асимптотические приближения
- •Свойства функции φ(X):
- •Задачи для самостоятельного решения:
- •Тема 7: производящая функция
- •Задачи для самостоятельного решения:
- •Подготовка и проведение контрольной работы по теме «случайные события»
- •Приложение №2
Часть 1. Теория вероятностей
Тема 1: элементы теории множеств и комбинаторики
Обозначим |A| - количество элементов множества А. Число элементов пустого множества равно нулю: |Ø|=0. Число элементов множества, образованного единственным элементом, равно единице: |A|=1. Важную роль в комбинаторике играют следующие правила:
Правило
сложения: для любых множеств
 и В таких, что
и В таких, что
 Ø
верно: |A+B|=|A|+|B|.
Ø
верно: |A+B|=|A|+|B|.
Правило
умножения: Для любых конечных
множеств А и В :
|A B|=|A|·|B|.
B|=|A|·|B|.
На практике это означает, что если первый элемент а выбирается из n возможных, а второй элемент b - из k возможных, то число упорядоченных пар вида (a,b) равно произведению n·k.
Правило вычитания: Для каждой части А конечного множества В верно: |A-B|=|A|-|B|.
Правило объединения: Для любых конечных множеств А и В верно:
|A B|=|A|+|B|-|A B|.
Правило объединения для трех множеств:
|A B C|=|A|+|B|+|C|-|A B|-|B C|-|A C|+|A B C|.
Перестановками из n элементов называют всевозможные n –расстановки, каждая из которых содержит все эти элементы по одному разу и которые отличаются друг от друга лишь порядком элементов.
Число
n –
перестановок обозначают через
 .
Чтобы узнать, сколько перестановок
можно составить из n
элементов, надо перемножить все
натуральные числа от 1 до n.
Это произведение обозначают n!
(читается n-факториал):
.
Чтобы узнать, сколько перестановок
можно составить из n
элементов, надо перемножить все
натуральные числа от 1 до n.
Это произведение обозначают n!
(читается n-факториал):
 =
1·2·3·
=
1·2·3·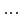 ·
·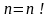
В частности, если n=0, то полагают 0!=1.
Пусть
конечное множество А содержит
n элементов. Часть
В множества А,
составленную из m
элементов, будем называть выборкой
(без возвращения) m
из n
элементов множества А.
Число всех таких выборок определяется
числами m, n
и обозначается символом
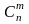 .
Вместо слова выборка говорят также
сочетание: m-сочетаниями
из n
элементов называют всевозможные
m-расстановки,
составленные из этих элементов и
отличающиеся друг от друга составом,
но не порядком элементов. Число таких
сочетаний вычисляется по формуле:
.
Вместо слова выборка говорят также
сочетание: m-сочетаниями
из n
элементов называют всевозможные
m-расстановки,
составленные из этих элементов и
отличающиеся друг от друга составом,
но не порядком элементов. Число таких
сочетаний вычисляется по формуле:
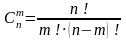 .
.
Числа обладают следующими свойствами:
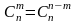 ;
; ;
;для любого m, удовлетворяющего условию 1≤m≤n, справедливо равенство:
 .
. .
.
Классической
задачей комбинаторики является также
задача о числе размещений:
сколько существует способов, чтобы
выбрать m из n
различных элементов и разместить их по
m различным местам?
Число размещений m
элементов из n
обозначается
 .
Так как сначала мы выбираем m
из n элементов, а
затем упорядочиваем их, то для определения
числа размещений надо перемножить число
сочетаний
на число перестановок
.
Так как сначала мы выбираем m
из n элементов, а
затем упорядочиваем их, то для определения
числа размещений надо перемножить число
сочетаний
на число перестановок
 :
:
 .
.
Если из конечного множества A, содержащего n элементов, m раз выбирать по одному элементу, каждый раз возвращая его обратно, то получим множество из m элементов, которое называют выборкой с повторениями или размещением с повторениями.
Число
всех размещений с повторениями из n
элементов по m
зависит, очевидно, только от n
и m
(а не от природы множества A).
Обозначим это число
 .
Из правила произведения следует, что
это число равно:
.
Из правила произведения следует, что
это число равно:
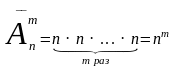 .
.
Если
в перестановках из общего числа n
элементов есть k
различных элементов, при этом 1-й
элемент повторяется
 раз, 2-й
элемент -
раз, 2-й
элемент -
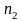 раз, k-й
элемент -
раз, k-й
элемент -
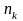 раз, причем
раз, причем
 ,
то такие перестановки называют
перестановками
с повторениями из
n
элементов.
Число перестановок с повторениями из
n
элементов равно:
,
то такие перестановки называют
перестановками
с повторениями из
n
элементов.
Число перестановок с повторениями из
n
элементов равно:
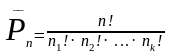 .
.
Пусть
множество A содержит n•m элементов, среди
которых по m одинаковых элементов каждого
из n различных типов. Число способов
выбрать m элементов из множества A
называется выборкой с повторениями
(или сочетаниями с повторениями) и
вычисляется по формуле: