2. Метод серединных квадратов.

Одной из исторически первых процедур получения псевдослучайных чисел была процедура, получившая название метода серединных квадратов. Пусть имеется 2n-разрядное число, меньшее 1: . Возведем его в квадрат: , а затем отберем средние 2n разрядов , которые и будут являться очередным числом псевдослучайной последовательности. Например, если начальное число , , т. е. , затем , т.е. , и т. д.

Недостаток этого метода — наличие корреляции между числами последовательности, а в ряде случаев случайность вообще может отсутствовать. Например, если х₀=0,4500, то , , , , , и т. д. Кроме того, при некоторых i* вообще может наблюдаться вырождение последовательности, т. е. , при i>i*. Это существенно ограничивает возможности использования метода серединных квадратов.

3. Конгруэнтные процедуры генерации. Широкое применение при моделировании систем на ЭВМ получили конгруэнтные процедуры генерации псевдослучайных последовательностей, представляющие собой арифметические операции, в основе которых лежит фундаментальное понятие конгруэнтности. Два целых числа и конгруэнтны (сравнимы) по модулю m, где m — целое число, тогда и только тогда, когда существует такое целое число k, что , т. е. если разность делится на m и если числа и дают одинаковые остатки от деления на абсолютную величину числа m. Например, 1984=4 (mod 10), 5008 = 8 (mod 103) и т. д.

Конгруэнтные процедуры являются чисто детерминированными, так как описываются в виде рекуррентного соотношения, когда функция Ф имеет вид

, (**)

где , , , – — неотрицательные целые числа.

Раскроем данное рекуррентное соотношение:

,

,

,

…,

.

Если заданы начальное значение Х₀, множитель и аддитивная константа , то это соотношение однозначно определяет последовательность целых чисел {X_i}, составленную из остатков от деления на М членов последовательности . Таким образом, для любого i>=1 справедливо неравенство X_i<M. По целым числам последовательности {X_i} можно построить последовательность рациональных чисел из единичного интервала (0, 1). Конгруэнтная процедура получения последовательностей псевдослучайных квазиравномерно распределенных чисел может быть реализована мультипликативным либо смешанным методом.

Мультипликативный метод. Задает последовательность неотрицательных целых чисел {X_i}, не превосходящих М, по формуле

т. е. это частный случай соотношения (**) при .

В силу детерминированности метода получаются воспроизводимые последовательности. Требуемый объем машинной памяти при этом минимален, а с вычислительной точки зрения необходим последовательный подсчет произведения двух целых чисел, т. е. выполнение операции, которая быстро реализуется современными ЭВМ.

Для машинной реализации наиболее удобна версия , где р — число цифр в системе счисления, принятой в ЭВМ (р=2 для двоичной и р= 10 для десятичной машины); g — число битов в машинном слове. Тогда вычисление остатка от деления на М сводится к выделению g младших разрядов делимого, а преобразование целого числа Х( в рациональную дробь из интервала осуществляется подстановкой слева от X, двоичной или десятичной

запятой.

Алгоритм построения последовательности для двоичной машины в сводится к выполнению таких операций:

1. Выбрать в качестве Х₀ произвольное нечетное число.

2. Вычислить коэффициент , где t — любое целое положительное число.

3. Найти произведение , содержащее не более 2g значащих разрядов.

4. Взять g младших разрядов в качестве первого члена последовательности Х₁ а остальные отбросить.

5. Определить дробь из интервала (0, 1).

6. Присвоить X₀=X₁.

7. Вернуться к п. 3.

Пример. Необходимо получить числа последовательности для случая g=4, используя приведенный алгоритм мультипликативного метода. Для этого выполняем следующие действия:

1. Выбираем X₀₁₀=7 (в десятичной системе счисления) или X₀=0111 (в двоичной системе счисления).

2. Найдем t=1, тогда или 5; пусть , .

3. Рассчитываем произведение , берем g младших разрядов, вычисляем X₁ и присваиваем X₀=X₁, т. е. выполняем п. 3 — 7 алгоритма:

а) ; X₁=0011, ;

б) ; X₂=1111,

в) ; X₃=1011, ;

г) ; X₄=0111, ;

Смешанный метод. Позволяет вычислить последовательность неотрицательных целых чисел {X_i}, не превосходящих М, по формуле

т. е. в отличие от мультипликативного метода .С вычислительной точки зрения смешанный метод генерации сложнее мультипликативного на одну операцию сложения, но при этом возможность выбора дополнительного параметра позволяет уменьшить возможную корреляцию получаемых чисел. Качество конкретной версии такого генератора можно оценить только с помощью соответствующего машинного эксперимента.

В настоящее время почти все пакеты прикладных программ универсальных ЭВМ для вычисления последовательностей равномерно распределенных случайных чисел основаны на конгруэнтной процедуре.

Преобразование квазиравномерной последовательности в числа с другим законом распределения.

Рассмотрим функцию распределения

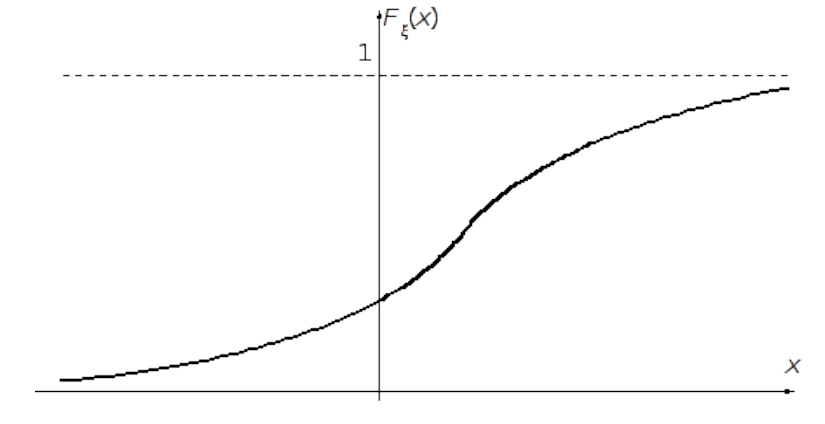
Преобразование чисел в нормально распределенную последовательность осуществляется с помощью функции, обратной функции : .

Для неравномерного распределения преобразование соответствует .

Плотность экспоненциального распределения , , – величина, обратная математическому ожиданию x, то есть .

.

.

Преобразование равномерных чисел в числа с экспоненциальным законом распределения, таким образом, имеет вид:

, где - равномерные случайные величины, -экспоненциальные случайные величины.

,

,

.

Для нормального распределения аналитический вид вычислить не удается, поэтому в качестве используют сумму достаточно большого числа равномерно распределенных чисел.