Лабораторна робота №3

Тема: аналіз САУ електроприводом постійного струму з незалежним збудженням.

Мета: отримати навички в математичному описі двигуна постійного струму з незалежним збудженням, а також моделювання динаміки САУ за допомогою Matlab.

Теоретичні відомості. Оскільки двигун постійного струму є виконавчим механізмом багатьох систем керування, має сенс досконально розглянути його математичний опис. При аналізі роботи електроприводу всі параметри елементів його механічної частини (вал двигуна, трансмісія, деформуючий інструмент, робоче тіло, над яким виробляють технологічну операцію), приводять до одного елементу - валу двигуна.

Математична модель електроприводу у вигляді системи диференціальних рівнянь:

(3.1)

Тут відомими функціями часу є:

- керуючий вплив (ЕРС джерела живлення електродвигуна-теля) ();

- обурючий вплив (момент власної навантаження електроприводу) ( ).

Відомими також є параметри системи:

- постійна машини; - (двигун з постійним магнітним потоком і компенсацією магнітного потоку якоря);

- активний опір силових ланцюгів ТП-Д;

- індуктивність силових ланцюгів ТП-Д;

- момент інерції, приведений до ротору електродвигуна.

Невідомими в цій системі є:

- швидкість обертання двигуна;

- струм якоря , відповідний електромагнітного моменту , .

Лінійна диференціальна система рівнянь (3.1) перетворюється в алгебраїчну лінійну систему рівнянь в образі Лапласа:

(3.2)

Рішення розімкнутої системи (1.2) відносно и , має вигляд:

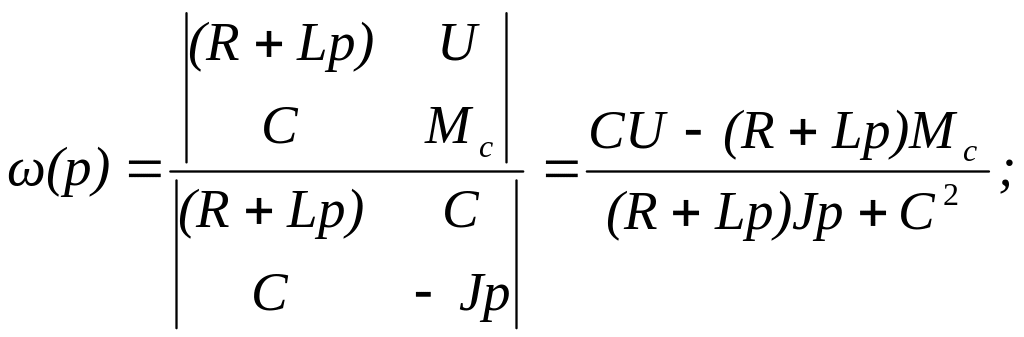
Після нескладних перетворень отримаємо рішення і розімкнутої системи у вигляді передавальних функцій по каналам управління і обурення:

(3.3)

(3.4)

де

Використовуючи вирази (3.2), (3.3), (3.4) і не торкаючись специфічних питань, пов'язаних з: джерелами живлення (тиристорні перетворювачі); підлеглим регулюванням; локальними зворотними зв'язками і т.д., легко отримати структурні схеми замкнутих електромеханічних систем , керованих по швидкості і моменту з перехресними і не перехресними зв'язками (див. рис.3.1 - 3.4).

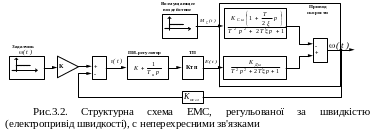
Крім цих структурних схем отримаємо відповідне аналітичне рішення замкнутої системи електропривода по швидкості . Для цього незалежну змінну - напруга висловимо через задаючий вплив, регульовану координату - швидкість і негативний зворотний зв'язок з коефіцієнтом . Тобто:

(3.5)

де - твір передавальних функцій регулятора і тиристорного перетворювача.

Підставивши в систему (3.2) вираз (3.5) для , отримаємо систему рівнянь (3.6) для замкнутої системи управління за швидкостю:

(3.6)

Рішення системи (1.6) для , , має вигляд:

Після перетворень отримаємо передавальні функції швидкості і електромагнітного моменту для замкнутої системи за швидкістю:

(3.7)

(3.8)

Можна вибрати , що відповідає ПІ-регулятору і лінійному коефіцієнту посилення тиристорного перетворювача.

Аналогічним чином отримаємо аналітичне рішення по моменту , використовуючи негативний зворотний зв'язок з коефіцієнтом . Висловимо незалежну змінну через задаючий вплив і регульовану координату , відповідну моменту:

(3.9)

Підставивши в систему (3.2) вираз (3.9) для , отримаємо систему рівнянь (1.10) для замкнутої системи управління з моменту :

(3.10)

Знайдемо рішення системи (3.10) для , :

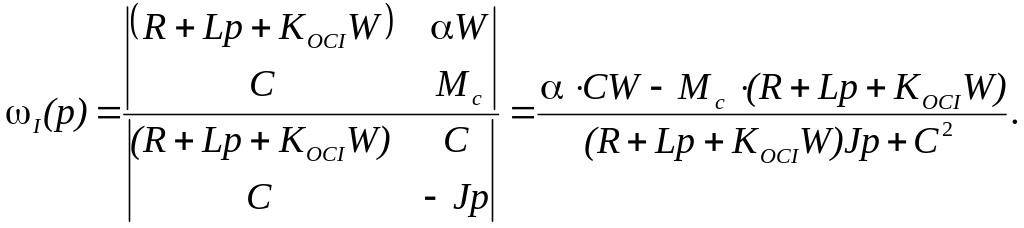
Після перетворень отримаємо передавальні функції швидкості і електромагнітного моменту для замкнутої системи за моментом:

(3.11)

(3.12)

де - можливий варіант.

Аналіз електроприводу, регульованого по потужності, виходить за межі лінійної постановки даного завдання. Вихідна система рівнянь (3.1) трансформується в систему рівнянь (3.13), елементами якої є тільки характеристики потужностей, а саме:

(3.13)

Тут:

- електрична потужність, що подається в якір електродвигуна;

- теплова потужність, що розсіюється в якорі двигуна;

- потужність, що запасається (віддається) індуктивністю якоря двигуна;

- електромеханічна потужність двигуна (корисна потужність);

- потужність, пов'язана з кінетичною енергією ЕМС;

- механічна потужність сил опору, що перешкоджають руху системи.

Напруга джерела живлення є єдиним керуючим впливом, регулюючи яким в замкнутих системах управління, підтримують на заданому рівні струм якоря, швидкість обертання двигуна, а також електромеханічну потужність. Тому, ця напруга є незалежною функцією часу не тільки в (3.1), а й у системі (3.13). Незалежною функцією також є збурючий момент навантаження , що залежить від технологічних параметрів. У зв'язку з тим, що перераховані елементи в системі рівнянь (1.13), названі незалежні функції входять як співмножники, в цій системі виходить шість невідомих різних типів потужностей. Тому, система (3.13) - незамкнута з точки зору її рішення щодо потужностей. Якщо завдання вирішувати щодо і , то система (3.13) стає нелінійною і до неї неможливо застосувати перетворення Лапласа.

Наступний важливе питання. Який з перерахованих типів потужностей, необхідно підтримувати в заданому режимі в ЕМС? Це може бути або корисна електрична потужність ( ), виходячи з системи (3.13), остання має вигляд:

(3.14)

(3.15)

або корисна електромеханічна потужність (та ж система (3.13) з лівою частиною рівнянь, яка цікавить нас):

(3.16)

(3.17)

Краще використовувати електромеханічну потужність , так як вона явно характеризує механічний об'єкт (права частина виразу (3.16) не містить електричних величин), а права частина виразу (3.17) не містить механічних характеристик. Подібною якістю не відрізняється корисна електрична потужність, що видно з виразів (3.14) і (3.15). Отже, електромеханічна потужність допомогою рівняння (3.17) характеризується з точки зору керуючого впливу, а рівняння (3.16) відповідає обурючому впливу.

В раховуючи вищесказане, структурна схема керування електроприводом представлена двома паралельними каналами після керуючого впливу: струмового і швидкісного. Ці канали повністю відповідають структурним схемам, показаним на рис.3.2 і рис.3.4.

Рис. 3.5. Структурна схема ЕМС, регульованої за електромеханічною потужністю (електропривід потужності)

Завдання на виконання роботи.

1. В якості базової основи для виконання математичного експерименту прийняти модель двигуна постійного струму з незалежним збудженням (3.4).

2. Для даного типу двигуна розрахувати його параметри и представити у виді таблиці за прикладом (див. табл.3.1), параметри двигунів відповідних серій отримати із довідкової літератури (Копылов И.П. Справочник по електричним машинам).

3. Побудувати три структурні схеми системи управління електродвигуном. Принцип управління САУ - по відхиленню. Перша структурна схема - електропривод, регульований по швидкості обертання двигуна. Друга - електропривод, регульований по електромагнітному моменту на валу двигуна. Третя - електропривод, регульований по електромеханічної потужності двигуна. В якості закону регулювання можна вибрати ПІ-регулятор з лінійним коефіцієнтом посилення тиристорного перетворювача. Обурюючий вплив (момент навантаження) задати у вигляді східчастої функції (стрибок) з відповідним значенням.

3. Провести моделювання структурних схем за допомогою пакета прикладних програм Mlab_Simulink. Отримати перехідні характеристики швидкості обертання двигуна, електромагнітного моменту на валу двигуна і електромеханічної потужності двигуна для кожної САУ. Проаналізувати перехідні характеристики САУ систем за показниками якості, а також встановити час відпрацьовування регулятором збурюючого впливу на систему.

Таблиця 3.1-

Параметри математичної моделі електроприводу

Номінальні параметри електродвигуна 4ПНМ 160LГ	Потужність,	11 кВт
	Струм якорю	57 А
	Електромагнітна постійна двигуна, С	1,316 Вс
	Електромагнітний момент,	75 Нм
	Напруга,	220 В
	Число оборотів,	1400 об/мин
	Коефіцієнт передачі тахогенератора,	0,191 Вс/рад
	Коефіцієнт передачі датчика струму,	0,06 В/А
	Коефіцієнт посилення нормуючих підсилювачів, ,	0,36; 2,21
	Коефіцієнт перемножителя,	0,1 1/В
	Активний опір якоря,	0,139 Ом
	Індуктивність якоря,	0,001Гн
	Момент інерції, приведений до валу дви-гунів,	0,2 кг м2
Електромеханічні параметри двигуна	Електромагнітна постійна часу,	0,007 с
	Електромеханічна постійна часу,	0,02 с
	Коефіцієнт демпфування, 	0,7
Параметри ПІ-регулятора	Коефіцієнт пропорційної складової, К	5
	Постійна часу,	0,01 с

Серії двигунів обрати за варіантами:

1	4ПО80А1	11	4ПБ80В1	5	4ПФ132М	15	4ПБ1001Л
2	4ПО80А2	12	4ПФ180М	6	4ITO100L1	16	4ПБ112М1
3	4ПО80В1	13	4ПФ160М	7	4ПО112М1	17	4ПБ112М2
4	4ПФ1328	14	4ПБ10082	8	4ПО112М2	18	4ПФ112М