35

Міністерство освіти і науки, молоді та спорту України

ДВНЗ «Донецький Національний Технічний Університет»

Кафедра Автоматики та телекомунікацій

Методичні вказівки до виконання лабораторних робіт

по курсу: "Математичні моделі об’єктів та систем автоматизації" (частина ІІ)

для бакалаврів денної та заочної форм навчання за напрямом 6.050201 «Системна інженерія»

розглянуто на засіданні кафедри

автоматики і телекомунікацій.

протокол № 2

від «28» лютого 2013 р.

затверджено на засіданні

науково-видавничої ради ДонНТУ

протокол № ___

від «___» ___________ 2013 р.

Донецьк, ДонНТУ 2013

УДК 681.3.

Методичні вказівки до лабораторних робіт по курсу "Математичні моделі об’єктів та систем автоматизації" (частина ІІ) для бакалаврів денної та заочної форм навчання за напрямом 6.050201 «Системна інженерія»/ доц. Жукова Н.В. - Донецьк, ДонНТУ. 2013 рік. -37 с.

Методичні вказівки містять лабораторні роботи з основних розділів курсу " Математичні моделі об’єктів та систем автоматизації " (частина ІІ) і призначені для бакалаврів денної та заочної форм навчання за напрямом 6.050201 «Системна інженерія».

Укладач доц. Жукова Н.В.

Рецензент доц. Ф-ту КНТ каф. АСУ Cвітлична В.А.

доц. Ф-ту КІТА каф. ЕТ Тарасюк В.П.

Відповідальний за випуск проф. Турупалов В.В.

Зміст

1. Лабораторна робота №1.

Способи опису лінійних динамічних систем. (частина 1)…………………………

2. Лабораторна робота №2.

Способи опису лінійних динамічних систем. (частина 2)……………….………..

3. Лабораторна робота №3.

Розробка та аналіз структурних схем САУ електроприводом постійного струму з незалежним збудженням……………………………………………………….…..

4. Лабораторна робота №4.

Синтез лінійних стаціонарних систем засобами SISO Design Tool……………….

Лабораторна робота №1

Тема: Способи опису лінійних динамічних систем. (частина 1)

Мета роботи: Отримати навички опису фізичних систем за допомогою передавальних функцій і в просторі станів, отримати навички роботи в Matlab - Simulink при моделюванні динаміки САУ.

Теоретичні відомості.

Способи опису лінійних динамічних систем.

У пакеті розширення Control System Toolbox системи MATLAB прийняті наступні способи опису лінійних динамічних систем з постійними параметрами: система рівнянь першого порядку в фазовому просторі, або в просторі станів системи (ss — state-space), передатна функція системи у вигляді відношення двох поліномів (tf), передатна функція в так званому вигляді нуль / полюс / коефіцієнт підсилення (zpk). Найбільшого поширення набув перший спосіб, який дає найкращу точність при обчисленнях і більшою мірою зручний при теоретичних дослідженнях і практичній реалізації алгоритмів керування з застосуванням обчислювальних машин і т. д.

Методи фазових координат (в просторі стану). При застосуванні цього способу диференціальні рівняння, що описують динаміку системи, мають вигляд:

, (1.1)

де - n - мірний вектор стану системи (вектор фазових координат), - m - мірний вектор зовнішніх впливів, що складається із заданих величин, збурень, управлінь, які формуються регулятором, А і В - перехідна матриця системи і матриця керування відповідних розмірів. Передбачається, що вимірюванню доступна тільки частина станів системи або їх лінійних комбінацій, такі змінні у називаються виходами системи:

, (1.2)

де y – r - мірний вихідний вектор, С, D - матриці відповідних розмірів. Для більшості реальних об'єктів управління D = 0.

У розглянутих пакетах розширення є можливість маніпулювати з системою, що описується рівняннями (1.1), (1.2), як з одним об'єктом MATLAB. Для цього потрібно матриці А, В, С, D трансформувати в систему, використовуючи команди ss із Control System Toolbox.

Розглянемо як приклад обертову механічну систему, що складається з двох інерційних мас і з'єднаних пружною муфтою (рис. 1.1).

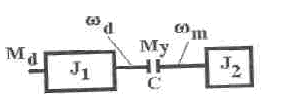
Рис. 1.1. Механічна система з еластичною муфтою

Момент, який передається муфтою, який є моментом опору для першої інерційної маси і рушійним моментом для другої, пропорційний різниці кутових переміщень обох мас з коефіцієнтом пропорційності С. Управлінням є приводний момент першої маси (зазвичай момент приводного двигуна), а виходом - швидкість її обертання, так як на валу приводного двигуна зазвичай встановлюється датчик швидкості. Для простоти момент опору вважаємо рівним нулю. Рівняння системи буде таким:

; (1.3)

, тоді ; (1.4)

. (1.5)

Перепишемо ці рівняння в систему Коші:

(*)

Якщо позначити, , , то розглянуту систему (*) можна записати в векторно-матричному вигляді (1.1), (1.2):

, ,

де

Тепер створимо систему, використовуючи команди ss. Створимо m-файл (П. 1.1). Параметри прикладу взято для обертової печі цементного виробництва. В командному вікні МАТLAB відкриємо послідовно вікна File, New, М-файл і введемо текст (звичайно, коментар можна не вводити):

Clear % очищення робочої області пам'яті

Clc % очищення робочого вікна

J1=21.5;J2=7;C=243;% введення параметрів

a=[0 -1/J1 0;C 0 -C;0 1/J2 0];% створення матриці А (П. 1.1)

b=[1/J1;0;0];c=[1 0 0];d=0;% створення матриць B, C, D

sys1=ss(a,b,c,d)% формування системи для системи управління Toolbox

Відзначимо наступне: матриці можна вводити як одну текстову рядок, причому рядки матриці відокремлюються один від одного крапкою з комою, а окремі елементи рядка матриці розділяються пробілами. Якщо необхідна довжина текстового рядка перевищує ширину сторінки, то можна переносити її на наступний рядок, причому в місці розриву повинні бути поставлені крапки не менше трьох. Якщо після команди є крапка з комою, то результати виконання команди в командному вікні не з'являються. Якщо виконати цю програму (у вікні редактора виконати Debug і Run або зберегти і запустити), то результат запам'ятовується в робочій області (Workspace). Якщо тепер відкрити її (у вікні MATLAB виконати робочий стіл, потім Workspace), то з'явиться утримання робочої: серед інших об'єктів буде sysl. Якщо тепер розкрити цю систему шляхом подвійного натискання лівої клавіші миші, то буде видно, що система являє собою зібрання матриць а, b, с, d. При розгляді sysl видно, що змінні мають типові позначення, xl, x2 і т. д., завжди бажано мати імена відображають фізичну суть величин. Додамо команду:

set(sys1,'StateName',{'Wd';'My';'Wm'},'InputName','Md','OutputName','Wd')

і виконаємо програму, розкриємо робочу область, розкриємо sysl і побачимо, що тепер змінні мають потрібні імена.

Уже у вигляді (1.1), (1.2), нас може цікавити ряд характеристик системи. У першу чергу, чи є система стійкою і як розташовуються її полюса, т. е. коріння характеристичного рівняння. Скористаємося командою:

Pa=eig(a)

отримаємо Pa =0; 0 + 6.7836i; 0 - 6.7836i, т. е. всі три корені розташовані на уявної осі (i - знак уявної одиниці).

Для того щоб системою можна було нормально керувати, вона повинна, як правило, бути керованою і спостережливою. Система є повністю керованою, якщо її можна з будь-якого початкового стану привести в нульовий стан за кінцевий час, використовуючи довільно простір управлінь. Нехай, наприклад, в системі одне з рівнянь має вигляд , тоді очевидно, що на процес зміни впливати можна, т. е. система є некерованою. Система є повністю спостерігається, якщо за спостереженнями протягом кінцевого часу за її виходом можна визначити початковий стан системи. Нехай в системі третього порядку друге рівняння має вигляд: , причому координата не входить ні в рівняння для , , ні в вираз для у. Таким чином, координата не «проявляє» себе на виході системи ні безпосередньо, ні через інші координати, і система виявляється неспостережливою.

Для керованості системи потрібно, щоб матриця керованості:

(1.7)

мала ранг п. Нагадаємо, що ранг матриці дорівнює порядку найбільшого визначника матриці, відмінного від нуля, за умови, що всі старші визначники рівні нулю. Відповідно для спостережливості системи потрібно, щоб матриця спостережливості:

(1.8)

мала ранг п. Для перевірки керованості і спостережливості нашої системи доповнимо програму (П.1.1) командами:

Ccon=ctrb(a,b)

Unco=length(a)-rank(Ccon)

Cob=obsv(sys1)

Unob=length(a)-rank(Cob)

Перша і третя команди формують матриці керованості і спостережливості, а друга та четверта обчислюють різниці між рангом цих матриць і порядком системи. Після виконання нашої програми отримаємо в командному вікні Unco=0, Unob=0, тобто наша система повністю керована і спостережлива. Звернемо увагу, що аргументом цих команд можуть бути як вхідні матриці системні матриці (перша команда), так і сама система (третя команда).

Розглянуті системи в загальному випадку мають кілька входів і виходів і відносяться до так званих систем MIMO (кілька входів - багато виходів). Приватним, але досить поширеним на практиці є випадок систем з одним входом і одним виходом (SISO системи). Методи аналізу і синтезу MIMO систем можуть бути застосовані до SISO систем, однак останні простіші, і для роботи з ними можуть бути використані спеціальні методи.

Для системи (1.1), (1.2) іноді використовується позначення:

(1.9)

Це означає, що система описується рівняннями системи (1.1), (1.2.). Часто також у системі вхідні і вихідні змінні розділяються: входи - на зовнішні впливи і регулюючі (керуючі) сигнали , виходи - на регульовані (керовані) та вимірювані . При цьому рівняння системи набувають вигляду:

(1.10)

(1.11)

(1.12)

Система в такому вигляді позначається як

(1.13)

Передбачається, що регулятор на підставі вимірів виробляє сигнал таким чином, що вихід при заданому має бажані властивості (рис. 1.2).

Рис. 1.2. Структурна схема системи з розділеними входами і виходами

Врахуємо в даній системі (1.3) - (1.6) момент навантаження і припустимо, що мета регулювання - зменшити відхилення швидкості механізму при дії . Запишемо (1.5) як

(1.14)

і позначимо , . Тоді отримаємо систему (1.13) при всіх .

,

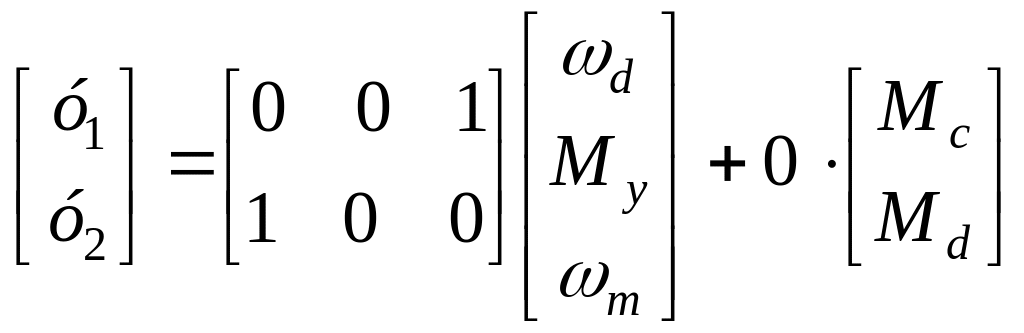де (1.15)

Приклад виконання. Розглянемо приклад. Привід маси, що обертається (рис. 1.1) здійснюється від двигуна, що має момент інерції , через еластичну муфту з коефіцієнтами жорсткості , що створює на валу двигуна пружний момент М_у. Електромагнітний момент двигуна дорівнює добутку струму якоря на постійну машини , швидкість обертання двигуна . Маса, що обертається має момент інерції і швидкість обертання . Всі величини приведені до швидкості обертання вала двигуна. Пружний момент пропорційний різниці кутових положень вала двигуна і маси, що обертається. Регулювання обертання швидкості двигуна, який приводить в рух механізм, здійснюється ПІ-регулятором, на вході якого порівнюються два сигнали: сигнал завдання швидкості обертання і сигнал зворотного зв'язку швидкості двигуна. Мета управління - стабілізація швидкості обертання механізму.

Математична модель замкнутої системи з ПІ-регулятором в інтегро - диференціальної формі має вигляд.

(1.16)

Н а підставі даної системи рівнянь побудуємо структурну схему замкнутої САУ (рис. 1.7).

Рис.1.7. Структурна схема замкнутої САУ швидкістю обертання механізму

Результати моделювання замкнутої системи наведені на рис. 1.8.

Рис.1.8. Перехідні характеристики замкнутої САУ швидкістю обертання механізму

Завдання на виконання роботи.

Варіант 1.

Для об'єкта, зображеного на рис.1.3 з постійною двигуна С=5; моментом інерції двигуна і вентиля J=0.005 кг·м², опором R=10 Ом; площею перерізу бака S=45 м², витратою і витратою на виході побудувати систему управління рівнем води в баку.

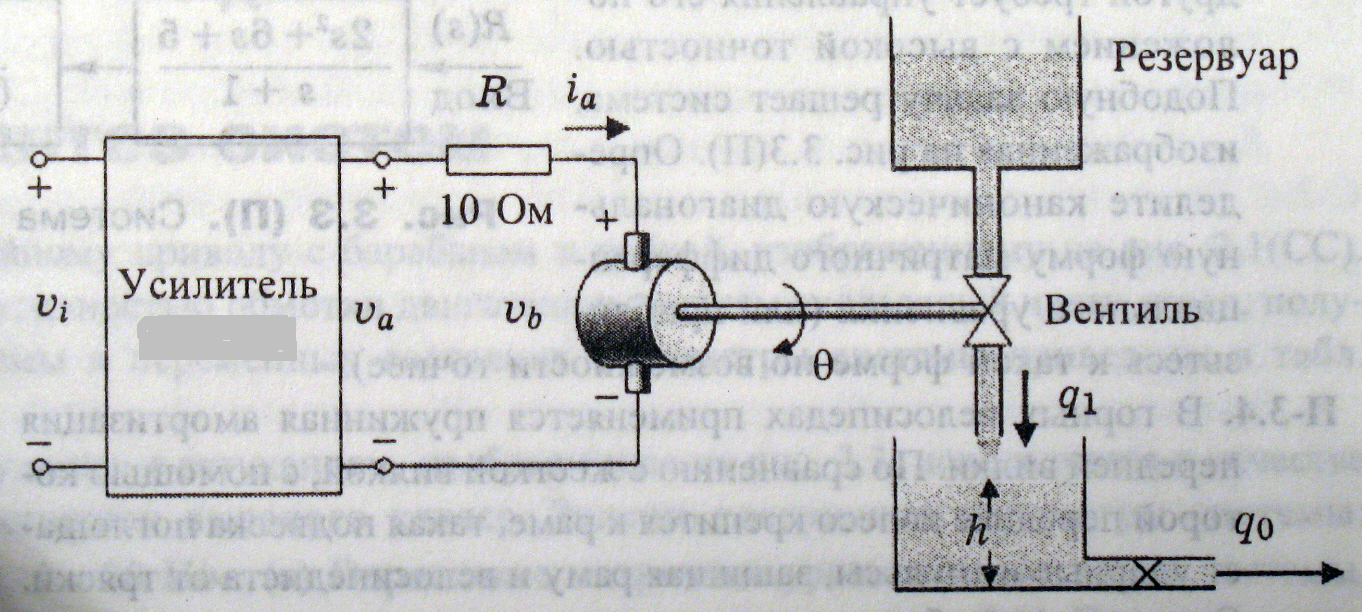
Рис.1.3 – Система регулювання рівнем води в баку

Двигун постійного струму, швидкість обертання якого визначається струмом якоря , змінює ступінь відкриття вентиля. Для спрощення математичного опису індуктивністю якірної обмотки двигуна, а також коефіцієнтом тертя при обертанні його вала і вентиля можна знехтувати. Рівень води в баку визначається рівнянням: .

1.Получіть математичний опис замкнутої системи управління у вигляді системи інтегро - диференціальних рівнянь. В якості закону управління прийняти ПІ-закон.

2. Отримати рішення в перетвореннях Лапласа за основними регульованими змінними: струм якоря швидкість обертання двигуна , кут повороту вентиля , рівень води в баку , а також керуючого впливу на двигун .

3. Побудувати структурну схему замкнутої САУ рівнем води в баку використовуючи рішення отримані в п.2.

3. За допомогою пакета Matlab-Simulink:

- побудувати схему моделювання замкнутої САУ рівнем води в баку;

- поставити настроювальні параметри ПІ-регулятора та отримати перехідні характеристики за основними регульованим змінними (швидкість обертання двигуна, кут повороту вентиля, рівень води в баку). Перехідний процес за рівнем повинен бути аперіодичним з можливим перерегулюванням (20 ... 30%);

- проаналізувати динаміку САУ.

Варіант 2.

Привід маси, що обертається (рис. 1.4) здійснюється від двигуна, що має момент інерції , через пружну зв'язок з коефіцієнтами жорсткості , що створює на валу двигуна пружний момент .

Рис. 1.4. Механічна система з пружною зв'язком

Швидкість обертання двигуна , кут повороту . Обертова маса має момент інерції , швидкість обертання і кут повороту . Всі величини приведені до швидкості обертання вала двигуна. Пружний момент пропорційний різниці кутових положень вала двигуна і маси, що обертається маси. У даній системі (рис. 1.4) враховується момент навантаження і передбачається, що мета регулювання - стабілізація кутового положення механізму при дії . Регулювання кутового положення обертового механізму, здійснюється ПІ-регулятором.

Для спрощення математичного опису індуктивністю якірної обмотки двигуна, а також коефіцієнтами тертя при обертанні вала двигуна і механізму можна знехтувати.

Параметри об'єкта і двигуна: постійна двигуна С=1,32; опір якоря двигуна R=0139 Ом, моменти інерції J1=7 кг·м², J2=21,5 кг·м², коефіцієнт жорсткості =243.

1.Получіть математичний опис замкнутої системи управління у вигляді системи інтегро - диференціальних рівнянь. В якості закону управління прийняти ПІ-закон.

2. Отримати рішення в перетвореннях Лапласа за основними регульованим змінними: швидкість обертання двигуна , кут повороту , швидкість обертання механізму і кут повороту , момент пружного зв'язку , а також керуючого впливу на двигун .

3. Побудувати структурну схему замкнутої САУ кутовим положенням використовуючи рішення отримані в п.2.

3. За допомогою пакета Matlab-Simulink:

- побудувати схему моделювання замкнутої САУ кутовим положенням;

- підібрати настроювальні параметри ПІ-регулятора та отримати перехідні характеристики за основними регульованими змінними (швидкість обертання двигуна, кут повороту, швидкість обертання механізму, кут повороту, момент пружною зв'язку). Перехідний процес за кутовим положенням повинен бути аперіодичним з можливим перерегулюванням (20 ... 30%). Обурюючий вплив задати у вигляді ступеневої функції в нульовий момент часу (величину обрати близько 10-15 Нм);

- промоделюйте ступінчастий накид в сталому режимі і зробіть висновок про час відновлення вихідної змінної (кутового переміщення) після ступеневої накиду навантаження.

Варіант 3

Система читання інформації з диска. Мета управління - позиціонування голівки, що зчитує на певній доріжці диска. Регульована змінна - положення г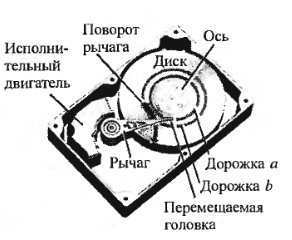 олівки , що зчитує, закріпленої на кінці важеля. Диск обертається зі швидкістю від 1800 до 7200 об/хв, а головка плаває над диском на відстані менше 100 нм. Вимога до точності позиціонування 1 мкм. Переміщення головки від доріжки до доріжки повинно відбуватися не більше, ніж за 0,5 с.

О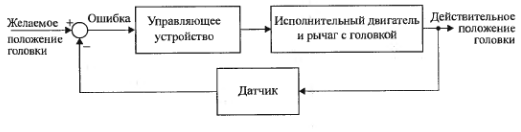 брати принцип керування системи - управління по відхиленню (рис.1.5).

Рис.1.5 - Замкнута система управління дисководом

О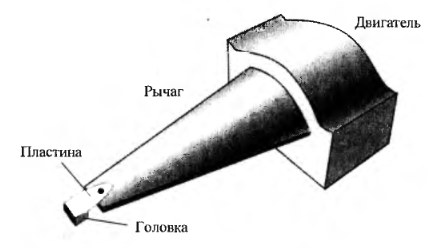 скільки для швидкого переміщення головки необхідно мати малу масу важеля, то необхідно врахувати вигин пластини, виготовленої пружною сталевої стрічки.

Т оді модель пристрою, що зчитує необхідно представити як модель з двома масами і пружною пластиною (рис.1.6). Сила, яка веде в рух масу М₁, створюється двигуном постійного струму, тобто активним моментом М_d.

Рис.1.6 - Модель пристрою, що зчитує

Параметри об'єкта та двигуна:

- постійна двигуна С = 5 Нм/А; - опір якоря R = 1 Ом;

- індуктивність якоря 1мГн; - момент інерції J_d = 1 кг•м²;

- маса двигуна М₁ = 0,02 кг; - маса головки М₂ = 0,0005 кг;

- коефіцієнт пружності пластини ;

- коефіцієнт тертя маси b₁ = 410E-3 Кг/м/ с;

- коефіцієнт тертя маси b₂ = 4.1e-3 Кг/м/с;

1.Получіть математичний опис замкнутої системи управління у вигляді системи інтегро - диференціальних рівнянь. В якості закону управління прийняти П-закон.

2. Отримати рішення в перетвореннях Лапласа за основними регульованими змінними: струм якоря i(t), швидкість обертання двигуна , кут повороту , і переміщення головки , а також керуючого впливу на двигун . Вираз для обурючого впливу на двигун має бути отримано виходячи з моделі рис.1.6.

3. Побудувати структурну схему замкнутої САУ положенням головки використовуючи рішення отримані в п.2.

3. За допомогою пакета Matlab-Simulink:

- побудувати схему моделювання замкнутої САУ становищем головки;

- підібрати настроювальні параметри П - регулятора та отримати перехідні характеристики за регульованою змінної. Перехідний процес бути аперіодичним з можливим перерегулюванням (1 ... 3%).

Контрольні питання.

1. Перерахувати способи опису ЛДС.

2. У чому полягає спосіб опису ДС в фазовому просторі?

3. У чому полягає спосіб опису ДС допомогою ПФ?

4. У чому полягає спосіб опису ДС в так званому вигляді нуль / полюс / коефіцієнт підсилення (ЗПК)?

5. Що таке MIMO системи? Для замкнутої системи з розділеними входами і виходами (у загальному вигляді) напишіть рівняння динаміки і виходів.

6. Перерахувати загальні властивості моделей систем.

7. Перерахувати команди з'єднання моделей.

8. Отримати математичну модель у просторі станів замкнутої САУ, порівняти з результатами моделювання структурної схеми САУ в Simulink і САУ з підсистем.