
Проведение расчетов
Для расчетов используется математический пакет MathCad PLUS 5.
- этот оператор устанавливает номер первого элемента вектора (по умолчанию он равен нулю)
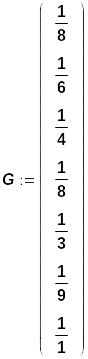
Для ввода векторов необходимо после оператора присвоения ":=" вызвать диалоговое окно "Matrices" путем комбинации клавиш Ctrl+M,
Затем в полях ввода установить 7 строк и 1 столбец и мышкой "нажать" кнопку "Create". После этого появляется шаблон с незаполненными элементами вектора. Для заполнения достаточно вводить числа (1/R) и для перехода к следующему элементу щелкать мышкой в нужном месте.
Теперь можно задать матрицу коэффициентов при неизвестных системы узловых уравнений и вектор правых частей
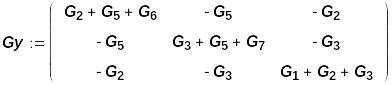
Индексы вводятся после нажатия открывающей квадратной скобки [
Для ввода слагаемых с индексом нужно после ввода индекса нажать на клавишу "Пробел", а затем на "+"
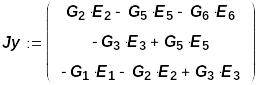
Решение системы уравнений
![]()
Для вывода решения нужно просто написать Uy =
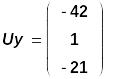
Зная узловые напряжения, можно определить токи в ветвях:
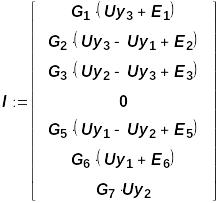
Напряжения R - элементов определяются по закону Ома
- счетчик с шагом 1. Вводится так: k Shift+; 1 ; 7 Enter
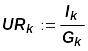
Напряжения ветвей определяются по узловым напряжениям

Напряжение четвертой ветви, в которой нет тока, определяется только напряжением источника Е4.
Замечание: на исходной схеме точка "" с нулевым потенциалом находится на ветви 4, поэтому потенциалы всех остальных узлов ОТНОСИТЕЛЬНО точки "" равны:
 ,
В.
,
В.
Потенциал четвертого – опорного узла равен: 0 – (–100) = 100 В.
Правильность расчетов можно проверить, составив баланс мощностей:
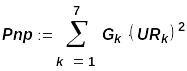
Для ввода оператора суммы необходимо на панели инструментов (слева у обреза экрана) нажать мышкой соответствующую кнопку.
Мощность всех источников цепи равна:
Баланс мощностей выполнен, значит, расчеты верны.
МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
Этот метод широко используется для расчета и анализа цепей, когда интересуются током или напряжением в одной ветви или в одном элементе. Например, когда нужно определить, как влияет параметр элемента ветви на режим работы цепи.
Суть метода заключается в представлении цепи, состоящей из двух частей: элемента, для которого определяется ток или напряжение, и остальной цепи в виде эквивалентного генератора – источника напряжения с параметрами EЭКВ и RЭКВ или – источника тока с параметрами JЭКВ и GЭКВ. При этом ток определяется по формуле:
![]() , (2.7)
, (2.7)
а напряжение: ![]() .
(2.8)
.
(2.8)
В качестве примера определим напряжение
UR2
в цепи рис. 2.3 в зависимости от сопротивления
R4.
качестве примера определим напряжение
UR2
в цепи рис. 2.3 в зависимости от сопротивления
R4.
На рис. 2.4, а приведена эта схема, где ветвь с R2 подключена к остальной цепи в двух узлах 1 и 2. Вся цепь относительно выделенной ветви с R2 представляется источником напряжения с внутренним сопротивлением RЭКВ и ЭДС источника ЕЭКВ рис. 2.4, б. Эквивалентное– внутреннее сопротивление источника равно входному сопротивлению цепи относительно зажимов 1– 2.

а) б)
в) г)
Схема на рис. 2.4, в, получена из схемы рис. 2.4, а при нулевых напряжениях источников напряжения и нулевом токе источника тока. В этой цепи R3 и R4 оказываются соединены параллельно. Заменив их одним эквивалентным элементом с сопротивлением R34, получим последовательно соединенные R34 и R1, которые тоже заменим одним эквивалентным RВХ . Итак,
![]() .
.
Эквивалентный источник напряжения имеет ЭДС, равную напряжению холостого хода (при разомкнутой ветви с R2). Схема для определения этого напряжения приведена на рис. 2.4, г.
Напряжение U2ХХ можно найти по закону Кирхгофа для напряжений:
UXX = –E2+ U'1+ U'3,
где
U'1 =
R1J1,
![]() .
Теперь для цепи рис. 2.4, б можно
записать:
.
Теперь для цепи рис. 2.4, б можно
записать:
 .
.
Полученное
соотношение можно исследовать аналитически
или численно при различных значениях
параметров элементов. Например, можно
найти значения R4,
при которых I2 = 0.
Для определения UR2
можно воспользоваться законом
Ома
![]() и проанализировать влияние R4
на UR2.
Поставленная задача решена.
и проанализировать влияние R4
на UR2.
Поставленная задача решена.
ОСНОВЫ СИМВОЛИЧЕСКОГО МЕТОДА РАСЧЕТА. РАСЧЕТ ЦЕПЕЙ С ОДНИМ ИСТОЧНИКОМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Все расчеты цепей выполняются в пакете MathCad
ЗАДАЧА 1
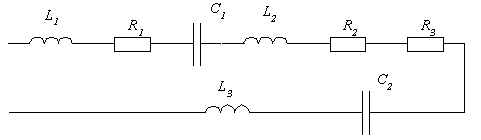
Исходные данные для расчета:
![]() Гц;
Гц;
![]() Гн;
Гн;
![]() Ом;
Ом;
![]() Ф;
Ф;
![]() Гн;
Гн;
![]() Ом;
Ом;
![]() Ф;
Ф;
![]() Гн;
Гн;
![]() Ом;
Ом;
Индексы вводятся нажатием клавиши [ – открывающая квадратная скобка.
Требуется определить полное сопротивление цепи, активное и реактивное сопротивления, а также представить эквивалентную схему цепи, рассчитав параметры ее элементов.
РЕШЕНИЕ
Представляем комплексную схему замещения цепи
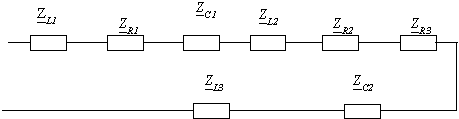
Здесь для индуктивных элементов: ZL = jxL = jL, для резистивных элементов ZR = R,
для емкостных элементов ZС = – jxC = 1 /(jС).
Поскольку все элементы соединены последовательно, то их общее эквивалентное комплексное сопротивление равно сумме комплексных сопротивлений элементов.
Zo = ZL1 + ZR1 + ZC1 +ZL2 + ZR2 + ZR3 +ZC2 + ZL3 =
= (R1 + R2 + R3) + j(L1 + L2 + L3 – 1/C1 – 1/C2) = Ro + jXo
Общее активное сопротивление Rо равно
![]()
![]() Ом;
Ом;
![]() Для
ввода греческого символа :
w и
затем
Ctrl+G
Для
ввода греческого символа :
w и
затем
Ctrl+G
Общее реактивное сопротивление Xо (может быть отрицательным) равно:
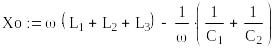
![]() Ом;
Ом;
О бщее
полное сопротивление Zо
равно
бщее
полное сопротивление Zо
равно
![]()
![]() Ом;
Ом;
Для ввода корня квадратного нажать клавишу " \ " (Слеш) – находится справа от клавиши =
Поскольку общее реактивное сопротивление положительно, то эквивалентная схема замещения цепи (вся цепь может быть представлена R-L-элементами) имеет вид:
Здесь
Ом; 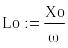
![]() Гн.
Гн.
Самостоятельные расчеты для частоты 50 Гц.
![]() Гц;
Гц;
Общее активное сопротивление Rо равно
Ом;
Общее реактивное сопротивление Xо равно:
![]() Ом;
Ом;
О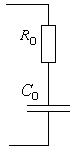 бщее
полное сопротивление Zо
равно
бщее
полное сопротивление Zо
равно
![]() Ом;
Ом;
Длa ввода квадратного корня нажать клавишу " \ " (Слеш)
Поскольку общее реактивное сопротивление отрицательно, то эквивалентная схема замещения цепи имеет вид, показанный слева.
Здесь
Ом; 
![]() мкФ.
мкФ.
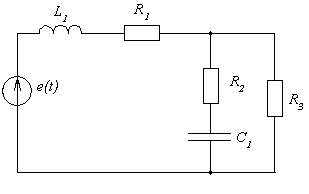
ЗАДАЧА 2
Рассчитать токи всех элементов, если напряжение источника промышленной частоты составляет 220 В; параметры остальных элементов:
L1 := 0,114 (Гн)
R1 := 8 (Ом)
С1 := 15010–6 (Ф)
R2 := 11 (Ом)
R3 := 9,6 (Ом).
![]() -
задание мнимой единицы
-
задание мнимой единицы
Комплексная амплитуда напряжения источника:
![]()
Обычно задано
действующее напряжение, поэтому для
расчета амплитуды введен множитель
![]() ,
начальная фаза принята нулевой, поскольку
в условии она не задана.
,
начальная фаза принята нулевой, поскольку
в условии она не задана.
Чтобы в дальнейшем на рабочем листе обозначение мнимой единицы было "j", а не "i", нужно в меню Math выбрать команду Numerical Format ... и установить мышкой переключатель с обозначением мнимой единицы j
Круговая частота источника напряжения:
f := 50 (Гц).
Угловая частота источника напряжения:
:=
2
f ![]() (рад/с).
(рад/с).
Комплексные сопротивления ветвей:
![]()
![]() (Ом);
(Ом);
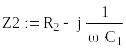
![]() (Ом);
(Ом);
![]()
![]() (Ом).
(Ом).
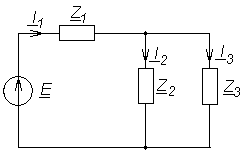
Расчет выполним с помощью эквивалентных преобразований цепи. Заменим параллельно соединенные элементы Z2 и Z3 одним Z23:
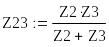
![]() (Ом).
(Ом).
Заменим последовательно соединенные элементы Z1 и Z23 одним Z0:
![]()
![]() (Ом);
(Ом);
Теперь можно рассчитать комплексную амплитуду тока в первой ветви:
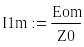
![]() (А).
(А).
Комплексная амплитуда напряжения на элементе Z23:
![]()
![]() (В).
(В).
Комплексная амплитуда тока второй ветви
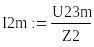
![]() (А).
(А).
Комплексная амплитуда тока третьей ветви
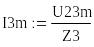
![]() (А).
(А).
В пакете MathCad комплексные числа рассчитываются и представляются на рабочем листе в алгебраической форме записи, поэтому для перевода комплексных токов в синусоидальные функции необходимо представить комплексные числа в показательной форме. Для этого следует определить модули и аргументы комплексных чисел с помощью операторов | | – модуль и arg() – аргумент:
![]() (А).
(А).
Для ввода операции модуля: I 1 m Shift + | (символ вертикальной черты, находящийся справа от клавиши =)
![]() (А);
(А);
![]() (А).
(А).
![]() (рад);
(рад);
![]() (рад);
(рад);
![]() (рад).
(рад).
Токи в функции времени – мгновенные значения токов имеют вид:
![]()
![]()
![]()
Напряжение источника в функции времени – мгновенное значение
![]()
Теперь можно построить графики тока и напряжения источника. Для построения графиков необходимо задать "дискретные значения аргументов".
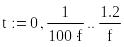
Порядок ввода: t Shift+; 0 , 1 / 100 * f пробел ; 1 . 2 / f и Enter
Затем вызывается шаблон двумерного графика с помощью комбинации клавиш Shift + 2
Затем в нижнем среднем квадратике вводится аргумент функций - время t, а в среднем слева квадратике вводится функция напряжения eo(t) и нажимается клавиша , (запятая) и вводится функция тока i1(t). После нажатия клавиши Enter появится графики
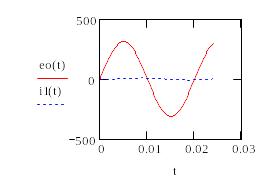
Mathcad строит математические, а не физические зависимости, поэтому единица напряжения и единица тока имеют одинаковые масштабы. Поэтому чтобы увидеть кривую тока, необходимо увеличить ток, например, в 40 раз. Для этого нужно кликнуть мышкой на i1(t) слева от графиков. Если появится текстовый курсор | , то дважды нажать на стрелку вверх (клавиша управления курсором), чтобы i1(t) заключился в синюю рамку. Если сразу после клика мышкой i1(t) будет заключен в синюю рамку, то затем нажать на клавиши умножения (*) 4 0 и Enter
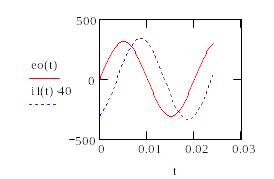
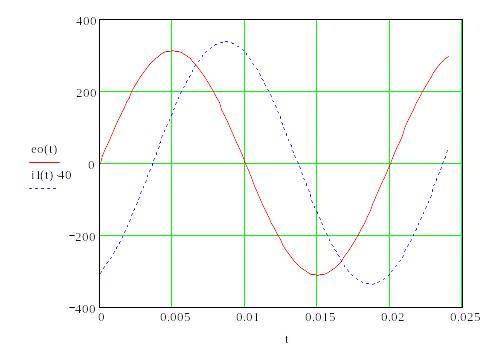
Можно увеличить рисунок, потянув мышкой правый нижний угол пунктирной рамки вокруг графика. Пунктирная рамка возникает, если рядом с графиком нажать левую клавишу мыши и, не отпуская ее, потянуть курсор мыши к рисунку.
Для проверки правильности расчетов составляется баланс мощностей. Для этого рассчитывается комплексная мощность источника
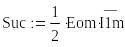
![]() (ВА).
(ВА).
Для ввода комплексного сопряженного числа (обозначено чертой над током) нужно после ввода I 1 m нажать клавишу " (Shift+ ' )
Множитель ½ вводится для того, чтобы учесть амплитуды, а не действующие значения тока и напряжения.
Активная мощность приемников
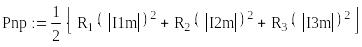
![]() (Вт).
(Вт).
Реактивная мощность приемников
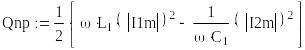
![]() (вар).
(вар).
Видно, что баланс мощностей выполнен, поэтому расчеты верны.
ИССЛЕДОВАНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА /Лабораторно-практическое занятие
ЦЕЛЬ РАБОТЫ
Исследовать разветвленную электрическую цепь с одним источником синусоидального напряжения. Научиться рассчитывать токи и напряжения символическим методом, научиться определять параметры пассивных двухполюсников типа R-C и R-L методом трех вольтметров.
Практическое занятие РАСЧЕТ ПАССИВНЫХ ДВУХПОЛЮСНИКОВ
Теоретические сведения "Последовательное соединение элементов"
Расчет пассивных двухполюсников состоит в расчете параметров элементов, входящих в двухполюсник.
Возможные схемы пассивных двухполюсников приведены на рис. 4.1.

Схема двухполюсника определяется током и напряжением на зажимах. Пусть синусоидальные ток и напряжение равны:
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
Здесь обозначено: Im – амплитуда тока, Um – амплитуда напряжения, U – действующее напряжение, I – действующий ток, – угловая частота изменения тока (напряжения), i – начальная фаза тока, u – начальная фаза напряжения.
Действующие напряжение и ток – величины, которые обычно измеряют с помощью вольтметра и амперметра.
Угловая частота
связана с круговой частотой f
и периодом T
соотношением: ![]() (4.3)
(4.3)
Сопротивлением
двухполюсника называют полное
сопротивление, рассчитываемое по
формуле: ![]() (4.4)
(4.4)
Фазовый сдвиг или
сдвиг по фазе между напряжением и током
определяется формулой
![]() ,
и для любого пассивного двухполюсника
лежит в пределах:
,
и для любого пассивного двухполюсника
лежит в пределах:
![]() (–1
sin
1, 0
cos
1).
(–1
sin
1, 0
cos
1).
Активным сопротивлением двухполюсника называется величина:
![]() . (4.5)
. (4.5)
Это значит, что активное сопротивление R не может быть отрицательным.
Реактивным сопротивлением двухполюсника называется величина:
![]() . (4.6)
. (4.6)
Это значит, что реактивное сопротивление Х может быть как положительным, так и отрицательным, а также может быть равным нулю.
Полное сопротивление
связано с активным и реактивным очевидным
соотношением:
![]() .
.
1Если
![]() ,
то
,
то
![]() и синусоида напряжения опережает
синусоиду тока, то есть синусоида
напряжения достигает максимума РАНЬШЕ,
чем максимума достигнет синусоида тока.
На рис. 4.2 показаны три случая, когда
напряжение опережает ток при различных
начальных фазах напряжения.
и синусоида напряжения опережает
синусоиду тока, то есть синусоида
напряжения достигает максимума РАНЬШЕ,
чем максимума достигнет синусоида тока.
На рис. 4.2 показаны три случая, когда
напряжение опережает ток при различных
начальных фазах напряжения.
Этот случай
соответствует сдвигу по фазе между
напряжением и током в цепи с последовательным
соединением резистивного и индуктивного
элементов (рис. 4.1,г).
При этом реактивное сопротивление равно
индуктивному сопротивлению: ![]()
2Если
![]() ,
то
,
то
![]() и синусоида напряжения отстает
от синусоиды тока, то есть синусоида
напряжения достигает максимума ПОЗЖЕ,
чем максимума достигнет синусоида тока.
Этот случай соответствует сдвигу по
фазе между напряжением и током в цепи
с последовательным соединением
резистивного и емкостного элементов
(рис. 4.1,в).
При этом реактивное сопротивление
равно емкостному сопротивлению,
взятому с обратным знаком:
и синусоида напряжения отстает
от синусоиды тока, то есть синусоида
напряжения достигает максимума ПОЗЖЕ,
чем максимума достигнет синусоида тока.
Этот случай соответствует сдвигу по
фазе между напряжением и током в цепи
с последовательным соединением
резистивного и емкостного элементов
(рис. 4.1,в).
При этом реактивное сопротивление
равно емкостному сопротивлению,
взятому с обратным знаком:
![]()
3Если
![]() ,
то
,
то
![]() и это значит, что синусоида напряжения
совпадает
по фазе с синусоидой тока, то есть
синусоида напряжения достигает максимума
ОДНОВРЕМЕННО с синусоидой тока. Этот
случай соответствует сдвигу по фазе
между напряжением и током в цепи с
резистивным элементом (рис.4.1,б).
При этом реактивное сопротивление равно
нулю:
и это значит, что синусоида напряжения
совпадает
по фазе с синусоидой тока, то есть
синусоида напряжения достигает максимума
ОДНОВРЕМЕННО с синусоидой тока. Этот
случай соответствует сдвигу по фазе
между напряжением и током в цепи с
резистивным элементом (рис.4.1,б).
При этом реактивное сопротивление равно
нулю:
![]()
Таким образом, независимо от величины напряжения и величины тока схема двухполюсника (рис. 4.1) определяется исключительно сдвигом по фазе между напряжением и током.
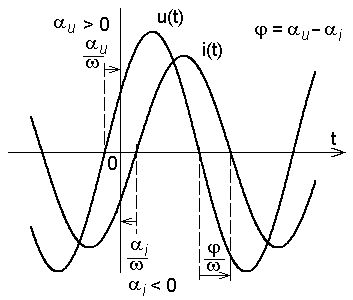
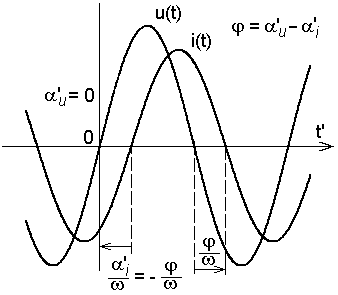
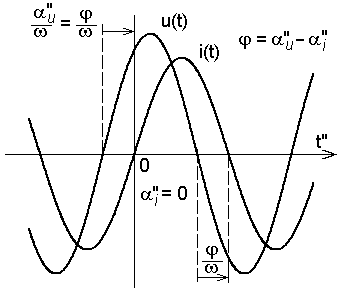
Рис. 4.2. Синусоида напряжения ОПЕРЕЖАЕТ
синусоиду тока
по фазе на угол
(по времени на
![]() )
)
Расчетные примеры
ПРИМЕР 1. Определить схему двухполюсника и определить параметры его элементов, если известны мгновенные ток и напряжение:
![]() ,
А
,
А
![]() ,
В.
,
В.
Решение:
Вначале определим сдвиг по фазе между напряжением и током
![]() ,
рад.
,
рад.
Поскольку сдвиг по фазе меньше нуля, то напряжение отстает от тока, что соответствует схеме R – C (рис. 4.1,в).
Параметры элементов рассчитываются по формулам (4.5) и (4.6):
![]() кОм;
кОм;
![]() кОм.
кОм.
Отсюда
![]() мкФ.
мкФ.
Таким образом, двухполюсник представляет собой последовательное соединение резистивного элемента сопротивлением 15,13 кОм и емкостного элемента с емкостью 0,08055 мкФ.
ПРИМЕР 2. Обратная задача. Двухполюсник состоит из последовательного соединения резистивного элемента сопротивлением 42 Ом и индуктивного элемента индуктивностью 0,1 Гн. К двухполюснику приложено синусоидальное напряжение 220 В частотой 50 Гц. Требуется определить ток и записать формулы мгновенного напряжения и тока.
Решение:
Считаем синусоидальное напряжение с нулевой начальной фазой, т.к. в условии задачи начальная фаза не задана и записываем мгновенное напряжение в виде:
![]() ,
В.
,
В.
Сдвиг по фазе между напряжением и током можно найти из формулы:
![]()
Отсюда
![]() рад.
рад.
Величину тока (в амперах) можно найти по закону Ома
![]()
Теперь мгновенный ток принимает вид:
![]() ,
А.
,
А.
Задача решена.
Задания для самостоятельной проработки
1. Изобразите графики (можно качественно, то есть приближенно) синусоидального напряжения и тока:
![]() ,
В;
,
В;
![]() ,
мА.
,
мА.
2. Запишите синусоидальную функцию тока, если начальная фаза задана не в радианах, а в градусах?
3. Рассчитайте полное сопротивление двухполюсника, если известны:
R = 1,1 кОм; С = 0,01 мкФ и период синусоидального тока 100 мкс.
4. Определите активное сопротивление двухполюсника, если его полное сопротивление 400 Ом, индуктивность индуктивного элемента равна 1 мГн, а частота синусоидального напряжения 50 кГц.
5. Рассчитайте сдвиг по фазе между напряжением и током пассивного двухполюсника, если его полное сопротивление 400 Ом, а активное сопротивление составляет 250 Ом. Действующие ток и напряжение соответственно равны 12 мА и 4,8 В.
Теоретические сведения "Параллельное соединение элементов"
Пассивным двухполюсником считают также часть цепи с параллельным соединением R–L и R–C- элементов (рис. 4.3).



Рис. 4.3 Схемы пассивных двухполюсников
при параллельном соединении
элементов:
а) общий случай; б)
R-С-цепь;
в) R-L-цепь
При таком представлении двухполюсников вместо сопротивлений вводят понятия проводимости: полную проводимость Y, активную G и реактивную B проводимости. Они рассчитываются по формулам:
![]() (4.7)
(4.7)
![]() (4.8)
(4.8)
![]() (4.9)
(4.9)
Следует обратить внимание на знак минус в последнем соотношении.
Очевидно равенство
![]() .
(4.10)
.
(4.10)
Аналогично двухполюсникам с последовательным соединением элементов здесь схема рис. 4.3,б соответствует отставанию напряжения по фазе от тока, а в схеме рис. 4.3,в – опережению напряжения по фазе тока.
Расчетные примеры
ПРИМЕР 3. Рассчитать активную и реактивную проводимости пассивного двухполюсника с параллельным соединением элементов, если задано:
U = 12 В, I = 0,24 A, R = 70 Ом.
Решение:
Активная проводимость определяется сразу
![]() ,
См;
,
См;
полная проводимость тоже может быть определена по току и напряжению
![]() ,
См;
,
См;
а реактивная проводимость рассчитывается из формулы (4.10):
![]() ,
См.
,
См.
ПРИМЕР 4. Заданы: мгновенное напряжение, емкость, и активное сопротивление пассивного двухполюсника с параллельным соединением элементов. Требуется определить мгновенный ток.
Дано:
![]() ,
В;
С
= 1 мкФ;
R
= 300 Ом.
,
В;
С
= 1 мкФ;
R
= 300 Ом.
Найти: i(t).
Решение:
Ток и напряжение связаны законом Ома, поэтому для определения тока нужно найти полную проводимость двухполюсника
![]() мСм.
мСм.
Тогда амплитуда тока равна Im = YUm = 4,25810–33,14 = 0,0134 А.
Поскольку
![]() ,
то
,
то
![]() рад.
рад.
Мгновенный ток теперь записывается в виде:
![]() А.
А.
Задания для самостоятельной проработки
1. Определите параметры элементов пассивного двухполюсника с параллельным соединением элементов, если заданы ток и напряжение
![]() ,
В;
,
В;
![]() ,
мА.
,
мА.
2. Определите схему пассивного двухполюсника с параллельным соединением элементов, если G = 0,03 См, В = 0,04 См.
3. Рассчитайте частоту тока и напряжения, если для пассивного двухполюсника с параллельным соединением элементов известны:
Y = 4,528 мСм; L = 30 мГн; R = 250 Ом.
4. Рассчитайте токи в элементах двухполюсника с параллельным соединением элементов, имеющего активную проводимость 1 мСм и реактивную проводимость –0,6 мСм, если действующее напряжение равно 2,4 В. Определите ток двухполюсника.
5. Для пассивного двухполюсника с параллельным соединением элементов известна полная проводимость Y = 0,02 См, и фазовый сдвиг между напряжением и током j = 0,75 рад. Определите активную и реактивную проводимости двухполюсника.
Теоретические сведения "Векторные диаграммы"
Для наглядного представления фазовых соотношений синусоидальные напряжения и токи представляют вращающимися векторами. При этом длина вектора в определенном масштабе является действующим или амплитудным значением синусоиды, а угол между вектором и осью абсцисс – начальной фазой синусоиды. На рис. 4.4 приведены возможные варианты векторных диаграмм для двухполюсников (сдвиг по фазе не может превышать по модулю угол /2 рад).

Длины векторов напряжения и тока связаны с масштабами напряжения mU и тока mI соотношением:
![]()
Отсюда следует,
что если выбрать
![]() ,
то длины векторов напряжения и тока
будут одинаковыми, что удобно при
изображении векторной диаграммы.
,
то длины векторов напряжения и тока
будут одинаковыми, что удобно при
изображении векторной диаграммы.
На векторных диаграммах можно изобразить векторы синусоидальных напряжений и токов отдельных элементов, входящих в схемы пассивных двухполюсников (рис. 4.1 и рис. 4.3). Для этого следует воспользоваться законом Ома для каждого элемента схемы двухполюсника.
В схемах рис. 4.1 напряжение и ток связаны соотношениями:
![]() ,
,
![]() ,
,
![]() .
.
При этом
для R-C-цепи:
![]() ,
для
R-L-цепи:
,
для
R-L-цепи:
![]() .
.
На рис. 4.5 приведены векторные диаграммы тока и напряжений элементов в схемах двухполюсников по рис. 4.1.
Из диаграмм хорошо
видно, что
![]() ,
является выражением закона Кирхгофа
для напряжений. При этом сумма напряжений
является не алгебраической, а геометрической
(векторной), поэтому длины векторов или
действующие напряжения элементов
связаны теоремой Пифагора (для
прямоугольного треугольника напряжений
с катетами UR
и UX
и гипотенузой U)
,
является выражением закона Кирхгофа
для напряжений. При этом сумма напряжений
является не алгебраической, а геометрической
(векторной), поэтому длины векторов или
действующие напряжения элементов
связаны теоремой Пифагора (для
прямоугольного треугольника напряжений
с катетами UR
и UX
и гипотенузой U)
![]() .
.

П оскольку
напряжения пропорциональны току,
выражение для полного сопротивления
оскольку
напряжения пропорциональны току,
выражение для полного сопротивления
![]()
также выражает теорему Пифагора (для прямоугольного треугольника сопротивлений с катетами R и X и гипотенузой Z), что показано на рис. 4.6.
Аналогично рис. 4.1 в схемах рис. 4.3 напряжение и ток связаны соотношениями:
![]() ,
,
![]() ,
,
![]() .
.
При
этом для R-C-цепи
![]() ,
а
для R-L-цепи
,
а
для R-L-цепи
![]() .
.
На рис. 4.7 приведены векторные диаграммы напряжения и токов элементов пассивного двухполюсника рис. 4.3.

Рис. 4.7. Векторные диаграммы тока и
напряжения пассивных двухполюсников:
а)
R-С-цепь
(напряжение отстает от тока); б)
R-L-цепь
(напряжение опережает ток); в)
R-цепь
(напряжение совпадает по фазе с током)
Из диаграмм следует,
что
![]() ,
является выражением закона Кирхгофа
для токов. При этом сумма токов является
не алгебраической, а геометрической
(векторной), поэтому длины векторов или
действующие токи элементов связаны
теоремой Пифагора (для прямоугольного
треугольника токов с катетами IG
и IB
и гипотенузой I)
,
является выражением закона Кирхгофа
для токов. При этом сумма токов является
не алгебраической, а геометрической
(векторной), поэтому длины векторов или
действующие токи элементов связаны
теоремой Пифагора (для прямоугольного
треугольника токов с катетами IG
и IB
и гипотенузой I)
![]() .
.
П оскольку
токи пропорциональны напряжению,
выражение для полной проводимости
оскольку
токи пропорциональны напряжению,
выражение для полной проводимости
![]() также
выражает теорему Пифагора (для
прямоугольного треугольника проводимостей
с катетами G
и B
и гипотенузой Y).
Поэтому на рис. 4.8 приведены треугольники
проводимостей пассивных двухполюсников.
также
выражает теорему Пифагора (для
прямоугольного треугольника проводимостей
с катетами G
и B
и гипотенузой Y).
Поэтому на рис. 4.8 приведены треугольники
проводимостей пассивных двухполюсников.
Рис. 4.8. Треугольники проводимостей
пассивных двухполюсников:
а)
R-С-цепь
(напряжение отстает от тока); б)
R-L-цепь
(напряжение опережает ток)
ПРИМЕР 5. Определить параметры пассивного двухполюсника неразветвленной цепи с последовательным соединением индуктивной катушки (имеющей неизвестное активное сопротивление rK и неизвестную индуктивность LK) и резистора с известным сопротивлением R, если измерены напряжения на резисторе UR, индуктивной катушке UK и на зажимах двухполюсника U. Схема двухполюсника приведена на рис. 4.9,а.
Uк
I





Lк
R
UR
rк
Urк
ULк







U


а)
б)
в)
г)
Рис. 4.9. Схема а), векторная
диаграмма б), треугольник
напряжений в) и треугольник
сопротивлений г) пассивного
двухполюсника
На рис. 4.9,б
приведена векторная диаграмма напряжений
и тока цепи. С помощью этой диаграммы
можно построить треугольники напряжений
рис. 4.9, в
и треугольники сопротивлений рис.4.9,г.
Сдвиг по фазе
между напряжением и током определяется
из треугольника напряжений рис.4.9,в
по теореме косинусов:
![]() .
Общий ток всех элементов можно рассчитать
по закону Ома для резистивного элемента
.
Общий ток всех элементов можно рассчитать
по закону Ома для резистивного элемента
![]() ,
затем легко рассчитать сопротивления
(параметры двухполюсника) из треугольников
сопротивлений:
,
затем легко рассчитать сопротивления
(параметры двухполюсника) из треугольников
сопротивлений:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Исследование модели разветвленной цепи в пакете EWB /Самостоятельная работа
В пакете Electronics
Workbench
(EWB)
собрать схему цепи (рис. 4.10), приняв
параметры источника (U0
и f)
и резисторов (R2
и R3)
согласно варианту задания (табл. 4.1.). На
рис. 4.11,а
приведена полученная схема для одного
из вариантов.
пакете Electronics
Workbench
(EWB)
собрать схему цепи (рис. 4.10), приняв
параметры источника (U0
и f)
и резисторов (R2
и R3)
согласно варианту задания (табл. 4.1.). На
рис. 4.11,а
приведена полученная схема для одного
из вариантов.
Рис. 4.10
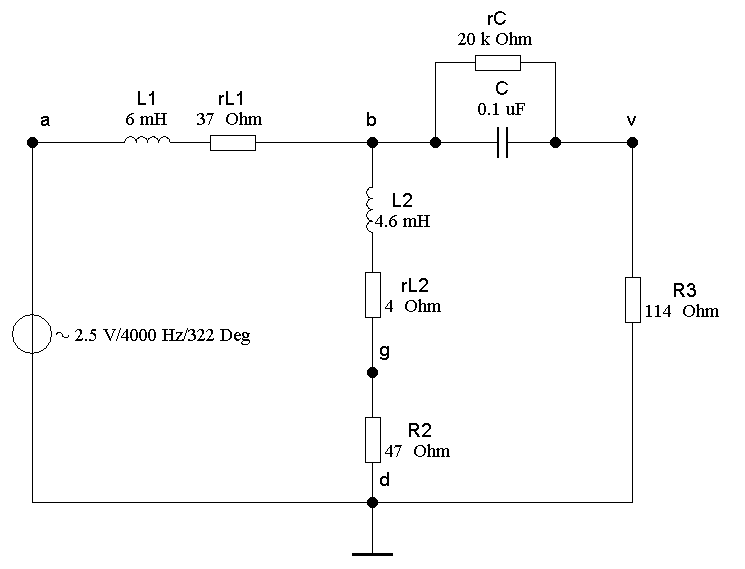
1. Двухполюсники (rL1 – L1), (rL2 – L2) и (rC – C) сделать подсхемами цепи. Для этого: 1) установить курсор мыши левее и выше элемента rL1 нажать и не отпускать левую кнопку и протащить курсор вниз вправо (показано на рис. 4.11,а в виде прямоугольника и стрелки), чтобы возникший прямоугольник пересек горизонтальные линии, а внутрь прямоугольника попали элементы rL1 и L1 , затем отпустить кнопку. В результате оба элемента будут выделены красным цветом. 2) В меню «Circuit» выбрать команду «Create Subcircuit…», с клавиатуры ввести имя RL1, затем мышью нажать на кнопке «Replace in Circuit». В результате откроется окно подсхемы, в котором будут показаны входящие в нее элементы и внешние зажимы (контакты) – рис. 4.11, б.
Закрыть окно подсхемы и проделать то же для двухполюсника (rL2 – L2), назвав подсхему "RL2". Аналогично создать подсхему с именем "CR1" (на рис. 4.11, а пунктиром показаны области выделения для создания этой подсхем). В результате получится цепь рис. 4.12.
a



 )
)
б)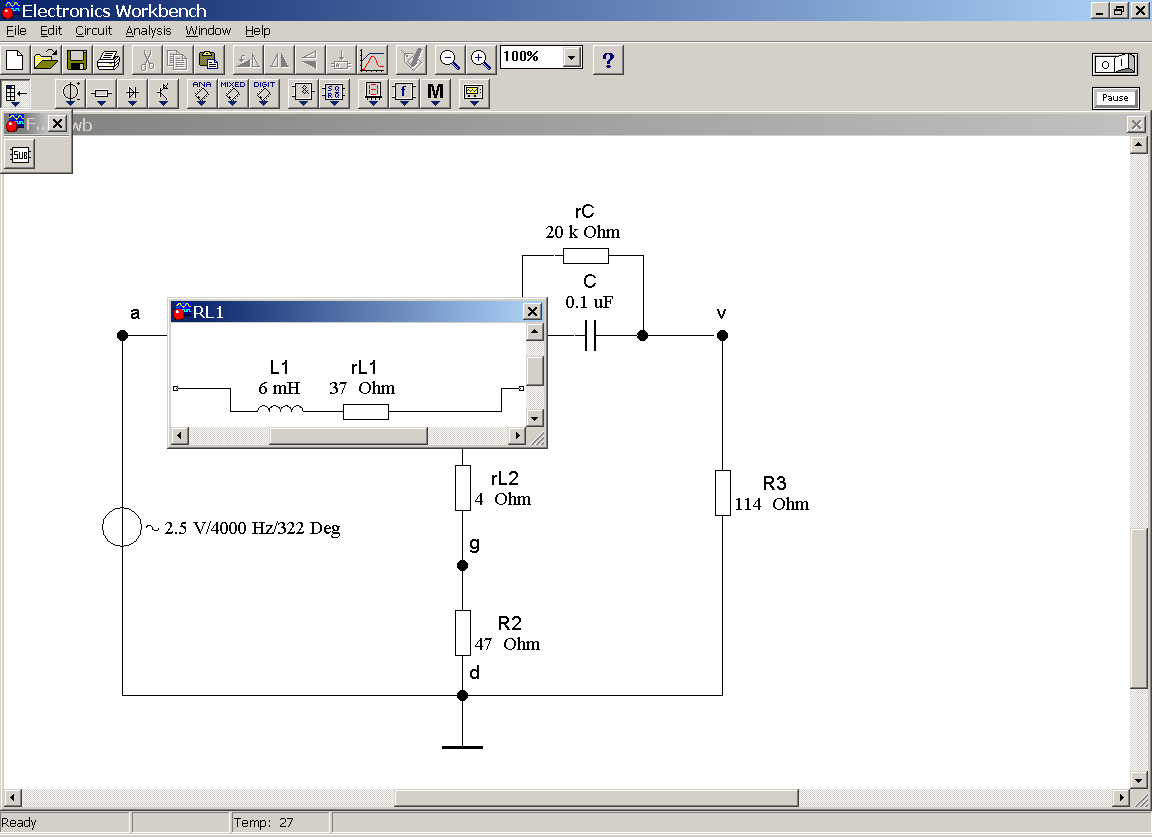
Рис. 4.11
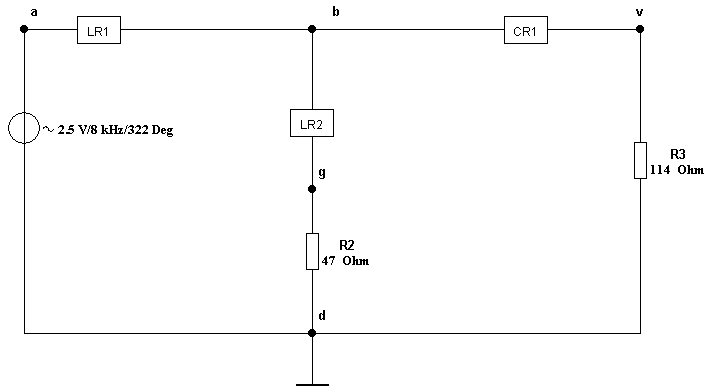
Рис. 4.12
-
Таблица 4.1
Таблица 4.1 (Продолжение)
Вариант
U0,
В
f,
Гц
R2,
Ом
R3,
Ом
Вариант
U0,
В
f,
Гц
R2,
Ом
R3,
Ом
1
3
3500
40
120
16
2
4500
68
82
2
3
3500
42
116
17
2
4500
66
86
3
3
3500
44
112
18
2
4500
64
90
4
3
3500
46
108
19
2
4500
62
94
5
3
3500
48
104
20
2
4500
60
98
6
2
3000
50
100
21
3
5000
58
102
7
2
3000
52
96
22
3
5000
56
106
8
2
3000
54
92
23
3
5000
54
110
9
2
3000
56
88
24
3
5000
52
114
10
2
3000
58
82
25
3
5000
50
118
11
2.5
4000
60
120
26
4
3500
48
122
12
2.5
4000
62
116
27
4
3500
46
120
13
2.5
4000
64
112
28
4
3500
44
116
14
2.5
4000
66
108
29
4
3500
42
112
15
2.5
4000
68
104
30
4
3500
40
108
2. Подключить амперметры и вольтметры для измерения всех токов и напряжений рис. 4.13.
3. Снять показания приборов для двух значений частот: f1 = f и f2 = 2f и записать данные в табл. 4.2.
4. Рассчитать фазовые сдвиги между напряжениями и токами двухполюсников RL2 и RC1. Для этого построить векторные диаграммы тока и напряжений для каждого двухполюсника (подсхемы), а также векторные суммы напряжений по второму закону Кирхгофа.
5. Рассчитать комплексные значения всех измеренных токов и напряжений (для RL2 и RC1), приняв начальную фазу тока в R3 за нуль.
6. Рассчитать активные и реактивные сопротивления двухполюсников.
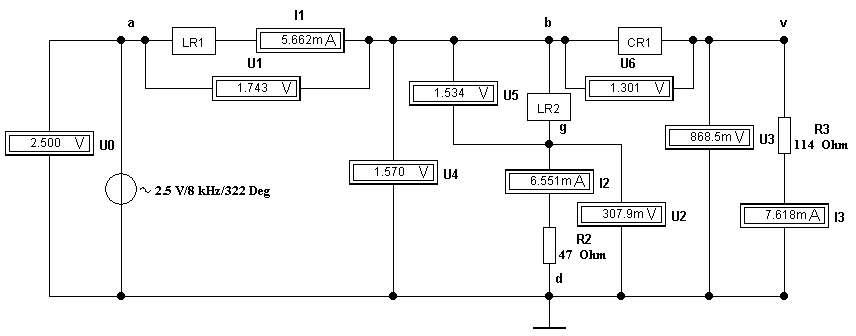
Рис. 4.13
Таблица 4.2
f, кГц |
I1, мА |
I2, мА |
I3, мА |
U0 (Uad), В |
U1 (Uab), В |
U2 (Ugd), В |
U3 (Uvd), В |
U4 (Ubd), В |
U5 (Ubg), В |
U6 (Ubv), В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчеты и построения
Для построения диаграмм и треугольников сопротивлений следует воспользоваться «методом трех вольтметров», заключающимся в том, что строится треугольник векторов напряжений элементов ветви и всей ветви. Он получается из векторного уравнения закона Кирхгофа для напряжений. Из этого треугольника определяется угол между вектором напряжения ветви и вектором напряжения на R – элементе (тока).
Построения и расчеты рассмотрим на примере: предположим, что измерены следующие токи и напряжения:
f, кГц |
I1, мА |
I2, мА |
I3, мА |
U0 (Uad), В |
U1 (Uab), В |
U2 (Ugd), В |
U3 (Uvd), В |
U4 (Ubd), В |
U5 (Ubg), В |
U6 (Ubv), В |
8000 |
5,12 |
6,81 |
7,16 |
2,50 |
1,58 |
0,320 |
0,816 |
1,63 |
1,60 |
1,41 |
Сопротивления элементов равны: R2 = 47 Ом и R3 = 114 Ом.
Построим
векторные диаграммы
для двухполюсников RL2
и RC1.
По закону Кирхгофа для напряжений можно
записать (векторно):
![]() и
и
![]() .
Напряжения, входящие в уравнения,
образуют треугольники, которые можно
построить по трем сторонам, как
показано на рисунке.
.
Напряжения, входящие в уравнения,
образуют треугольники, которые можно
построить по трем сторонам, как
показано на рисунке.
R
= kUU5
R
= kUU2
d
b
g







R
= kUU6
R
= kUU3
d
b
v





Здесь R – радиус дуг, пропорциональный соответствующим напряжениям.
Коэффициент пропорциональности kU является масштабом по напряжению (В/мм).
Эти треугольники позволяют построить векторы напряжений на сторонах. Вершины являются местами подключения элементов. Направления векторов должно быть ПРОТИВОПОЛОЖНО направлению напряжений на схеме цепи. Так, если на участке bd схемы цепи напряжение направлено от точки b к точке d, то в треугольнике напряжений – наоборот!
U2
U4
U5
d
b
g
d
b
v
U3
U4
U6





Направления тока и напряжения на резистивных элементах одинаково, поэтому вектор тока I2 направлен по вектору U2, а вектор I3 направлен по вектору U3. Следует подчеркнуть, что вектор U2 отстает от вектора U4 (двухполюсник RL), а вектор U3 опережает вектор U4 (двухполюсник RC).


g
2
3
I2
U2
U4
U5
d
b
d
b
v
U3
U4
U6
I3
Сдвиг по фазе между напряжением и током ветви может быть найден по теореме косинусов из треугольников:
 рад;
рад;
 рад.
рад.
П оскольку
вектор напряжения U4
общий для двух ветвей, то две векторные
диаграммы и треугольники напряжений
можно объединить в одну диаграмму, как
это показано на рисунке слева.
оскольку
вектор напряжения U4
общий для двух ветвей, то две векторные
диаграммы и треугольники напряжений
можно объединить в одну диаграмму, как
это показано на рисунке слева.
Из этой диаграммы следует, что фазовый сдвиг между векторами токов I2 и I3 равен 2 + 3. Зная векторы токов I2 и I3 можно рассчитать ток I1 по закону Кирхгофа для токов в узле b:
I1 = I2 + I3.
Длина вектора тока I1 определяется из треугольника, образованного векторами токов, по теореме косинусов:
![]()
![]() .
.
Отсюда
![]() мА.
мА.
Сдвиг по фазе между токами I1 и I3 равен 3 – 1.
Этот угол также можно найти из треугольника токов по теореме косинусов:


Для напряжений U0, U1 и U4 также можно построить треугольник и определить сдвиг по фазе 4 между напряжениями U1 и U4 (рисунок слева):
 рад.
рад.
Д ля
расчета комплексных токов,
напряжений и сопротивлений можно
воспользоваться полученными данными.
По условию задания следует принять
нулевой начальную фазу вектора тока
I3.
Это равносильно повороту ВСЕХ диаграмм
по часовой стрелке на угол 3.
В результате получится векторная
диаграмма напряжений и токов на
комплексной плоскости, где вектор
I3
направлен по вещественной оси (рис.
4.14). Начальные фазы токов I1
и I2
соответственно будут равны i1
= (3
– 1),
i2 =
– (2
+ 3).
ля
расчета комплексных токов,
напряжений и сопротивлений можно
воспользоваться полученными данными.
По условию задания следует принять
нулевой начальную фазу вектора тока
I3.
Это равносильно повороту ВСЕХ диаграмм
по часовой стрелке на угол 3.
В результате получится векторная
диаграмма напряжений и токов на
комплексной плоскости, где вектор
I3
направлен по вещественной оси (рис.
4.14). Начальные фазы токов I1
и I2
соответственно будут равны i1
= (3
– 1),
i2 =
– (2
+ 3).
Комплексные токи будут равны:
![]() ,
,
![]() и
и
![]() .
.
Комплексные напряжения оказываются равны:
![]() ,
,
![]() ,
,
![]() ,
где
,
где
 .
.
Зная комплексные напряжения и комплексные токи, можно рассчитать комплексные сопротивления двухполюсников:
![]() ,
,
![]() ,
,
![]() .
.
