Проведение расчетов

Для расчетов используется математический пакет MathCad PLUS 5.

Ниже приводится лист MathCad с выполненными расчетами и комментариями.

Целесообразно исходные данные задавать в виде компонентов векторов, а расчеты проводить в матричной форме

- этот оператор устанавливает номер первого элемента вектора (по умолчанию он равен нулю)

Для ввода векторов необходимо после оператора присвоения ":=" вызвать диалоговое окно "Matrices" путем комбинации клавиш Ctrl+M,

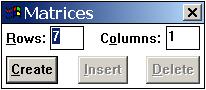
Затем в полях ввода установить 7 строк и 1 столбец и мышкой "нажать" кнопку "Create" (создать). После этого появляется шаблон с незаполненными элементами вектора. Для заполнения матрицы доста­точно вводить нужные числа и для перехода к следующему элементу нажимать клавишу табуляции или щелкать мышкой.

Теперь можно задать матрицу коэффициентов при неизвестных системы кон­турных уравнений (2.2) и вектор правых частей

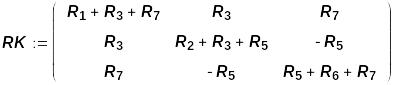
Индексы вводятся после нажатия открывающей квадратной скобки [

Для ввода слагаемых с индексом нужно после ввода индекса нажать на клавишу "Пробел", а затем на "+"

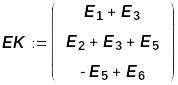
Далее вводится выражение решения системы уравнений

Ввод осуществляется в такой последовательности:

I K Shift+; R K Shift+6 – 1 "Пробел" * E K "Enter"

Для вывода на экран решения нужно просто написать IK =

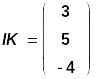
Верхнее число соответствует первому току, среднее – второму, нижнее – третьему. Зная контурные токи, можно определить токи в ветвях, для этого можно в матричной форме ввести соотношения (2.1):

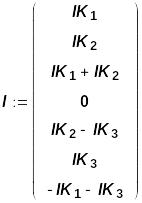
Для вывода на экран токов ветвей нужно просто написать I =

_.

Здесь верхнее число равно первому току, а нижнее – седьмому. Напряжения R - элементов определяются по закону Ома

- счетчик с шагом 1.

Вводится так: k Shift+; 1 ; 7 Enter

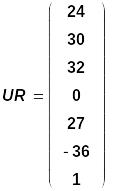
Напряжения ветвей определяются по компонентным уравнениям

Правильность расчетов можно проверить, составив баланс мощностей:

Мощность всех приемников цепи равна:

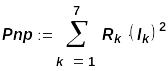
Для ввода оператора суммы необходимо на панели инструментов (слева у обреза экрана) нажать мышкой соответствующую кнопку.

Мощность всех источников цепи равна:

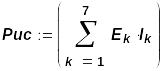
Итак, баланс мощностей выполнен и, значит, все расчеты верны.

МЕТОД УЗЛОВЫХ НАПРЯЖЕНИЙ

Суть метода узловых напряжений состоит в следующем: напряжения ветвей выражаются через узловые потенциалы, то есть через напряжения узлов относительно одного узла, называемого "опорным", токи ветвей выражаются через узловые потенциалы и подставляются в уравнения Кирхгофа для токов в узлах, полученные уравнения решаются относительно узловых потенциалов.

Поскольку "узловых" напряжений обычно зна­чительно меньше, чем напряжений ветвей, то метод позволяет существенно снизить трудоемкость расчетов.

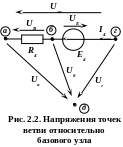
На рис. 2.2 показана ветвь электрической цепи с обозначенными: током I и напряжениями элеме­нтов U_R , U_E и всей ветви U_га. Точка д принята в качестве опорного узла, относительно которого отсчитываются напряжения. Напряжения элементов и всей ветви, выраженные через потенциалы, равны:

, и .

Напряжения элементов U_R , U_E и всей ветви U_га можно выразить через напряжения узлов (точек) U_а , U_б , U_г относительно некоторой (произвольно выбранной) точки "д" так:

,

,

.

Из этих выражений следует, что вместо потенциалов узлов (точек) мо­ж­но записывать напряжения этих точек относительно любой другой точки! Поэтому в электрических цепях вместо понятия "потенциал" используется понятие "напряжение" (разность потенциалов).

С учетом полученных соотношений уравнение для напряжения ветви мо­ж­но записать через узловые напряжения в виде:

(2.3)

или

. (2.4)

Эти уравнения показывают, что ток ветви выражается через напряжения узлов U_г и U_а, к которым подключена данная ветвь, проводимость резис­ти­в­ного элемента G и напряжение источника E. В этом уравнении напряжения в скобках записаны в такой последовательности: вначале напряжение (U_г) узла от которого направлен ток ветви, а затем напряжение (U_а) узла, к которому направлен ток ветви.

Д ля рассчитываемой цепи в качестве опорного принимаем четвертый узел, то есть узел "г", тогда уравнения напряжений ветвей по (2.3) можно записать в виде:

,

,

(2.5)

,

,

.

,

здесь узел "а" обозначен "1", узел "б" – "2" и узел "в" – "3".

Подставив эти выражения в уравнения закона Кирхгофа для токов в первых трех узлах и приведя подобные члены, получим:

для узла "а" – "1": ,

или ; (2.6,а)

для узла "б" – "2": ,

или ; (2.6,б)

для узла "в" – "3": ,

или . (2.6,в)

Уравнения (2.6) называются "узловые уравнения". Их решение позволит рассчитать токи ветвей по (2.5), то есть решить задачу анализа цепи.