
R1
= 8 Ом; R2
= 6 Ом; R3
= 4 Ом;
R4
= 8 Ом; R5
= 3 Ом; R6
= 9 Ом;
R7
= 1 Ом;
Е1
= 45 В;
Е2 =
9 В;
Е3 =
10 В;
Е4
= 100;
Е5 =
70 В;
Е6 =
6 В.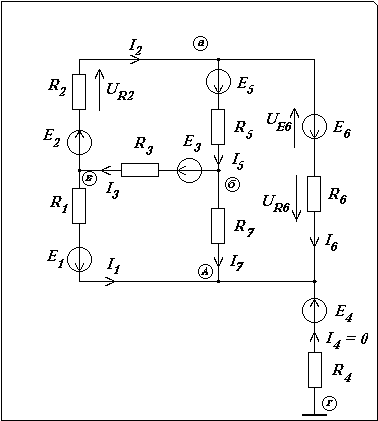
Параметры элементов:

Предварительный анализ цепи:
Поскольку узел «г» – земля, не соединен ни с какими другими узлами, то тока в четвертой ветви нет, то есть I4 = 0. Тогда при расчетах эту ветвь можно из схемы исключить.
На аудиторном практическом занятии эта цепь была рассчитана с помощью уравнений по законам Кирхгофа и Ома. Теперь самостоятельно необходимо рассчитать цепь другими методами. Рассмотрим методы контурных токов и узловых напряжений.
Метод контурных токов
Метод контурных токов применяют для расчета токов всех ветвей в цепях, для которых число независимых контуров "к" не больше числа независимых узлов "у-1", то есть когда выполняется условие:
в – у + 1 – вJ у – 1,
где в – число ветвей (с токами), вJ – число источников тока, у – число узлов.
Для рассчитываемой цепи это условие имеет вид: 6 – 4 + 1 – 0 4 – 1.
Суть метода состоит в предположении, что в каждом независимом контуре цепи по всем его элементам протекает некоторый “контурный ток”. В результате по некоторым элементам, принадлежащим одновременно нескольким контурам, протекают несколько контурных токов, алгебраическая сумма которых и определяет фактический ток в элементе. Если элемент входит только в один контур, то его ток равен контурному. Направления токов определяются в соответствии с условными положительными направлениями и знаками численных значений контурных токов. Уравнения по закону Кирхгофа для напряжений в контуре, записанные через контурные токи, называются системой контурных уравнений и позволяют рассчитать контурные токи.
Выбор контуров. Независимая система контуров выбирается с помощью ориентированного графа схемы цепи. Этот граф представляет собой «скелет» схемы цепи. Каждая ветвь изображается линией (независимо от набора элементов ветви), а узел – точкой. Для заданной схемы граф показан на рис. 2.1, а.

Рис. 2.1
Вначале необходимо выбрать «дерево графа», то есть ветви, соединяющие все узлы, но не образующие контуров. Можно получить несколько различных деревьев. Однако при выборе дерева следует руководствоваться следующим правилом: в первую очередь включаются ветви, состоящие только из источников напряжения, потом ветви с последовательным соединением R– и Е– элементов, в последнюю очередь ветви с R– элементами. Поскольку в заданной цепи отсутствуют ветви, состоящие только из источника напряжения, то выберем дерево из ветвей R–E: 3-й, 5-й и 7-й (рис. 2.1,б).
Независимые контуры образуются путем добавления к ветвям дерева по одной из оставшихся ветвей графа. Эти ветви называются ветвями связи. На рис. 2.1 в–д приведены образованные так контуры.
Формирование контурных уравнений. Контурные уравнения записывают по закону Кирхгофа для напряжений в контурах цепи, определяя вначале токи элементов через контурные токи. На рис. 2.1 внутри контуров показаны и обозначены через IК контурные токи. Направления этих токов определяются токами ветвей связи.
Ток элемента представляют собой алгебраическую сумму контурных токов в данном элементе. Поэтому для тока в элементах первой ветви эта сумма состоит из одного слагаемого:
I1 = IK1
Для тока в элементах второй ветви, аналогично:
I2 = IK2
А вот для тока в третьей ветви число слагаемых равно двум, поскольку ветвь 3 входит в первый и второй контуры:
I3 = IK1 + IK2
В этой формуле все слагаемые со знаком «+» поскольку ток ветви и контурные токи в этой ветви направлены одинаково.
Ток пятой ветви также определяется двумя контурными токами, поскольку эта ветвь входит во второй и третий:
I5 = IK2 – IK3
Здесь третий контурный ток со знаком «–», поскольку в ветви 5 этот ток направлен встречно принятому направлению тока ветви. Аналогично получим:
I6 = IK3
I7 = – IK1 –IK3
С учетом двух последних соотношений токи ветвей оказываются равны:
I 1
= IK1
1
= IK1
I2 = IK2
(2.1)
I5 = IK2 – IK3
I6 = IK3
I7 = – IK1 –IK3
Теперь можно записать контурные уравнения по закону Кирхгофа для напряжений. Для второго контура: U2 + U3 + U5 = 0, а с учетом компонентных уравнений:
R2I2 – E2 + R3I3 – E3 + R5I5 – E5 = 0
Для первого контура:
R1I1 – E1 + R3I3 – E3 – R7I7 + E7 = 0
Для третьего:
– R5I5
– E5
+ R6I6
– E6
– R7I7
+ E7
= 0
R5I5
– E5
+ R6I6
– E6
– R7I7
+ E7
= 0
Подставив в эти уравнения выражения для токов ветвей через контурные, и, приводя подобные члены, получим:
(
(2.2)
R3IK1 + (R2 + R3 + R5)IK2 – R5IK3 = E2 + E3 + E5;
R7IK1 – R5IK2 + (R5 + R6 + R7)IK3 = –E5 + E6.
Это и есть система контурных уравнений. В уравнениях учтено, что Е7 = 0 (см. схему цепи).
После решения системы контурных уравнений рассчитываются токи ветвей. Зная токи ветвей, можно определить напряжения всех R–элементов по закону Ома.
Правильность расчетов проверяется с помощью баланса мощностей:
Рпр = Рис
![]() и
и
![]()
