Практические занятия

По дисциплине предусмотрены аудиторные и домашние практические занятия, которые предназначены для расчета типовых задач и освоения основных методов расчета (анализа) электрических цепей.

В пособие включены отдельные практические занятия, которые вынесены либо на самостоятельную проработку, либо представляют определенные трудности для студентов на аудиторных занятиях. Кроме того отдельные занятия можно рассматривать как подготовку к выполнению домашних расчетных заданий.

Расчет цепей постоянного тока с одним источником

Расчеты проводят для правильного выбора проводников (материал, поперечное сечение) и режимов работы элементов цепи. При этом рассчитываются токи, напряжения и мощности.

В качестве примера рассмотрим часть бортовой сети автомобиля, сос­то­я­­щей из источника напряжения (аккумулятора или генератора постоянного напряжения), проводников и потребителей (ламп накаливания).

Для расчета цепи все элементы представляются упрощенными физическими моделями, отражающими их назначение:

• источник напряжения превращает неэлектрическую энергию в энергию постоянного тока (Е  12 В);

• проводники служат для соединения источника с приемниками и представляют собой резистивные элементы, превращающие энергию электрического тока в тепло;

• приемники – лампы накаливания также представляются резистивными элементами.

Рис. 1.1 Принципиальная схема цепи

На схеме обозначены: Е – ЭДС (напряжение источника); r – резистивный элемент, превращающий часть энергии источника в тепло (учитывает неидеальность аккумулятора, или генератора, как источника напряжения); R_пр1 и R_пр2 – резистивные элементы, имеющие сопротивления соединительных проводов; R_л1, R_л2, R_л3, R_л4 и R_л5 – резистивные элементы, имеющие сопротивления соответствующих лампочек. Обычно «минус» аккумулятора соединен с массой кузова, поэтому любая металлическая часть кузова имеет более низкий потенциал, чем любая точка бортовой электрической сети (цепи), не соединенная с корпусом. Очевидно, что благодаря значительной площади поперечного сечения, кузов имеет очень малое сопротивление, которое можно считать нулевым по сравнению с другими сопротивлениями. Значит все точки в цепи, соединенные с кузовом, можно замкнуть проводником с нулевым сопротивлением (на рис. 1.1 показан пунктиром).

Для удобства расчетов все элементы нумеруются, а не обозначаются буквенными индексами. Соединительные линии (идеальные проводники) на схемах обычно показываются горизонтальными и вертикальными прямыми. Клеммы элементов (показаны окружностями на рис. 1.1) обозначают точками на соединительных проводниках. В результате расчетная схема цепи принимает вид, представленный на рис. 1.2.

Рис. 1.2 Расчетная схема цепи

Обычно при проведении расчетов бывают заданы: схема цепи и параметры всех ее элементов. Поэтому считается, что известны: Е = 12.3 В; r = 0.011 Ом; R₁ = 0.025 Ом; R₄ = 0.032 Ом; R₂ = ? – не задано, но для этой лампочки известны номинальное напряжение 12 В и номинальная мощность 23 Вт, на которые она рассчитана; R₃ = ? – не задано, но известны: напряжение 12 В и мощность 2 Вт; R₅ = ? – не задано, но известны: напряжение 12 В и мощность 40 Вт; R₆ = R₂; R₇ = R₅.

Обычно требуется рассчитать токи всех элементов цепи и напряжения приемников (лампочек).

Расчет ведется по следующему алгоритму:

1 В расчетной схеме цепи выбираются направления и обозначаются токи и напряжения элементов.

При этом целесообразно пользоваться такими правилами:

• в ветвях с источниками напряжения направлять ток в направлении стрелки ЭДС,

• напряжения направлять в сторону убывания потенциала.

На рис. 1.3,а показано направление тока I₁ в ветви с источником в виде стрелки на соединительной линии.

Этот ток разветвляется в точке «а» на токи I₂, I₃ и I₄, поэтому эти токи на рис. 1.3,б показаны направленными от узла (точки) «а». Ток I₄ в точке «б» разветвляется на токи I₅, I₆ и I₇, поэтому эти токи показаны от узла «б».

Замечание: следует учесть, что в схеме рис. 1.3,а не семь узлов, а только три. Это связано с тем, что узлом считают МЕСТО СОЕДИНЕНИЯ ЭЛЕМЕНТОВ, а не место соединения линий схемы цепи. Поскольку между точками «а» и «а'» нет элементов, то эти точки являются одним и тем же узлом «а», аналогично точки «0» и «0'», «0''» и «0'''» являются одним узлом "0".

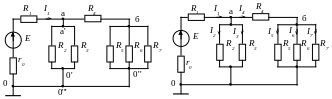
а) б)

Рис. 1.3 Выбор направлений и обозначение токов элементов

После выбора токов можно указать направления напряжений. Поскольку за направление тока принимают направление положительных зарядов, то ток направлен от точки с бо;´льшим потенциалом к точке с меньшим потенциалом (в сторону убывания). Значит, направление напряжения совпадает с направлением тока и указывается стрелкой рядом с элементом, как это показано на рис. 1.4. Для источника напряжения направление напряжения U_Е не совпадает с направлением ЭДС Е, поскольку стрелка ЭДС указывает на зажим (вывод, точку) с бо;´ль­шим потенциалом.

Рис. 1.4 Выбор направлений и обозначение напряжений элементов

Упрощается схема цепи путем замены последовательно и параллельно соединенных резистивных элементов эквивалентными. При этом в преобразованной схеме показываются токи и напряжения всех эквивалентных элементов.

2Упрощается схема цепи путем замены последовательно и параллельно соединенных резистивных элементов эквивалентными. При этом в преобразованной схеме показываются токи и напряжения всех эквивалентных элементов.

На схеме рис. 1.4: r₀ и R₁ соединены последовательно, R₂ и R₃ соединены параллельно, R₅, R₆ и R₇ соединены параллельно, заменяя их соответствующими эквивалентными элементами, получим цепь рис. 1.5,а. Здесь эквивалентные сопротивления равны:

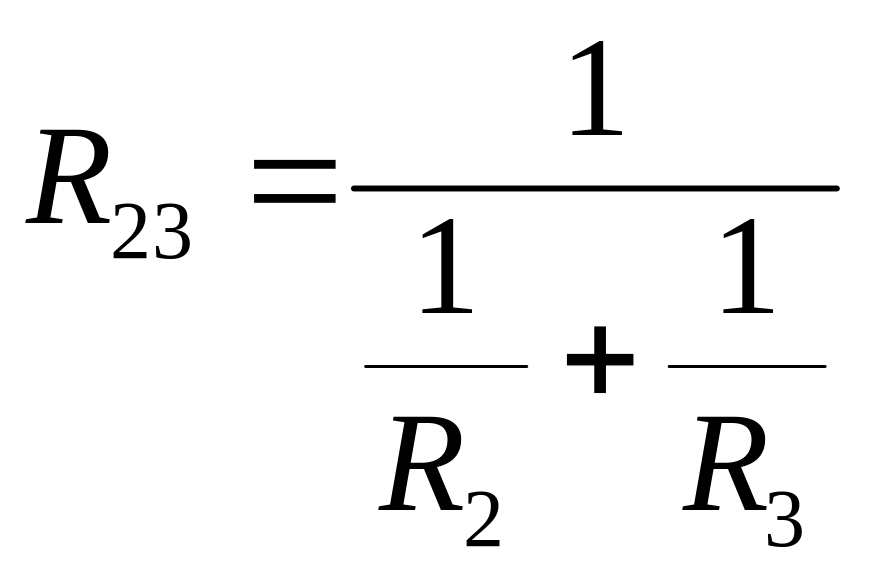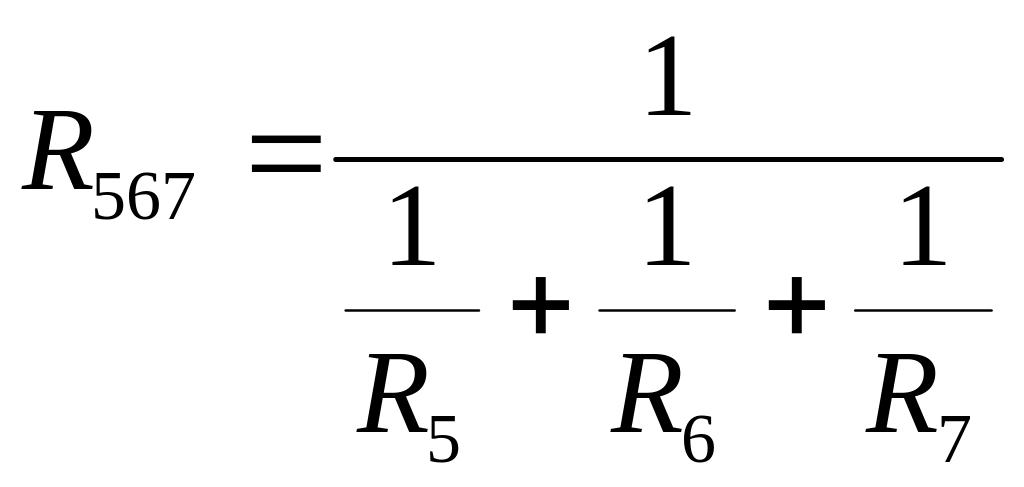; ; . (1.1)

Поскольку на элементах при параллельном соединении одинаковое нап­ряжение, то в преобразованной цепи на эквивалентных элементах R₂₃ и R₅₆₇ остается это же напряжение (U₂ и U₅).

а) б)

Рис. 1.5 Схема цепи после первых преобразований

3Повторяется п.2 до тех пор, пока в преобразованной цепи останется один источник и один резистивный элемент.

В схеме рис.1.5,а R₄ и R₅₆₇ оказываются соединены последовательно и по­этому могут быть заменены эквивалентным R₄₇, что и показано на рис. 1.5,б.

При этом

. (1.2)

В свою очередь в полученной схеме R₂₃ и R₄₇ соединены параллельно и также заменяются эквивалентным (рис. 1.6,а), при этом

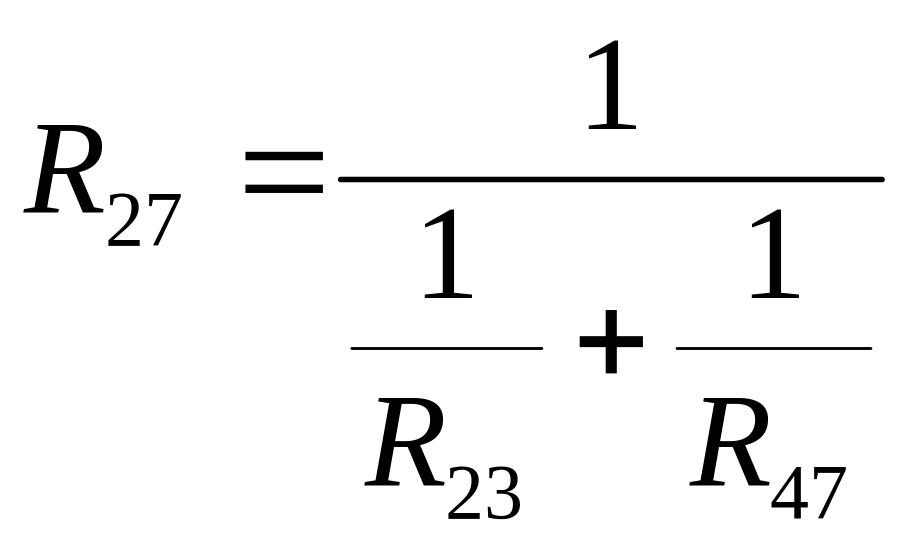. (1.3)

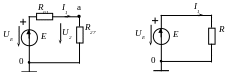
а) б)

Рис. 1.6 Схема после всех преобразований

Наконец, R₀₁ и R₂₇ на рис. 1.6,а соединены последовательно и могут быть заменены одним эквивалентным элементом R, сопротивление которого:

. (1.4)

В результате, получилась элементарная цепь (рис. 1.6,б), в которой два элемента соединены как последовательно, так и параллельно, то есть у них одинаковы как токи и напряжения.

4В полученной цепи по закону Ома определяется ток и с его помощью рассчитываются токи и напряжения в предыдущих преобразованных схемах, а затем и в исходной.

Ток резистивного элемента цепи рис. 1.6,б определяется по закону Ома:

. (1.5)

В последней схеме (рис. 1.6,б) оказываются известными все токи и все напряжения. Поэтому переходим к расчетам предыдущих схем.

В цепи рис. 1.6,а обозначенное напряжение U₂ (на эквивалентном резистивном элементе параллельного соединения R₂₃ и R₄₇) равно:

. (1.6)

Поскольку других неизвестных и обозначенных токов и напряжений в этой цепи нет, то переходим к расчету предыдущей схемы (рис. 1.5,б). Здесь неизвестными являются только токи. Они определяются по закону Ома по известному напряжению и сопротивлениям элементов:

; . (1.7)

Далее в цепи рис. 1.5,а определяется напряжение U₅ (на эквивалентном резис­ти­вном элементе параллельного соединения R₅, R₆ и R₇):

. (1.8)

Поскольку теперь в этой цепи известны все обозначенные токи и напряжения, то переходим к расчету по закону Ома токов и напряжений в исходной расчетной схеме рис. 1.4.

; ; (1.9)

; ; ; ; . (1.10)

Таким образом, определены все токи и напряжения элементов цепи и задача оказывается решенной.

5Для проверки правильности расчетов составляется баланс мощностей исходной расчет­ной схемы.

Поскольку в цепи один источник, то его мощность должна быть равна сумме мощностей всех резистивных элементов:

. (1.11)

Первое слагаемое обусловлено тем, что в элементе r₀ ток I₁, а не I₀.

Замечание: Приведенный алгоритм работает в любых цепях с одним источником, если нет мостового соединения элементов. Признаком такого соединения является соединение элементов в треугольники и в звезды. В этом случае для упрощения схе­мы цепи используется эквивалентное преобразование соединения элементов в треугольник в соединение элементов в звезду или наоборот.

Формулы эквивалентных преобразований звезды резистивных элементов с сопротивлениями R_а, R_б и R_в в треугольник элементов с сопротивлениями R_аб, R_бв и R_ва и наоборот имеют вид (обозначения соответствуют схемам на рис. 1.7,а и б):

Преобразование
Звезды в треугольник		Треугольника в звезду

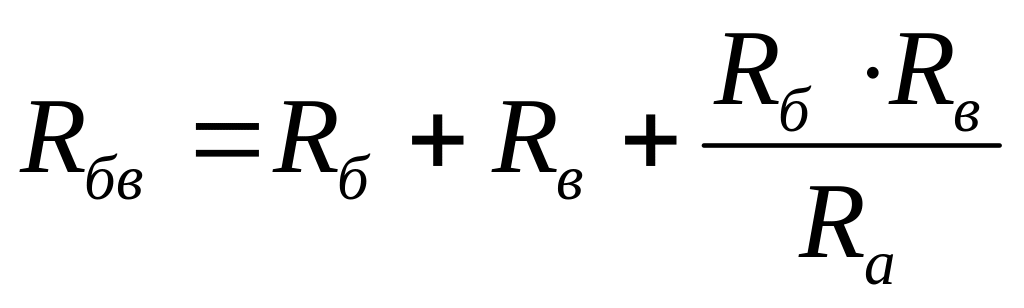
а) б)

Рис. 1.7 Эквивалентные преобразования соединения элементов из треугольника в звезду и наоборот