Порядок выполнения

Лабораторная работа состоит из двух частей:

- расчет траектории полета неуправляемого ЛА;

- оптимизация траектории полета неуправляемого ЛА.

Часть 1. Расчет траектории неуправляемого ла.

Расчет траектории неуправляемого ЛА выполняется в следующей последовательности:

1. Составить математическую модель движения центра масс ЛА при принятых допущениях.

2. Используя численный метод, составить программу решения уравнений на ЭВМ (с использованием программных приложений MicroSoft Excel или MathCad, или на любом языке программирования).

3. После отладки программы провести вычисление изменения параметров траектории от времени (исходные данные для расчета в приложении 1), и по ним определить следующие основные элементы траектории:

- максимальная высота траектории;

- параметры траектории в конце активного участка (скорость, дальность, высоту);

- скорость, угол наклона траектории в точке падения;

- дальность и полное время полета.

4. Построить графики: траектории, профиля скорости, проекций скорости и ускорений от времени.

Часть 2. Оптимизация траектории движения неуправляемого ла

В данной части лабораторной работы необходимо провести оптимизацию траектории полета неуправляемого ЛА, полученной в части 1, с точки зрения увеличения дальности.

1. Провести однопараметрическую оптимизацию траектории движения центра масс неуправляемого ЛА

• Выбрать не менее пяти параметров ЛА и начальных условий пуска.

• Изменяя каждый из выбранных параметров в пределах от 5 до 30% (при прочих равных условиях) определить изменение дальности.

• Построить зависимость дальности полета от величины изменяемого параметра.

• Проанализировать, как изменяется дальность полета ЛА (на сколько процентов) при изменении выбранных параметров, и выбрать наиболее целесообразный способ увеличения дальности.

2. Провести многопараметрическую оптимизацию траектории движения центра масс неуправляемого ЛА

• Изменяя одновременно три из выбранных для однопараметрической оптимизации параметра в пределах от 5 до 30% (при прочих равных условиях) определить изменение дальности.

• Проанализировать, как изменяется дальность полета ЛА при различных комбинациях выбранных параметров.

3. Увеличить дальность полета ЛА не менее чем на 25 %

• Используя результаты п.1 и п.2 выбрать способ увеличения дальности

• Построить две траектории оптимальную и исходную.

4. Сделать выводы по результатам оптимизации

Правила оформления отчета

Отчет оформляется на А4 в текстовом редакторе Word и должен содержать следующий разделы:

- титульный лист;

- исходные данные;

- теоретический материал;

- результаты расчета, графики;

- вывод по результатам.

Контрольные вопросы

1. Какая система координат, используется при расчете траектории?

2. Физическая модель полета неуправляемого ЛА?

3. Допущения, принятые при разработке математической модели?

4. Каким образом учитывается изменение силы лобового сопротивления от скорости ЛА?

5. Численный метод решения математической модели?

6. На какие участки делится траектория полета ЛА?

Лабораторная работа №2 Расчет траектории полета ЛА с участком планирования

Цель работы: рассчитать и построить траекторию ЛА с участком планирования; исследовать влияние различных параметров ЛА или начальных условий пуска на дальность полета.

Основы теории

Система уравнений движения

Система уравнений движения, положенная в основу математической модели движения ЛА по траектории с участком планирования, описывает как неуправляемый полет по баллистической траектории, так и управляемый полет на участке планирования (рисунки 3 и 4). Под планированием понимается поддержание постоянным определенного значения угла тангажа на конечном участке траектории. При этом уменьшается влияние силы тяжести на траекторию.

Рисунок 4 – Силы, действующие на ЛА

Неуправляемый полет ЛА по баллистической траектории описывается уравнениями (1)-(5) и (7)-(10). Уравнение (6) примет следующий вид:

, (6а)

где С_i - коэффициент индуктивного сопротивления, обусловленный наличием угла атаки.

, (11)

где - производная коэффициента подъемной силы по углу атаки, - угол атаки.

Для расчета участка планирования необходимо добавить следующие уравнения:

- для определения подъемной силы

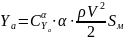, (12)

- закон изменения угла тангажа:

, (13)

где - угол тангажа.

Критическое значение угла атаки задается.

Таким образом уравнения (1)-(5), (6а), (7)-(13) полностью описывают движение ЛА по траектории с участком планирования с учетом принятых допущений.

Численная реализация данной системы уравнений осуществляется методом Эйлера, приведенным в лабораторной работе №1.