Контрольні запитання:

1. Як реалізуються розгалуження в ЕТ?

2. Призначення, формат, робота функції ЯКЩО?

3. Які ви знаєте логічні функції?

4. Яке призначення кнопки Автосумма?

5. Що таке абсолютна і змішана адреси клітинки?

6. Яка різниця між відносними і абсолютними адресами клітинок?

7. Як обчислити суму чисел у стовпці?

8. Як ввести дату в клітинку?

9. Який загальний вигляд має логічна функція І?

10. Який розділювач можна використовувати у списках аргументів функції?

11. Як відредагувати дане в клітинці?

12. Як вставити стовпець у таблицю?

13. Чи може бути функції ЯКЩО вкладеною?

14. Який загальний вигляд має логічна функція АБО?

15. Яка різниця між логічними функціями І та АБО?

16. Як вставити чисту сторінку у книжку?

17. Як очистити весь стовпець

18. Як вилучити рядок з таблиці?

19. Яку стандартну функцію заміняє кнопка Автосумма?

20. Як виокремити несуміжні діапазони клітинок?

21. В чому полягає метод підбору параметра?

22. Які задачі можна розв'язати методом підбору параметра.

23. Які є способи розв'язування нелінійного рівняння?

Завдання для дому:

Завдання 2а. Відповісти письмово:

23. Яке значення функції ЯКЩ0(1>2; 1; 2)? 24. Яке значення функції ЯКЩО(5=5. 4; 5)?

25.Яке значення функції І(2=2; 3=3; 3<4)? 26.Яке значення функції ЯКЩ0(2>1; 10; 20)?

27.Яке значення функції ЯКЩО(1=2; 15; 25)? 28.Яке значення функції АБО(1=2; 3=3; 4=5)?

29.Яке значення функції АБО(1=2; 3=3; 4=5)? 30.Яке значення ЯКЩО(5>2 5; 2)?

31.Яке значення функції ЯКЩО(3<5: 8; 12)? 32.Яке значення ЯКЩО(8>2; 2; 8)?

33.Яке значення функції ЯКЩО(2>1; ЯКЩО(1>2; 5; 8); 6)?

Завдання 2б: обчислити за допомогою ЕТ значення функції Y(x):

f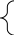 1(x), якщо x<=30,

Y=

f2(x), в інших випадках,

д е

f1(x)= |2sin x²|+11,8 cos (x/0,4-1)+ √(3+x)², f2(x)= sin²(x+3)-sin(5x+3)+cos²(x+3)³

(7x-30)+sin²5x

якщо значення аргументу х змінюються на відрізку [-3,3] з кроком 1

7