Пример решения задания 3
Рассмотрим пример расчета вала
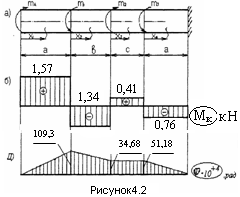
Для стального вала требуется:
1.Найти через известные мощности Рi,, сответствующие скручивающие моменты mi;
2.Найти известный момент mA из условия равенства нулю угла закручивания свободного конца вала;
3.Построить эпюру крутящих моментов Мк;
4.Подобрать круглое сечение из условия прочности;
5.Построить эпюру углов поворота .
Решение:
Заданная схема показана на рисунке 4.2.
Определяем скручивающие моменты:
;
;
.
2 Значение неизвестного момента mA найдем из того условия, что угол закручивания свободного конца вала равен нулю, т.е. А=0. Для удобства счета разобьем этот угол на составляющие, зависящие от каждого скручивающего момента, т.е. φА = φТА + φТ1 + φТ2 + φТ3 = 0 ,
где φТА - угол поворота концевого сечения от действия только момента ТА, φТ1- то же, но от действия только момента Т1;
φТ2 - от действия только момента Т2; φТ3 - от действия только момента Т3;
т.е.
Подставив числовые значения, после преобразований, получим
ТA = 1,57 кНм
Пользуясь методом сечений, определяем величины крутящих моментов на отдельных участках вала.
Участок 1 0 ≤Z1≤ а;
ТK1= +ТА = +1,57 кНм Участок 2 0 ≤ Z2 ≤ b;
ТК2= ТА –Т1= 1,57 - 2,91 = -1,34кНм Участок 3 0 ≤ Z3 ≤с;
ТK3 = ТА –Т1 + Т2= 1,57 - 2,91 +1,75 = 0,41кНм Участок 4 0 ≤ Z4 ≤а;
ТК4 = ТА –Т1+ Т2 – Т3 = 1,57 - 2,91 +1,75 -1,17 = -0,76кНм По полученным значениям крутящих моментов строим эпюру Tк .
4 Определим диаметр вала из условия прочности по максимальному крутящему моменту
,
где W=0,2 D3
Тогда
=
=6,4
см=64 мм округляя до стандартного, получаем
D=65 мм
5 Вычислим углы поворота «»
Участок 1: 0 z1 а=1 м
;
z1=0 z1=1,0 м
1=0 
рад.
Участок 2: 0 z2 в=0,8 м
z2=0 z2 = в=0,8 м=80 см
2=1=0,0109 рад
рад.
Участок 3 0 z3 0,6 м
;
z3=0; z3 с=0,6 м
3=2=34,6810-4
рад;
рад.
Участок 4 0 z4 а=1,0 м=100 см
;
z4=0; z4=100 см;
4=3=51,1810-4
рад;
По полученным значениям I строим эпюру углов поворота «» (рисунок 4.2).
Задание 4 Плоский изгиб балочных систем
Для заданной балки (рисунок 4.1) требуется:
1) построить эпюры поперечных сил Q, изгибающих моментов М;
2) подобрать;
- для балок с 1 по 6 схемы – из сортамента двутавровое сечение, материал балки – сталь []=160 МПа;
- для балок с 7 по 12 схемы – круглое сечение, материал балки – дерево []=10 МПа;
- для балок с 13 по 18 схемы - прямоугольное сечение с отношением сторон h:b=2, материал - сталь []=160 МПа;
Исходные данные в таблице 4.1
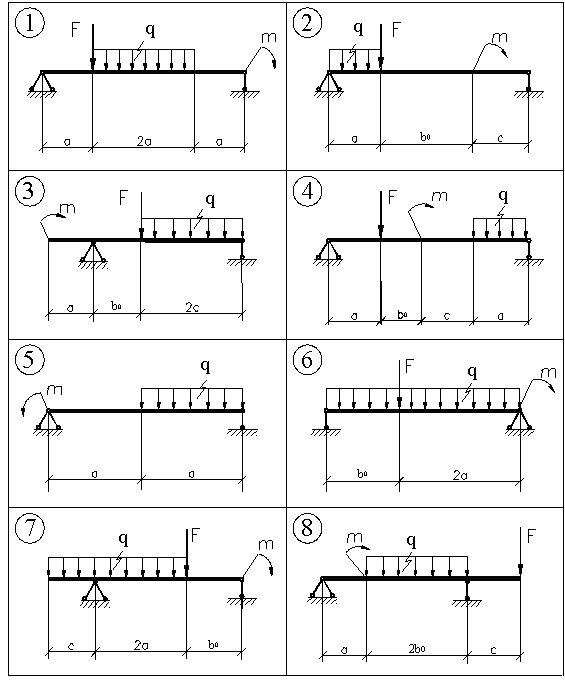
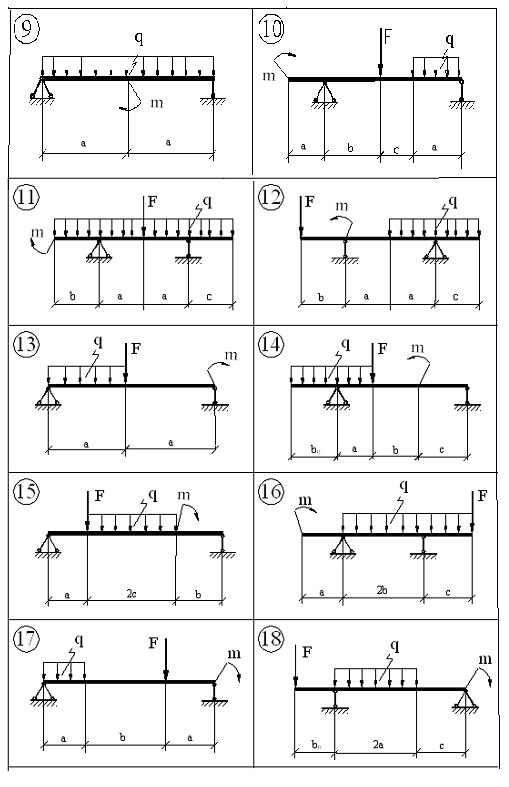
Р
исунок
4.1 -
Схемы балок
Таблица 4.1
№ п\п |
Нагрузка |
Длины участков, м |
||||
F, кН |
m, кНм |
q, кН/м |
a |
b |
c |
|
1 |
20 |
30 |
20 |
3 |
2 |
1 |
2 |
30 |
40 |
20 |
2 |
2 |
2 |
3 |
40 |
40 |
30 |
3 |
3 |
2 |
4 |
30 |
20 |
20 |
3 |
1 |
1 |
5 |
20 |
30 |
20 |
2 |
2 |
1 |
6 |
30 |
30 |
10 |
3 |
3 |
2 |
7 |
30 |
20 |
10 |
2 |
3 |
3 |
8 |
40 |
10 |
30 |
3 |
2 |
2 |
9 |
20 |
40 |
30 |
3 |
3 |
2 |
10 |
30 |
30 |
20 |
2 |
3 |
3 |
11 |
22 |
20 |
30 |
2 |
2 |
1 |
12 |
32 |
10 |
8 |
2 |
3 |
2 |
13 |
24 |
20 |
10 |
2 |
2 |
3 |
14 |
26 |
40 |
12 |
1 |
2 |
1 |
15 |
18 |
40 |
10 |
3 |
2 |
1 |
16 |
16 |
20 |
20 |
2 |
2 |
2 |
17 |
28 |
30 |
14 |
2 |
1 |
2 |
18 |
14 |
30 |
20 |
3 |
1 |
2 |