БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ "ВОЕНМЕХ"

им. Д. Ф. УСТИНОВА

Кафедра И3

КУРСОВАЯ работа

по учебной дисциплине: Стохастические системы управления_______________________________

на тему: Сокращение трудоемкости статистического моделирования__________________________

студента_______________Кордубайло Дениса Андреевича_______________________________

группы ____И351___________

ПРЕПОДАВАТЕЛЬ

Королев С.Н. / ______________ /

Подпись

“___" _________________ 2009 г.

САНКТ-ПЕТЕРБУРГ

2009 г.

Содержание

Содержание 2

Введение 3

3

Аналитическое решение 3

Стандартная схема статистического моделирования 5

Рациональная схема статистического моделирования 7

Приложение А 12

Приложение Б 13

Введение

Требуется определить математическое ожидание выходного сигнала X неустойчивого апериодического звена в заданный момент времени Т. Модель звена:

где ,

Данная модель звена содержит случайные параметры с равномерным законом распределения в заданных интервалах.

Допустимая абсолютная погрешность результата: .

Задачу решить тремя способами:

1. Используя стандартную схему статического моделирования;

2. Используя рациональную схему статистического моделирования с применением метода расслоенной выборки;

3. Аналитически.

Результаты аналитического решения использовать для проверки результатов статистического моделирования и для обоснования построения рациональной схемы моделирования.

Исходные данные для варианта 8:

G = 1 ,

a = 0.6-1.1 ,

T = 1,

A = 0,

k = 1 ÷ 1,5.

Метод снижения трудоемкости: метод расслоенной выборки.

Аналитическое решение

Проинтегрировали дифференциальное уравнение (1) методом Лагранжа[1]:

Так же проинтегрировали соответствующее (1) однородного дифференциального уравнения:

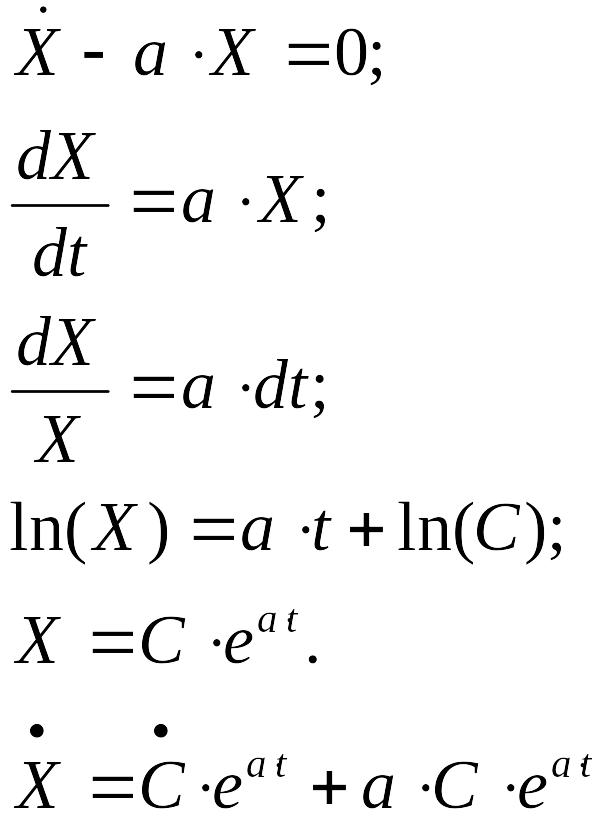
Подставили и в уравнение (1):

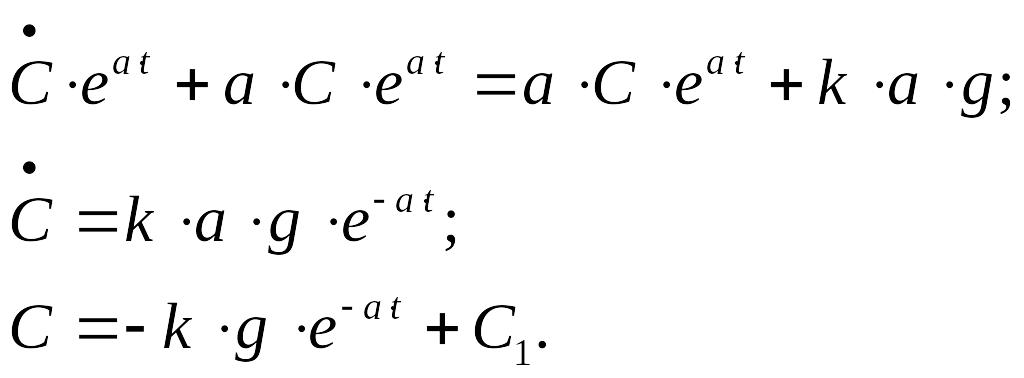
Нашли С₁ из начального условия X(0) = A:

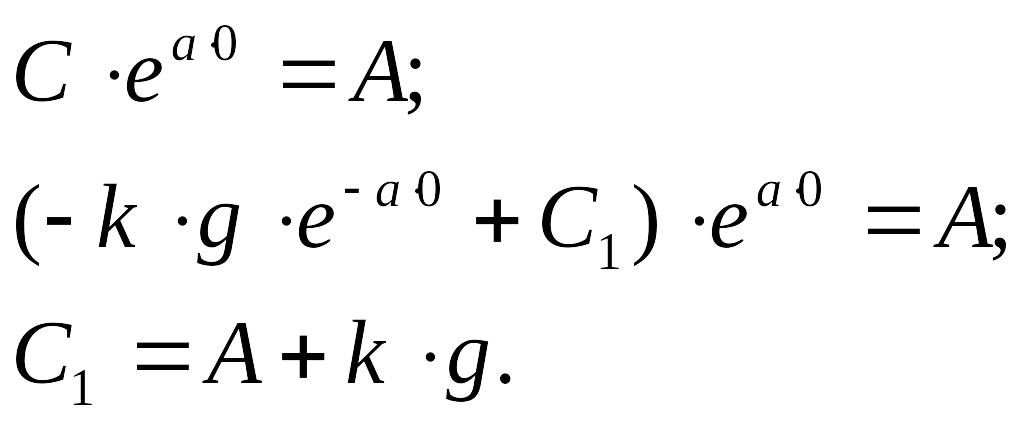
В результате получили:

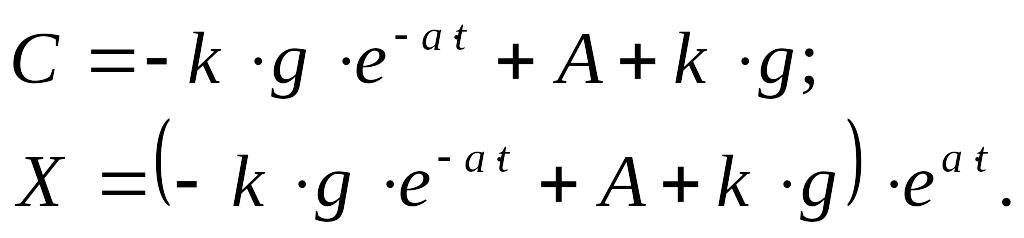
Решение исходного дифференциального уравнения (1) имеет вид:

Где

A =0,

k – случайный параметр, распределенный по равномерному закону в интервале [1;1,5].

Для Т = 1 с учетом статистической независимости A и k определили искомую характеристику:

где – искомое математическое ожидание.

С учетом (2) определили математическое ожидание в момент времени Т = 1:

Определили дисперсию :

Таким образом

С учетом известной дисперсии оценили необходимое количество опытов с погрешностью :

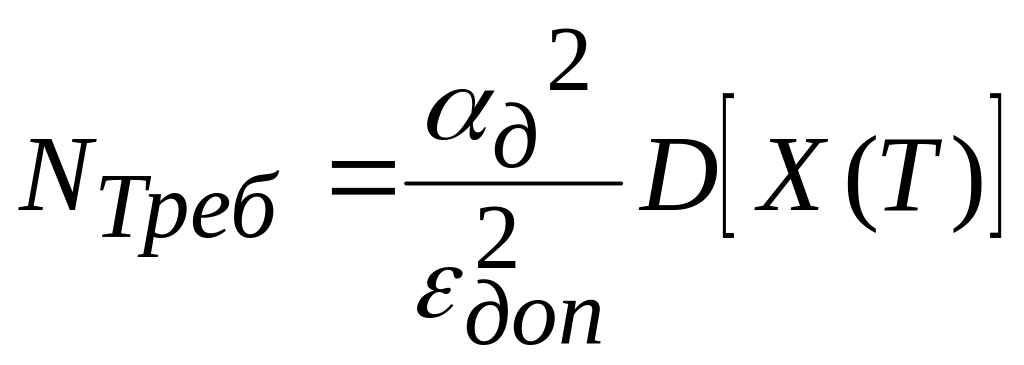
где – необходимое количество опытов.

Значение параметра зависит от доверительной вероятности . Примем =0,997 и

=3. Подставив значения параметров в (4), получили:

опытов.

Стандартная схема статистического моделирования

Если трудоемкость эксперимента имеет существенное значение, применяются итерационные алгоритмы получения оценок [2]. Идея итерационных алгоритмов состоит в том, что определение точности и требуемого количества опытов проводится в ходе эксперимента на основе получаемых оценок искомых параметров.

Блок-схема типового итерационного алгоритма приведена на рисунке 1.

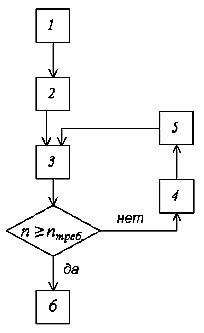
Рисунок 1 - Блок-схема итерационного алгоритма

Для задачи оценки математического ожидания случайной величины x предусматривается:

1. Проведение начальной серии опытов объемом n и накопление сумм

,

где - реализация случайной величины x в отдельных опытах.

2. Вычисление оценок математического ожидания и дисперсии :

3. Получение оценки требуемого количества опытов:

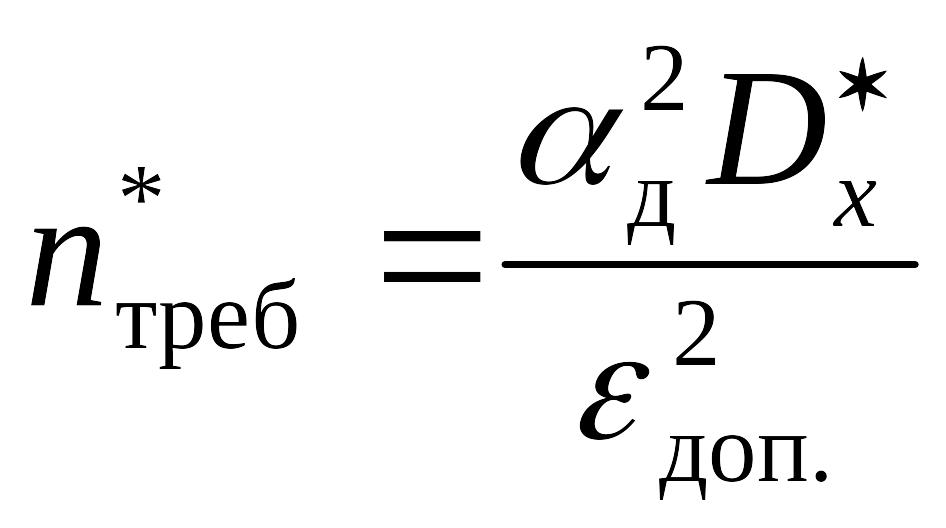
4. Проведение дополнительной серии опытов объемом и накопление сумм:

, .

5. Уточнение оценок математического ожидания m*x и дисперсии D*x:

При решении поставленной задачи численное интегрирование методом Эйлера первого порядка проводилось на ЭВМ в среде Matlab6.5 [2]. Программа, проводящая данные вычисления, представлена в приложении А.

В ходе реализации описанного алгоритма было проведено несколько серий опытов, результаты которых сведены в таблицу 1.

Таблица 1 – Результаты вычисления по стандартной схеме

Номер итерации				Количество проведенных опытов
1	1.515	0.334	30145	200
2	1.548	0.295	26588	1000
3	1.596	0.254	22897	3000
4	1.601	0.244	21973	5000
5	1.699	0.235	21219	9000
6	1.704	0.231	20859	12000
7	1.707	0.228	20573	15000
8	1.711	0.224	19800	19800

Таким образом, окончательным результатом реализации алгоритма являются следующие значения: , , .

Выигрыш составил : 30145/19800= 1.52 раза.

Проблема метода статистического моделирования связана с тем, что результаты проводимых серий опытов складываются случайным образом и при конечных n возможны следующие негативные эффекты:

• Выборочный закон распределения может существенно отличаться от нормального. Чаще всего оценки требуемого количества опытов оказываются завышенными.

• Разброс составляющих выборку реализаций случайной величины может оказаться существенно меньше истинного ее разброса. Оценки требуемого количества опытов оказываются резко заниженными, а результаты моделирования - неточными. Во избежание подобных ситуаций рекомендуется выбирать объем начальной серии опытов не менее 100-500.

• В выборке могут оказаться реализации случайной величины, значительно отличающиеся от ее среднего значения, в непропорционально большом количестве (возможны завышенные оценки требуемого количества опытов для получения точных результатов моделирования).