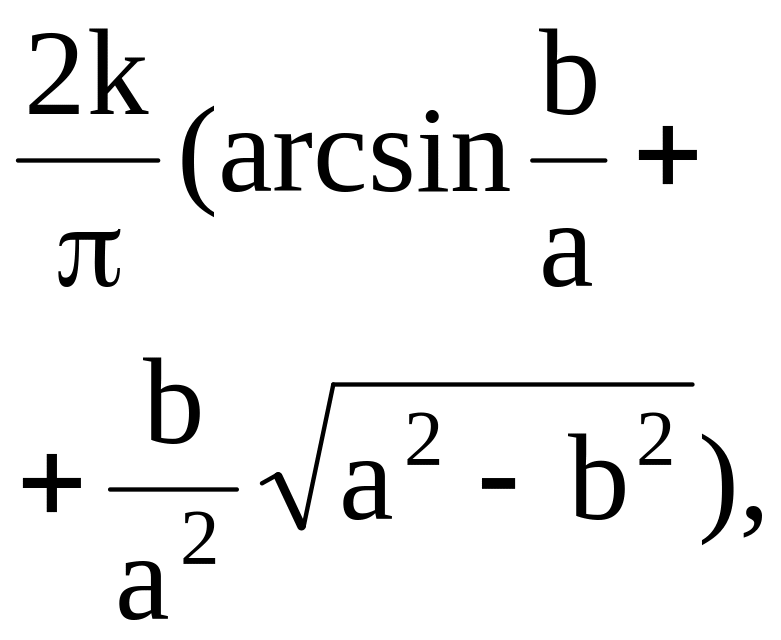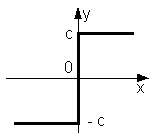
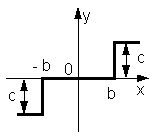
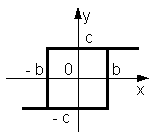
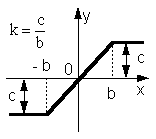
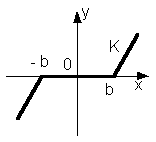
Коефіцієнти гармонічної лінеаризації типових нелінійностей

№
1			0
2			0
3
4			0
5			0

Із виразу (9.3) можна знайти відношення між y та x і назвати його еквівалентною передавальною функцією нелінійного елемента:

.

Для отримання частотної передавальної функції приймаємо , і тоді:

, (9.4)

тобто, еквівалентна частотна передавальна функція нелінійного елемента є функцією амплітуди і не залежить від частоти: .

Модуль еквівалентної передавальної функції показує відношення амплітуди першої гармоніки на виході до амплітуди вхідного сигналу, а аргумент - фазовий зсув між першою гармонікою виходу та вхідним синусоїдальним сигналом. Для однозначних характеристик , тобто вони не завдають запізнень за фазою.

Для розімкнутої системи можна записати:

. (9.5)

Якщо у замкнутій системі існують автоколивання, то . Тоді

, (9.6)

. (9.7)

Останнє рівняння є рівнянням гармонічного балансу, яке характеризує умови виникнення автоколивань. Роз’вязувати його можна різними методами, але найбільш розповсюдженим є графоаналітичний метод Гольдфарба (метод був запропонований 1944 року одночасно Гольдфарбом (СРСР) і Кохенбургером (США)).

З а цим методом на комплексній площині будують АФЧХ лінійної частини системи і обернену гармонічну характеристику нелінійного елемента (рис.9.5).

Якщо ці годографи перетинаються, то у досліджуваній системі можливі автоколивання. Параметри автоколивань при цьому легко визначити, оскільки має частотні позначки, а характеристика - амплітудні. Якщо характеристики не перетинаються, то автоколивання відсутні.

При цьому слід пам’ятати правило: якщо, рухаючись по кривій у сторону збільшення амплітуди, ми виходимо з контуру, охопленого , то точці перетину відповідають стійкі коливання (точка Д), а якщо входимо (точка С) – нестійкі (рис. 9.5). Точка Д визначає параметри автоколивань.

Слід пам’ятати, що даний метод є наближеним, оскільки вважається, що лінійна частина системи є фільтром низьких частот.

9.4 Порядок виконання роботи

Д ослідженню підлягає нелінійна система автоматичного керування, до складу якої входить лінійна частина (ЛЧ) і нелінійний елемент (НЕ) (рис. 9.6).

Передавальна функція ЛЧ має вигляд:

W(s) = К/[s(Т₁s + 1)(Т₂s + 1)]. (9.8)

Значення коефіцієнта підсилення К та сталих часу Т₁ і Т₂ наведені в таблиці 9.2. У таблиці також задано вид і параметри статичної характеристики нелінійного елемента.

Таблиця 9.2

Завдання до лабораторної роботи

№ варіанта	1	2	3	4	5
К,с-1	5	10	15	10	15
Т1,с	0.5	0.1	0.05	0.05	0.04
Т2,с	0.01	0.05	0.01	0.2	0.1
Тип НЕ (№ за табл. 9.1)	3	4	1	5	2
b			-
c				-

9.4.1 Відповідно до свого варіанту виконати за допомогою пакета Matlab моделювання нелінійної системи (рис. 9.6), за умови f=0.

9.4.2 У разі виникнення автоколивань визначити їх амплітуду й частоту, побудувавши для цього перехідний процес і фазовий портрет системи (див. лабораторну роботу №8). Зробити висновки.

9.4.3 Якщо автоколивання не виникають без зовнішньої дії, подати на вхід системи короткий імпульс певної амплітуди. Змінюючи цю амплітуду, зафіксувати, за якої величини імпульсу автоколивання виникають. Виконати пункт 9.4.2.

9.4.4 Дослідити систему методом Гольдфарба [4, приклад 7.2]. Побудову АФЧХ лінійної частини системи і оберненої гармонічної характеристики нелінійного елемента можна виконувати за допомогою пакета MathCad. Порівняти отримані результати з результатами моделювання. Зробити висновки.

9.4.5 Кінець роботи.