16.4 Интерполирующие цифровые фильтры
Интерполяцией называется увеличение частоты дискретизации сигнала. Отношение количества выходной частоты дискретизации сигнала к входной частоте дискретизации сигнала называется коэффициентом интерполяции. Обычно коэффициент интерполяции выбирается целым числом.
При увеличении частоты отсчетов цифрового сигнала, в соответствии с теоремой Котельникова расширяется полоса частот, описываемых этими отсчетами. Это означает, что в новую полосу частот попадает несколько частотных образов первоначального варианта сигнала. При выполнении операции интерполяции необходимо выбрать нужный частотный образ. Обычно выбирается полоса частот от 0 до fв (низкочастотный образ сигнала).
Задача выбора необходимого частотного образа решается при помощи цифрового фильтра. Такой фильтр называется интерполирующим. Именно этот фильтр вычисляет значения сигнала в точках между первоначальными отсчетами.
Интерполирующий фильтр с конечной импульсной характеристикой
Рассмотрим пример первоначального представления сигнала во временной области. Пример временной реализации исходного сигнала приведен на рисунке 16.8.
Рисунок 16.8 – Пример временной реализации сигнала
На данном рисунке отсчеты полезного сигнала обозначены кружочками, а для того чтобы легче было представить форму исходного сигнала, они соединены прямыми линиями. При интерполяции сигнала требуется увеличить количество его отсчетов в единицу времени. При интерполяции новые отсчеты сигнала заполняются нулевыми значениями, как это показано на рисунке 16.9.
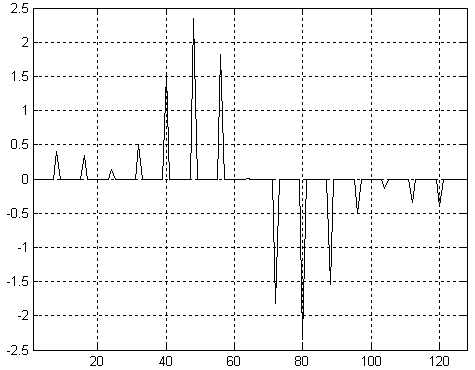
Рисунок 16.9 – Сигнал на входе интерполирующего фильтра
Здесь я хотел бы подчеркнуть, что промежуточные отсчеты должны быть заполнены именно нулями. Если их заполнить другими значениями, например повторениями предыдущего отсчета сигнала, то уровень высокочастотных составляющих спектра значительно уменьшится. Казалось бы это облегчит работу интерполирующего фильтра, однако при этом будет искажен и сигнал в интересующей нас полосе частот.
Более того, станет невозможным применять в качестве фильтра-интерполятора фильтры Найквиста, так как будет невозможно получить нулевое значение межсимвольной интерференции между соседними символами в отсчетных точках сигнала.
Спектр цифрового сигнала, изображенного на рисунке 16.9, приведен на рисунке 16.10. На графике четко прослеживается повторяющийся характер его спектра. Теперь, для того, чтобы осуществить интерполяцию этого сигнала, необходимо подавить его нежелательные спектральные компоненты, расположенные на частоте высокочастотных образов входной частоты fд исходного сигнала.
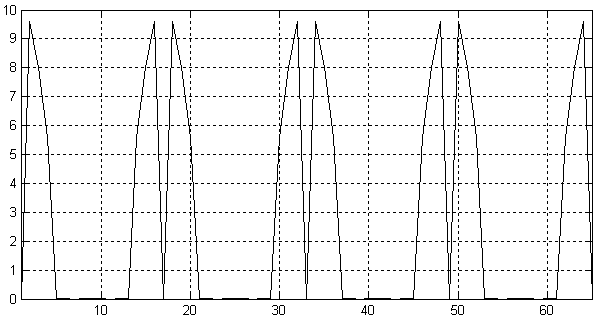
Рисунок 16.10 – Спектр сигнала, приведенного на рисунке 15.9
Подавим все высокочастотные составляющие спектра сигнала при помощи цифрового фильтра нижних частот. Для этого зададимся уровнем подавления высокочастотных составляющих спектра равным –75 дБ. Это эквивалентно 12‑разрядному представлению полезного сигнала. Такой уровень подавления высокочастотных составляющих спектра можно реализовать при помощи цифрового нерекурсивного фильтра со 128 отводами.
Получившаяся в результате расчета амплитудно-частотная характеристика интерполирующего фильтра с конечной импульсной характеристикой при использовании шестнадцатиразрядных весовых коэффициентов приведена на рисунке 16.11.
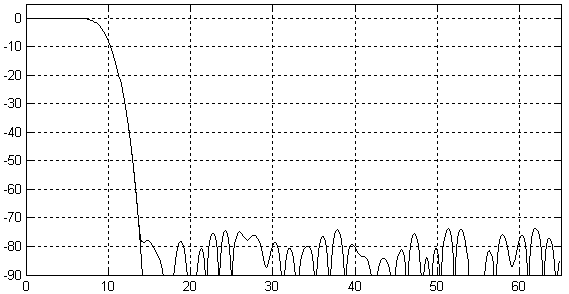
Рисунок 16.11 – Амплитудно-частотная характеристика интерполирующего фильтра
В полосе пропускания такой фильтр обеспечивает неравномерность коэффициента передачи на уровне 0,001 дБ. Таким образом, учитывая, что фильтр с симметричной импульсной характеристикой обладает линейной фазовой характеристикой, разработанный фильтр практически не вносит искажений в исходный сигнал.
Сигнал, показанный на рисунке 16.9, при прохождении через фильтр с амплитудно-частотной характеристикой, приведенной на рисунке 16.11, принимает вид, изображенный на рисунке 16.12. Обратите внимание, что сигнал на выходе фильтра будет задержан на время, равное групповой задержке фильтра. Для фильтра с конечной импульсной характеристикой это время равно частоте дискретизации выходного сигнала, умноженной на половину количества отводов фильтра.
На рисунке 16.12 приведено 128 временных отсчетов сигнала на выходе фильтра. Они практически сливаются друг с другом, поэтому отдельные отсчеты не выделяются кружочками, как это было сделано на рисунке 16.8. Как видно из приведенного на рисунке графика, сигнал на выходе фильтра практически не отличается от исходного (существовавшего до дискретизации) сигнала.
Рисунок 16.12 – Сигнал на выходе интерполирующего фильтра
При разработке интерполирующего фильтра следует обращать внимание, что, так как реальный фильтр всегда имеет конечную крутизну ската своей амплитудно-частотной характеристики, то полоса частот сигнала, подлежащего интерполяции всегда должна быть меньше половины частоты дискретизации. Только в этом случае интерполяция исходного цифрового сигнала может быть выполнена без искажений.
Теперь рассмотрим, как будет выглядеть этот же сигнал, если из исходного сигнала выделить не нулевой, а первый частотный образ сигнала. Получившийся на выходе полосового фильтра сигнал приведен на рисунке 16.13. Для сравнения на этом же рисунке приведен низкочастотный (нулевой) образ сигнала.
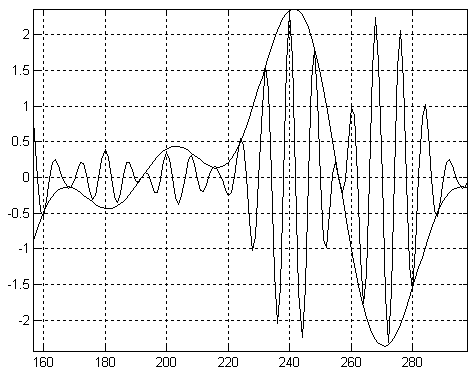
Рисунок 16.13 – Сигнал на выходе интерполирующего фильтра
На рисунке отчетливо видно, что исходные значения сигнала совпадают как в низкочастотном, так и в первом образе сигнала. В момент пересечения нулевого значения фаза несущей частоты первого образа меняет свой знак. Точно так же вели бы себя и второй и третий образ сигнала. Отличие заключается только в значении несущей частоты.
Применение для формирования несущей частоты высокочастотных образов первоначального сигнала неудобно, так как в этом случае можно реализовать всего несколько фиксированных частот. Намного удобнее для переноса спектра исходного сигнала на несущую частоту использовать схему квадратурного модулятора, приведенную на рисунке 3.6. Эта схема позволяет переносить спектр исходного сигнала на любую частоту, не превышающую половину частоты дискретизации.
Интерполяция обычно производится в несколько этапов. Первые два этапа обычно обеспечивают увеличение скорости отсчетов сигнала в два раза каждый. Это связано с тем, что первоначально почти вся полоса частот от 0 до fд/2 занята полезным сигналом, т.е. полезный сигнал и его высокочастотные образы находятся близко друг от друга. В результате от интерполирующего фильтра требуется высокая крутизна ската амплитудно-частотной характеристики и для его реализации требуется большое количество отводов и коэффициентов.
После выполнения этих первых двух этапов интерполяции полезный сигнал занимает только 25% полосы частот. В результате требования к избирательности фильтра уменьшаются, а значит, последующий интерполирующий фильтр может обеспечить больший коэффициент интерполяции.
Параллельная реализация интерполирующего фильтра с конечной импульсной характеристикой.
Для реализации фильтра с конечной импульсной характеристикой обычно требуется несколько десятков отводов отводов от цифровой линии задержки. При интерполяции это становится определяющим фактором, ведь при увеличении количества отводов уменьшается быстродействие цифрового фильтра! А в результате интерполяции частота дискретизации возрастает и быстродействие фильтра становится определяющим значением.
Неужели в интерполирующих фильтрах придется использовать прямую реализацию цифрового фильтра с конечной импульсной характеристикой? Сколько же тогда будет потреблять наша микросхема! Однако не так все страшно. Давайте вспомним, что в интерполирующем фильтре большинство входных отсчетов являются нулями.
Получается, что большую часть производительности нашей микросхемы мы будем тратить на умножение на ноль! Неплохо … для тех, кому заняться нечем!
Итак, у нас появилась реальная возможность уменьшить количество операций, которые необходимо выполнить в период между импульсами выходной дискретизации. Получается, что нам следует умножать на весовые коэффициенты фильтра только те отсчеты входного сигнала, которые в данный момент не равны нулю.
Но как же это сделать? Ведь каждый отсчет последовательно проходит через все весовые коэффициенты. Рассмотрим пример интерполирующего фильтра на основе полуполосного фильтра.
Частоту дискретизации на выходе этого фильтра можно только удвоить по отношению к входной частоте, поэтому в данном фильтре каждый второй отсчет в линии задержки содержит ноль. Тогда все весовые коэффициенты фильтра можно разбить на две части — четную и нечетную.
Расположим эти части в постоянном запоминающем устройстве последовательно друг за другом. В результате у нас получились как бы два фильтра с длиной, в два раза меньшей по сравнению с исходным фильтром. При этом фильтры будут выдавать свои отсчеты на выход по очереди. Сначала один, а затем другой.
Что интересно, то для обоих фильтров можно воспользоваться одной и той же линией задержки, только сдвиг в этой линии задержки следует делать только после того, как отработают все фильтры. Для реализации этого фильтра можно воспользоваться структурной схемой нерекурсивного фильтра, приведенной на рисунке 15.35.
Повторим эту схему на рисунке 16.14. Для реализации новых принципов работы потребуются небольшие изменения. Прежде всего, так как длина линии задержки уменьшается вдвое, то коэффициент счета счетчика Сч1 будет равен N/2. В результате за N+1 импульс тактовой частоты этот счетчик успеет совершить два оборота.
Рисунок 16.14 – Структурная схема цифрового интерполирующего фильтра
В качестве еще одного преимущества данной схемы следует отметить то, что нулевые значения в фильтр-интерполятор заносить уже не требуется.
Рассмотренные принципы позволяют реализовать фильтр-интерполятор с любым коэффициентом интерполяции, однако на последних стадиях интерполяции обычно используют однородные интерполирующие фильтры, которые обладают наиболее простой структурой и максимальным быстродействием.
Давайте рассмотрим подробнее особенности реализации интерполирующих однородных фильтров.
Интерполирующий однородный фильтр.
Наиболее просто в цифровом виде реализовать рассмотренный нами ранее однородный фильтр, так как для его реализации не требуются цифровые умножители. Для однородного фильтра седьмого порядка формула выглядит следующим образом:
(3.3)
Структурная схема фильтра, реализующего формулу 3.1, приведена на рисунке 16.15.
Рисунок 16.15 – Структурная схема однородного фильтра седьмого порядка
При реализации такого фильтра потребуется 6 сумматоров. Во столько же раз уменьшится быстродействие цифрового фильтра. Можно несколько видоизменить структуру данного фильтра. Для сокращения количества выполняемых операций формула 3.3 может быть переписана в следующем виде:
(3.4)
Эта формула может быть реализована за два действия:
(3.5)
В таком случае для реализации однородного фильтра потребуется два каскада. Второй каскад будет выполнять интегрирование, а первый — фильтр с конечной импульсной характеристикой всего с двумя ненулевыми коэффициентами, равными единице. Новая структурная схема однородного фильтра приведена на рисунке 16.16.
Рисунок 16.16 – Структурная схема двухкаскадного фильтра, эквивалентного фильтру, приведенному на рисунке 16.15
В этой схеме максимальное время задержки сигнала определяется быстродействием сумматора и временем записи в регистр. Мы увеличили быстродействие схемы почти в семь раз.
Ну а теперь вспомним, что анализируемый фильтр работает при частоте дискретизации сигнала в N раз выше частоты дискретизации входного сигнала. В этом случае для формирования того же самого значения времени задержки до увеличения частоты дискретизации нам потребуется всего только один регистр, так как на его вход тактовой синхронизации будет поступать частота, в шесть раз меньше, чем частота синхронизации на выходе интерполирующего фильтра.
Это означает, что имеет смысл тактировать первую часть фильтра входной частотой дискретизации. Получившаяся в результате всех описанных выше преобразований структурная схема однородного фильтра-интерполятора приведена на рисунке 16.17.
Рисунок 16.17 – Структурная схема фильтра-интерполятора, эквивалентного фильтру, приведенному на рисунке 16.16.
Новая схема содержит всего два регистра и два двоичных сумматора, то есть данная схема получилась в три раза проще схемы однородного фильтра, приведенной на рисунке 16.15.
Получившийся в результате преобразований фильтр трудно назвать однородным, однако для того, чтобы отобразить особенности его импульсной и амплитудно-частотной характеристик, сохраним название “однородный” и для этого фильтра. В иностранной литературе такой фильтр получил название CIC-фильтр.
Если по техническому заданию требуется еще больший коэффициент интерполяции по сравнению с рассмотренным выше случаем, то выигрыш при реализации однородного фильтра-интерполятора по схеме, приведенной на рисунке 16.17, будет еще большим.
Хотелось бы напомнить, что при анализе характеристик однородного фильтра для получения приемлемого уровня подавления мешающего сигнала нам потребовалось включить друг за другом несколько каскадов.
Давайте включим последовательно друг за другом три фильтра-интерполятора, как это показано на структурной схеме фильтра, приведенной на рисунке 16.18.
Рисунок 16.18 – Структурная схема трехкаскадного фильтра-интерполятора (CIC3).
На рисунке 16.19 приведена амплитудно-частотная характеристика четырехкаскадного однородного фильтра. Обратите внимание, что образ полезного сигнала сосредоточен около частоты дискретизации исходного сигнала x(t). Проанализировав амплитудно-частотную характеристику четырехкаскадного однородного фильтра можно определить, что этот фильтр в полосе частот высокочастотных образов полезного сигнала может обеспечить подавление мешающих сигналов до 90 дБ, что эквивалентно 16-разрядному представлению полезного сигнала. На приведенном рисунке черным цветом закрашена область частот, которая подавляется однородным интерполирующим фильтром. Остальные частоты (там, где находятся максимумы в полосе подавления однородного фильтра) были подавлены ранее полуполосными интерполирующими фильтрами.
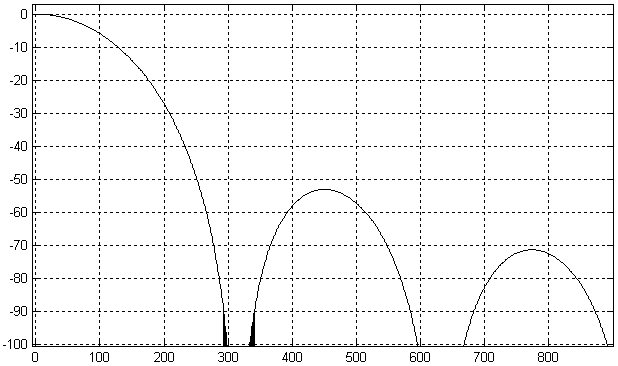
Рисунок 16.19 – Амплитудно-частотная характеристика четырехкаскадного однородного фильтра-интерполятора.
На этом закончим обзор особенностей реализации интерполирующих цифровых фильтров.
В заключение я хотел бы привести результирующую структурную схему цифрового квадратурного модулятора, на вход которой можно подавать цифровой поток с частотой отсчетов, в несколько раз более низкой по отношению к требующейся для формирования выходного радиосигнала. В этой схеме на входе умножителей используются интерполирующие фильтры. Схема цифрового квадратурного модулятора приведена на рисунке 16.20.
Рисунок 16.20 – Структурная схема квадратурного модулятора с низкоскоростным потоком квадратурных сигналов