15.5 Цифровые фильтры
Следующим, широко используемым блоком в схемах цифровой обработки сигналов являются цифровые фильтры. Прежде чем начать подробное обсуждение вопросов реализации цифровых фильтров давайте вспомним — что же такое частотные фильтры? Частотные фильтры требуются для подавления мешающих сигналов, отличающихся по частоте от полезного. В частотной области зависимость коэффициента передачи фильтра можно изобразить так, как это приведено на рисунке 15.28.
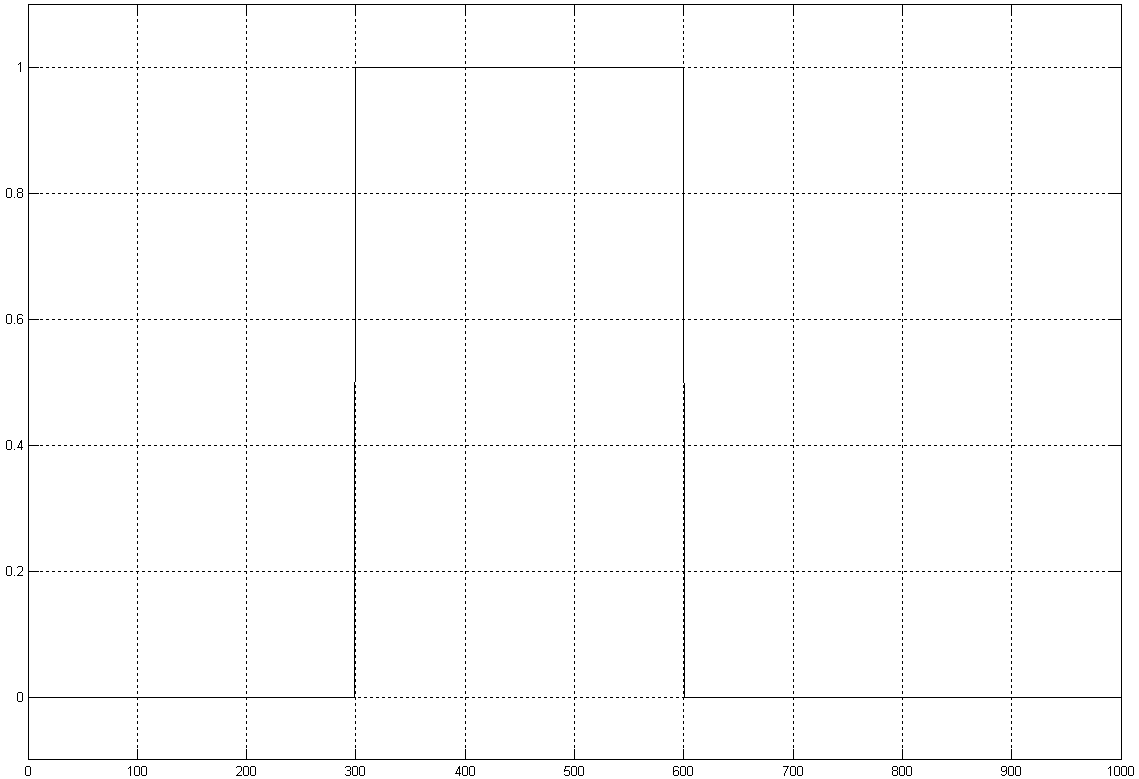
Рисунок 15.28 – Амплитудно-частотная характеристика коэффициента передачи фильтра
На этом рисунке приведена частотная характеристика фильтра, выделяющего нужную нам полосу частот. Однако мы знаем, что операция фильтрации (выделения полезной части данных) в частотной области эквивалентна операции вычисления свёртки во временной области и наоборот:
(15.1)
где S(f) — спектр сигнала;
s(t) — временная реализация сигнала;
G(f) — частотная характеристика полосового фильтра;
g() — импульсная характеристика полосового фильтра;
L — длина импульсной характеристики полосового фильтра.
Таким образом, для реализации фильтра нам достаточно определить форму импульсной характеристики фильтра и вычислить операцию свертки. Импульсная характеристика связана с частотной характеристикой преобразованием Фурье. Поэтому в простейшем случае рассчитать цифровой фильтр можно, используя преобразование Фурье от требуемой частотной характеристики.
Кроме знания формы импульсной характеристики для создания цифрового фильтра нам требуется уметь запоминать значения входного сигнала в предыдущие моменты времени. Для этого могут быть использованы параллельные регистры, внутреннее устройство которых рассмотрено в предыдущих главах. В формуле вычисления свертки используется арифметическая операция умножения. Устройство, способное выполнять эту операцию мы уже рассматривали в предыдущих главах.
Остается операция интегрирования. Однако при использовании целочисленных значений входного сигнала ее можно представить как сумму всех отсчетов этого сигнала, а внутреннее устройство арифметического сумматора мы уже знаем. При замене операции интегрирования суммой формула (15.1) примет следующий вид:
(15.2)
Рассмотрим структурную схему устройства, способного вычислять операцию свёртки (цифровой фильтр). Структурная схема цифрового фильтра приведена на рисунке 15.29.
fт
Рисунок 15.29 – Структурная схема устройства, способного вычислять операцию свёртки
В качестве элементов задержки в этой схеме использованы схемы параллельных регистров. Разрядность этих регистров определяет динамический диапазон входного сигнала. Если мы собираемся работать с динамическим диапазоном сигнала равным 96 дБ, то разрядность параллельных регистров должна составлять N = 96 дБ/6 дБ = 16 разрядов.
Точно такой же должна быть разрядность весовых коэффициентов фильтра. Это означает, что в составе схемы цифрового фильтра необходимо использовать умножители 16×16. Разрядность произведения при этом будет равна 32 разрядам. Суммирование сигналов со всех отводов линии задержки, реализованной на параллельных регистрах, производится двухвходовыми сумматорами. Их разрядность должна быть, по крайней мере, на восемь разрядов больше разрядности произведения содержимого регистров на весовые коэффициенты. То есть разрядность сумматоров должна быть равной 40 разрядам.
Давайте проверим, как будет реагировать приведенное на рисунке 15.29 устройство на одиночный импульс единичной амплитуды, поданный на его вход. Для наглядности рассуждений возьмем импульсную характеристику одиночного колебательного контура. Эта характеристика приведена на рисунке 15.30.
Рисунок 15.30 – Форма импульсной характеристики колебательного контура
На рисунке 15.30 кружочками обозначены значения весовых коэффициентов импульсной характеристики цифрового фильтра. Именно эти коэффициенты подаются на входы умножителей в структурной схеме цифрового фильтра, приведенной на рисунке 15.29. Для наглядности эти коэффициенты на рисунке соединены между собой прямыми линиями (так характеристика становится более похожей на импульсную характеристику аналогового колебательного контура).
Частотную характеристику фильтра, обладающего импульсной характеристикой, соответствующей рисунку 15.30, можно получить, проведя преобразование Фурье над этой импульсной характеристикой. Полученная в результате этого преобразования амплитудно-частотная характеристика фильтра приведена на рисунке 15.31. По оси абсцисс на этом рисунке отложена частота в килогерцах, а по оси ординат — коэффициент передачи цифрового фильтра в децибелах.
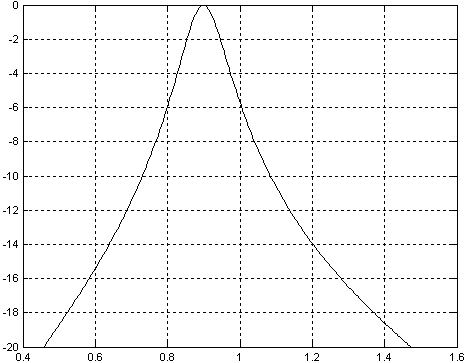
Рисунок 15.31 – Форма частотной характеристики фильтра
Теперь подадим на вход схемы, приведенной на рисунке 15.29, цифровой код, соответствующий единичному уровню сигнала. В первый момент времени во всех внутренних регистрах фильтра содержатся нулевые значения. Это означает, что при умножении этих значений на весовые коэффициенты мы получим в результате нули. Отличаться будет только результат на выходе первого умножителя. При перемножении весового коэффициента g0 на единичное значение входного сигнала мы получим на выходе умножителя значение сигнала с амплитудой g0.
Как мы уже знаем из предыдущих глав, задержка в схеме определяется частотой тактового сигнала, подаваемого на входы синхронизации параллельных регистров. При поступлении первого тактового импульса код, присутствовавший на входе схемы, запишется в первый регистр (элемент задержки). По этому же тактовому сигналу содержимое первого регистра (нулевое значение) перепишется во второй регистр, содержимое второго регистра перепишется в третий регистр и т.д.
Как мы договорились, теперь на вход фильтра мы подадим код, соответствующий нулевому значению сигнала. В результате на выходе всех умножителей, кроме второго умножителя, снова будет присутствовать нулевой код. Так как в первом регистре на этот раз содержится единичное значение, то в результате умножения на коэффициент g1, на выходе второго умножителя мы получим значение сигнала с амплитудой g1.
При поступлении последующих тактовых импульсов процесс будет повторяться, и мы на выходе схемы последовательно будем получать значения сигналов, соответствующие весовым коэффициентам.
Итак, мы убедились, что схема ведёт себя подобно обычному фильтру, и научились рассчитывать весовые коэффициенты этой схемы, требуемые для получения заданных характеристик фильтров. Собственно говоря, было бы удивительно не получить фильтр, ведь обычные аналоговые схемы фактически работают так же. Энергия на колебательном контуре постепенно накапливается за счет суммирования текущего входного напряжения и всех предыдущих значений, активный RC фильтр с обратными связями ведет себя точно так же.
Преимуществом рассмотренной схемы является то, что в ней мы можем выбирать коэффициенты импульсной характеристики произвольным образом без ограничений, которые обычно существуют в других видах фильтров. В результате этой особенности мы можем получить исключительные свойства, нереализуемые в других схемах.
Например, мы можем получить строго симметричную импульсную характеристику фильтра, подав на умножители коэффициенты, соответствующие этой импульсной характеристике. Таким образом, как это известно из теории линейных цепей, можно реализовать фильтр со строго линейной фазовой характеристикой, или, что то же самое, одинаковое время задержки фильтра во всей полосе рабочих частот. Это свойство чрезвычайно полезно для аппаратуры передачи данных или обработки телевизионных сигналов.
В качестве еще одного примера использования рассмотренной ранее схемы можно назвать реализацию фильтров Найквиста. Как известно, в этих фильтрах импульсная характеристика должна принимать нулевые значения строго через определенные интервалы, равные длительности передаваемого символа. И такая возможность нам доступна — кто же может запретить нам записать в нужные ячейки памяти коэффициентов нулевой двоичный код?
Снова зададимся вопросом: как же рассчитывать цифровые фильтры? Простейший метод расчета этих фильтров мы рассмотрели выше по тексту. Это выполнение дискретного преобразования Фурье над заданной амплитудно-частотной характеристикой. Однако при решении инженерных задач осуществлять каждый раз преобразование Фурье достаточно трудоемкая задача.
Кроме того, для получения приемлемых результатов, полученную таким образом импульсную характеристику фильтра нужно обрабатывать временными окнами. При этом в каждом конкретном случае оптимальное с точки зрения получения заданной амплитудно-частотной характеристики решение может различаться. Более того, кроме метода преобразования Фурье существуют другие методы расчета цифровых фильтров. Подчас эти методы приводят к более эффективным решениям.
Для решения инженерных задач имеет смысл воспользоваться специализированными программами расчета цифровых фильтров. В качестве примера подобных программ можно привести такие программы, как FGEN или FILTER DESIGN, входящую в состав программной среды MATHLAB 6.12. Внешний вид рабочего окна программы FILTER DESIGN приведен на рисунке 15.32.
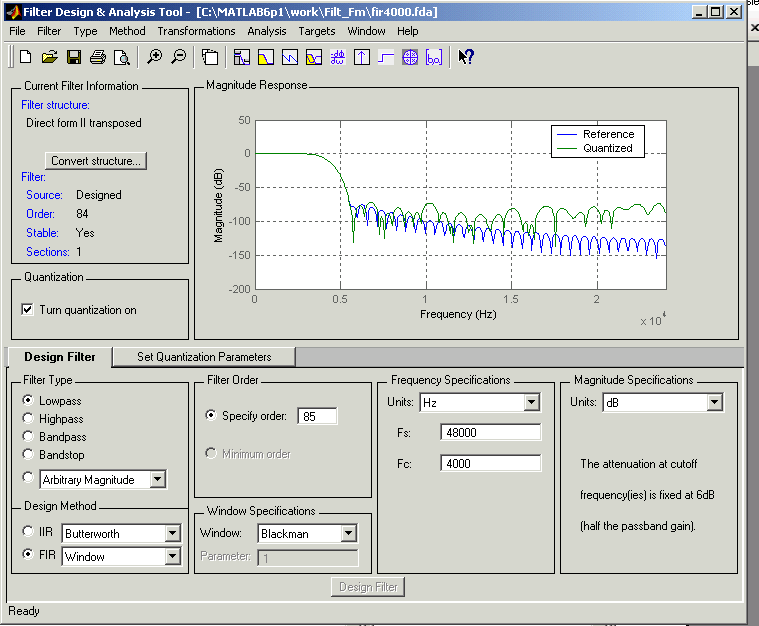
Рисунок 15.32 – Внешний вид программы FILTER DESIGN
Схемная реализация нерекурсивного фильтра
Теперь снова вернемся к схемотехнической реализации цифровых фильтров. В схеме, приведенной на рисунке 14.25, используется столько умножителей, сколько используется коэффициентов для реализации цифрового фильтра.
Обычно цифровые фильтры с произвольной импульсной характеристикой реализуются на частотах в несколько раз меньших предельной частоты работы цифровых микросхем. В этом случае вычисление результатов произведения всех весовых коэффициентов на задержанные значения входного сигнала для формирования одного выходного отсчета цифрового фильтра можно выполнить на одиночном цифровом умножителе и сумматоре.
Чтобы понять, как реализовать предложенный принцип вычислений, давайте рассмотрим подробнее структурную схему цифрового фильтра с конечной импульсной характеристикой. На рисунке 15.33 пунктиром показана повторяющаяся часть структурной схемы фильтра. А раз она повторяется, то эту часть схемы при вычислении выходного отсчета сигнала можно использовать многократно.
Рисунок 15.33 – Структурная схема цифрового фильтра седьмого порядка
Для запоминания промежуточных результатов суммирования нам потребуется дополнительный регистр. Так как в этом регистре результаты умножения отсчетов входного сигнала на весовые коэффициенты фильтра как бы накапливаются, то этот регистр получил название аккумулятор (накопитель). Вся же схема, осуществляющая математическую обработку сигнала при реализации цифрового фильтра, получила название умножителя-аккумулятора (MAC).
Давайте перерисуем структурную схему цифрового фильтра с конечной импульсной характеристикой, приведенную на рисунке 15.33, так, как это показано на рисунке 15.34.
Так как в качестве примера мы выбрали фильтр с конечной импульсной характеристикой седьмого порядка, то для синхронизации этой схемы потребуется частота, в семь раз большая частоты дискретизации входного (и выходного) сигнала.
Данные на входы умножителя-аккумулятора поступают с выходов кольцевых многоразрядных регистров. После поступления на вход синхронизации схемы семи тактовых импульсов, данные совершают полный круг и возвращаются на свое первоначальное место. В этот момент в аккумуляторе содержится вычисленное значение отсчета выходного сигнала фильтра.
Рисунок 15.34 – Структурная схема цифрового фильтра седьмого порядка
В следующий момент времени следует обнулить значение аккумулятора, подключить вход сдвигового регистра к входу x(t) и подать еще один тактовый импульс. Этот импульс позволит записать новое значение входного сигнала в первый параллельный регистр кольцевого многоразрядного регистра и осуществить перезапись содержимого всех остальных регистров в соседнюю ячейку (сдвинуть данные на одну позицию).
Цепи, осуществляющие эти действия в схеме, приведенной на рисунке 15.34, не показаны для того, чтобы не затенять основную схему. Теперь обратим внимание, что на этот раз (в отличие от схемы, приведенной на рисунке 15.33) нам не нужны все выходы параллельных регистров одновременно, поэтому для реализации кольцевого регистра можно воспользоваться оперативным запоминающим устройством (ОЗУ).
Весовые коэффициенты фильтра при этом будут находиться в ПЗУ. Схема цифрового нерекурсивного фильтра с использованием в качестве кольцевых регистров ОЗУ и ПЗУ приведена на рисунке 15.35.
В данной схеме кольцевой регистр образуется ОЗУ и счетчиком. При поступлении на счетный вход счетчика тактовых импульсов на входы умножителя-накопителя поступают задержанные отсчеты данных и соответствующие им весовые коэффициенты фильтра.
Коэффициенты счета счетчиков Сч1 и Сч2 различаются. Коэффициент счета счетчика Сч2 равен N+1, то есть равен количеству тактовых импульсов, поступающих за один период дискретизации обрабатываемого сигнала. Коэффициент счета счетчика Сч1 равен N. В результате адрес ОЗУ после вычисления очередного выходного значения фильтра сдвигается на одну позицию. Так обеспечивается сдвиг данных в линии задержки фильтра.
Рисунок 14.35 – Структурная схема цифрового фильтра
После поступления на тактовый вход фильтра N+1 импульсов, счетчик Сч1 указывает на самое старое значение данных, записанное в ОЗУ. В этот момент ОЗУ переводится в режим записи, открывается ключ и обнуляется регистр-аккумулятор сигналом, вырабатываемым с выхода дешифратора, подключенного к счетчику Сч2. В результате старое значение данных заменяется на новый отсчет входного сигнала.
Итак, приведенная на рисунке 15.35 схема выполняет те же самые действия, что и прямая реализация фильтра с конечной импульсной характеристикой, но при этом в несколько раз проще. Кроме того, эта схема очень легко перенастраивается на фильтры с различным числом коэффициентов. Для этого достаточно просто изменить коэффициент счета цифровых счетчиков Сч1 и Сч2.
Однородный цифровой фильтр
В предыдущей главе мы научились осуществлять фильтрацию в цифровом виде, однако часто цифровую фильтрацию требуется осуществить на очень высоких частотах дискретизации полезного сигнала. Для увеличения быстродействия желательно уменьшить время выполнения операций каждым из блоков, входящих в состав цифрового фильтра. Наиболее сложным внутренним устройством обладают цифровые умножители, то есть быстродействие фильтра в целом в основном определяется именно этим блоком. Было бы неплохо отказаться от использования умножителей в составе цифрового фильтра.
На очень высоких частотах для подавления мешающих сигналов обычно используется так называемый однородный фильтр [1]. Для реализации этого фильтра не требуются умножители. Однородный фильтр представляет собой фильтр с конечной импульсной характеристикой, обладающий прямоугольной импульсной характеристикой (то есть представляет собой обычный усреднитель).
Передаточная характеристика однородного фильтра описывается формулой:
(15.3)
Для однородного фильтра седьмого порядка эта формула выглядит следующим образом:
(15.4)
Структурная схема фильтра, реализующего формулу 14.3, приведена на рисунке 15.36.
Рисунок 15.36 – Структурная схема однородного фильтра седьмого порядка
Этот фильтр реализует математическую операцию скользящего среднего. Применив к импульсной характеристике фильтра (15.4) дискретное преобразование Фурье, получим выражение, описывающее его амплитудно-частотную характеристику.
(15.5)
Это хорошо известная функция sin(x)/x. График амплитудно-частотной характеристики однородного фильтра приведен на рисунке 15.37. Как и ожидалось, однородный фильтр является фильтром низкой частоты. Так как импульсная характеристика данного фильтра симметрична, то его фазовая характеристика будет строго линейна. Это означает, что однородный фильтр не вносит фазовых искажений в исходный цифровой сигнал. Однако глубина подавления частот вне полосы пропускания у рассмотренного фильтра для большинства приложений явно недостаточна. Известно, что при включении нескольких фильтров друг за другом, глубина подавления мешающих сигналов возрастает, так как при последовательном включении четырехполюсников, их коэффициенты передачи перемножаются.
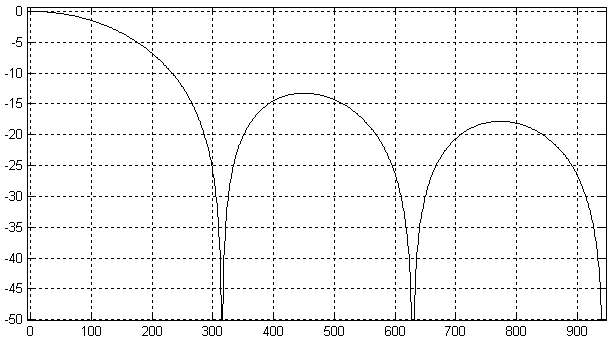
Рисунок 15.37 – Амплитудно-частотная характеристика однородного фильтра
Давайте включим четыре однородных фильтра последовательно друг за другом. На рисунке 15.38 приведены амплитудно-частотные характеристики, полученные для одно- двух- трех- и четырехкаскадного однородного фильтра.
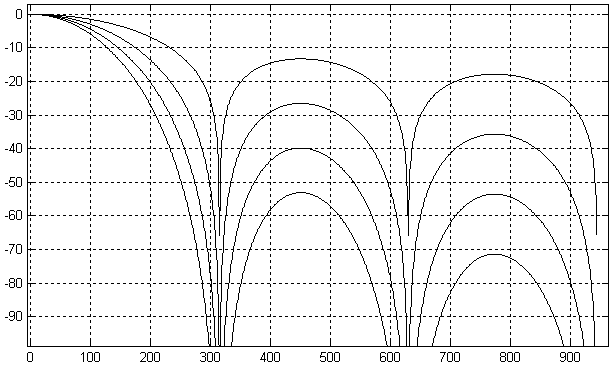
Рисунок 15.38 – Амплитудно-частотная характеристика многокаскадного однородного фильтра
Как видно из этих амплитудно-частотных характеристик, применение многокаскадного однородного фильтра позволяет достичь требуемого подавления мешающих сигналов.
Обычно однородные фильтры используются в составе устройств повышения частоты дискретизации (интерполяции) сигнала или устройств понижения частоты дискретизации (децимации) сигнала. В этом случае можно дополнительно упростить схему однородного фильтра и тем самым увеличить быстродействие схемы, но мы рассмотрим это в последующих главах.
К сожалению, однородный фильтр вносит амплитудные искажения в полосе полезного сигнала, поэтому обычно он используется вместе с дополнительным нерекурсивным фильтром. Этот дополнительный фильтр кроме своей основной задачи должен компенсировать искажения, вносимые в сигнал однородным фильтром.
На этом можно завершить краткий обзор, посвященный реализации фильтров в цифровом виде. Ну а теперь рассмотрим конкретные примеры применения цифровых фильтров для реализации типовых задач, встречающихся в радиотехнических устройствах.