Правило поглощения.
х1 + х 1х2 х3 = х1 (1+ х2 х3) = х1
Одна переменная поглощает другие.
Правило склеивания.
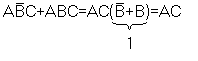
Это правило выполняется только по одной переменной.
Также как в обычной математике, в алгебре логики имеется старшинство операций. При выполнении логических выражений первым выполняется:
Действие в скобках.
Операция с одним операндом (одноместная операция) – "НЕ".
Конъюнкция – "И".
Дизъюнкция – "ИЛИ".
Сумма по модулю два.
Операции одного ранга выполняются слева направо в порядке написания логического выражения. Алгебра логики линейна и для неё справедлив принцип суперпозиции.
6.2 Построение цифровой схемы по произвольной таблице истинности
Любая логическая схема без памяти полностью описывается таблицей истинности. При этом не обязательно чтобы все комбинации входных сигналов были полезными. Возможна ситуация, когда только часть комбинаций входных сигналов является полезной. В этом случае выходные сигналы для оставшихся комбинаций входных сигналов могут быть доопределены произвольно. Обычно при этом стараются выбирать выходные сигналы таким образом, чтобы схема получилась простейшей.
Для реализации логических схем с произвольной таблицей истинности используется сочетание простейших логических элементов "И" "ИЛИ" "НЕ". Существует два способа синтеза схем, реализующих произвольную таблицу истинности. Это СКНФ (логическое произведение суммы входных сигналов) и СДНФ (сумма логических произведений входных сигналов).
При построении схемы, реализующей произвольную таблицу истинности, каждый выход анализируется (и строится схема) отдельно.
В настоящее время наиболее распространены микросхемы, совместимые с ТТЛ технологией, а в этой технологии проще всего получить элементы "И". Поэтому первым рассмотрим способ реализации произвольной таблицы истинности основанный на СДНФ.
Для реализации таблицы истинности при помощи логических элементов "И" достаточно рассмотреть только те строки таблицы истинности, которые содержат логические "1" в выходном сигнале. Строки, содержащие в выходном сигнале логический ноль, в построении схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую единицу, реализуется схемой логического "И" с количеством входов, совпадающим с количеством входных сигналов в таблице истинности.
Входные сигналы, описанные в таблице истинности логической единицей, подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логическим нулем, подаются на вход этой же схемы "И" через инверторы. Объединение сигналов с выходов схем "И", реализующих отдельные строки таблицы истинности, производится при помощи схемы логического "ИЛИ". Количество входов в схеме "ИЛИ" определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая единица.
Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную в таблице 6.1.
Таблица 6.1 – Пример таблицы истинности
Входы |
Выходы |
||||
х0 |
х1 |
х2 |
х3 |
F0 |
F1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
Для построения схемы, реализующей сигнал F0, достаточно рассмотреть строки, выделенные жирным шрифтом. В рассматриваемой таблице истинности имеются всего три строки, содержащие единицу в выходном сигнале F0, поэтому в формуле СДНФ будет содержаться три произведения входных сигналов:
Полученная формула в схеме на рисунке 6.6 реализуются микросхемой D2. Как и в формуле, каждая строка таблицы истинности реализуется своей схемой "И", затем выходы этих схем объединяются схемой "ИЛИ". Количество входов элемента "И" однозначно определяется количеством входных сигналов в таблице истинности. Количество этих элементов, а значит и количество входов в логическом элементе "ИЛИ" определяется количеством строк с единичным сигналом на реализуемом выходе схемы.
Для построения схемы, реализующей сигнал F1, достаточно рассмотреть строки, выделенные курсивом. Эти строки в схеме на рисунке 6.6 реализуются микросхемой D3. Принцип построения этой схемы не отличается от примера, рассмотренного выше. В таблице истинности присутствуют всего три строки, содержащие единицу в выходном сигнале F1, поэтому в формуле СДНФ выхода F1 будет содержаться три произведения входных сигналов:
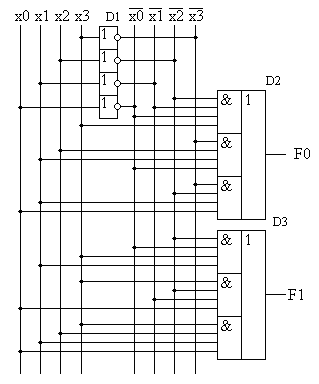
Рисунок 6.6 – Принципиальная схема, реализующая таблицу истинности, приведенную в таблице 6.1
Обычно при построении цифровых схем после реализации таблицы истинности производится минимизация схемы, но в данном случае для упрощения понимания материала минимизация производиться не будет. Это оправдано еще и с той точки зрения, что схемы, построенные по ДНФ, обычно обладают максимальным быстродействием. При реализации схемы на ТТЛ микросхемах быстродействие такого узла будет равно быстродействию одиночного инвертора.
Для иллюстрации этого утверждения рассмотрим схему логического элемента "2И‑2ИЛИ‑НЕ", выполненного по ТТЛ технологии. Она приведена на рисунке 6.7. Основные компоненты, определяющие быстродействие этой схемы – это транзисторы, образующие схему "ИЛИ", так как только они обладают усилением по напряжению, а, значит, их входная ёмкость увеличивается за счёт эффекта Миллера.
Но ведь эти транзисторы соединены параллельно! Это означает, что время задержки сигнала по каждой цепи не суммируются. Быстродействие схемы в целом будет определяться наибольшей из рассматриваемых задержек сигнала, а быстродействие всей схемы в целом будет равно быстродействию одиночного (наихудшего с точки зрения быстродействия) инвертора.
Рисунок 6.7 – Принципиальная схема ТТЛ микросхемы "2И-2ИЛИ-НЕ"
Применение СКНФ для разработки цифровой схемы оправдано при большом количестве единиц в таблице истинности, описывающей выходной сигнал, как, например, в таблице истинности, приведенной в таблице 6.2.
Для реализации таблицы истинности при помощи логических элементов "ИЛИ" достаточно рассмотреть только те строки таблицы истинности, которые содержат логические "0" в выходном сигнале. Строки, содержащие в выходном сигнале логическую единицу, в построении схемы не участвуют. Каждая строка, содержащая в выходном сигнале логический ноль, реализуется логическим элементом "ИЛИ" с количеством входов, совпадающим с количеством входных сигналов в таблице истинности. Входные сигналы, описанные в таблице истинности логическим нулём, подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логической единицей, подаются на вход этой же схемы "ИЛИ" через инверторы.
Таблица 6.2 – Пример таблицы истинности
|
Входы |
Выходы |
||||
№ комбинации |
х0 |
х1 |
х2 |
х3 |
F0 |
F1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
1 |
1 |
3 |
0 |
0 |
1 |
1 |
1 |
1 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
5 |
0 |
1 |
0 |
1 |
1 |
0 |
6 |
0 |
1 |
1 |
0 |
1 |
0 |
7 |
0 |
1 |
1 |
1 |
1 |
1 |
8 |
1 |
0 |
0 |
0 |
1 |
1 |
9 |
1 |
0 |
0 |
1 |
1 |
1 |
Объединение сигналов с выходов логических элементов "ИЛИ", реализующих отдельные строки таблицы истинности, производится при помощи логического элемента "И". Количество входов в логическом элементе "И" определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая единица.
Для построения схемы, реализующей сигнал F0, достаточно рассмотреть строки, выделенные курсивом. В рассматриваемой таблице истинности имеются всего две строки, содержащие логический ноль в выходном сигнале F0, поэтому в формуле СКНФ будет содержаться две суммы входных сигналов:
Полученная формула в схеме, приведённой на рисунке 6.8, реализуются логическим элементом D2.
Для построения схемы, формирующей выходной сигнал F1, достаточно рассмотреть строки, выделенные в таблице 6.2 жирным шрифтом. Эти строки в схеме на рисунке 6.8 реализуются микросхемой D3. Принцип построения этой схемы не отличается от примера, рассмотренного выше. В таблице истинности присутствуют всего две строки, содержащие ноль в выходном сигнале F1, поэтому в формуле СКНФ, записанной для выхода F1, будет содержаться две суммы входных сигналов:
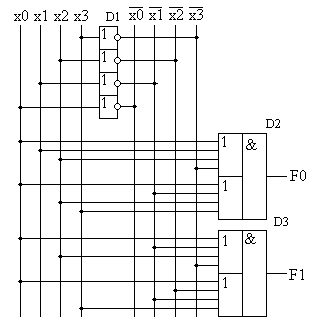
Рисунок 6.8 – Принципиальная схема цифрового устройства с таблицей истинности, приведенной в таблице 6.2
Как видно из приведённых примеров, построение цифровой схемы во многом формализовано и не вызывает каких либо затруднений. В следующих главах будут рассмотрены дополнительные примеры реализации комбинационных цифровых устройств. В качестве примеров послужат наиболее распространённые виды цифровых комбинационных микросхем.