5.2 Преобразование чисел из одной системы счисления в другую
При проектировании цифровых устройств достаточно часто требуется уметь переводить число из одной системы счисления в другую. Давайте научимся выполнять такие действия. Преобразование целых чисел и правильных дробей выполняется по разным правилам. В действительном числе преобразование целой и дробной части производят по отдельности.
Преобразование целой части числа.
Для преобразования целочисленного значения необходимо исходное число разделить на основание новой системы счисления до получения целого остатка, который является младшим разрядом числа в новой системе счисления (единицы). Полученное частное снова делим на основание системы, и так до тех пор, пока частное не станет меньше основания новой системы счисления. Все операции выполняются в исходной системе счисления.
Рассмотрим для примера перевод числа из десятичной системы счисления в двоичную. Возьмём десятичное число А10 = 124 и поделим его на основание двоичной системы, то есть на число 2. Деление будем производить «уголком». В результате первого деления получим разряд единиц (самый младший разряд). В результате второго деления получим разряд двоек. Деление продолжаем, пока результат деления больше двух. В конце операции преобразования получили двоичное число 11111002:
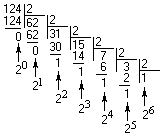
Для того, что бы проверить, нет ли ошибки, преобразуем получившееся двоичное число в десятичную систему по обычной формуле разложения:
126+125+124+123+122+021+020=6410+3210+1610+810+410=124
Теперь то же самое число переведём в восьмеричную систему счисления. Для этого число 12410 будем делить на число 8.
Как видим, остаток от первого деления равен 4. То есть младший разряд восьмеричного числа содержит цифру 4 (единицы). Остаток от второго деления равен 7. то есть второй разряд восьмеричного числа – это цифра 7. Старший разряд получился равным 1. То есть в результате многократного деления мы получили восьмеричное число 1748.
Проверим, не ошиблись ли мы в процессе преобразования? Для этого преобразуем получившееся двоичное число в десятичную систему по обычной формуле разложения:
182+781+480=6410+5610+410=124
А можно ли осуществить перевод из восьмеричной системы счисления в двоичную делением? Можно! Но деление нужно произвести по правилам восьмеричной арифметики. Правила работы в восьмеричной системе счисления мы рассмотрели в предыдущей главе. Рассмотрим пример перевода в двоичную форму полученного ранее восьмеричного числа 1748. Разделим его на основание новой системы счисления 2:
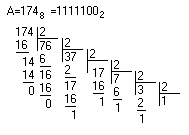
Как мы убедились, выполнять деление в восьмеричной системе очень неудобно, ведь подсознательно мы делим в десятичной системе счисления. Если обратить внимание на то, что число 8 является степенью числа 2, то можно считать восьмеричную систему счисления просто более короткой записью двоичного числа. Это означает, что для представления восьмеричной цифры можно использовать три двоичных бита (8=23). Составим таблицу соответствия для такого преобразования.
Таблица 5.6 – Таблица соответствия восьмеричных цифр
и двоичного кода
-
Двоичный код
Восьмеричная цифра
Десятичный эквивалент
000
0
0
001
1
1
010
2
2
011
3
3
100
4
4
101
5
5
110
6
6
111
7
7
Используя эту таблицу можно просто заменить каждую восьмеричную цифру тремя двоичными битами. Три двоичных бита обычно называют триадой или трибитом. Теперь переведём восьмеричное число 1748 в двоичную форму при помощи таблицы 5.6:
Аналогично можно выполнить перевод числа из двоичной системы в восьмеричную. Для этого двоичное число разбивают на триады относительно крайнего правого разряда (или двоичной запятой) и, используя таблицу 5.6, каждой триаде ставят в соответствие восьмеричную цифру.
Аналогичным образом можно выполнить перевод числа из шестнадцатеричной формы в двоичную и обратно. В этом случае для представления шестнадцатеричной цифры потребуется четыре двоичных разряда. Четыре двоичных разряда обычно называют тетрадой. Иногда при переводе иностранной литературы используется термин нибл.
Составим таблицу соответствия двоичных тетрад и шестнадцатеричных цифр. Для этого будем просто прибавлять единицу к значению предыдущей строки в каждом столбце таблицы, в соответствии с используемой в этом столбце системой счисления. Результат приведён в таблице 5.7.
В качестве примера использования таблицы 5.7 переведем шестнадцатеричное число 7С16 в двоичную форму представления:
Таблица 5.7 – Таблица соответствия шестнадцатеричных цифр
и двоичного кода
-
Двоичный код
Шестнадцатеричная цифра
Десятичный эквивалент
0000
0
0
0001
1
1
0010
2
2
0011
3
3
0100
4
4
0101
5
5
0110
6
6
0111
7
7
1000
8
8
1001
9
9
1010
A
10
1011
B
11
1100
C
12
1101
D
13
1110
E
14
1111
F
15
Пример преобразования двоичного числа в восьмеричную и шестнадцатеричную форму приведён на рисунке 5.1.
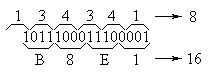
Рисунок 5.1 – Пример преобразования двоичного числа в восьмеричную и шестнадцатеричную форму
На этом рисунке внизу выделены двоичные тетрады и соответствующие им шестнадцатеричные цифры. Их соответствие можно проверить при помощи таблицы 5.7. Сверху выделены триады и соответствующие им восьмеричные цифры. Старшая триада получилась неполной. Для того чтобы можно было бы воспользоваться таблицей 5.6. её необходимо дополнить старшими незначащими нулями
Преобразование дробной части числа.
Так как дробная часть числа меньше единицы, то её преобразование выполняется умножением исходного числа на основание новой системы счисления. Целая часть результата умножения будет старшим разрядом числа в новой системе счисления. Дробную часть произведения снова умножают на основание системы счисления. Операция умножения выполняется до достижения требуемой точности результата. Все операции выполняют по правилам исходной системы счисления.
Для примера рассмотрим перевод дробного числа из десятичной системы счисления в двоичную. Пусть исходное число A будет равно 0,35. Выполним операцию последовательного умножения, как это показано на рисунке 5.2.
Рисунок 5.2 – Пример операции последовательного умножения
В результате описанных действий получим двоичное представление числа A:
A = 0,3510 0,01011=0,34375
В общем случае перевод правильных дробей является приблизительным. Число разрядов в новой системе можно найти исходя из одинаковой точности представления чисел в разных системах счисления. Одинаковая точность числа, записанного в различных системах счисления, достигается при одинаковых весах младших разрядов соответствующей системы счисления. Определить вес младшего разряда числа можно по следующей формуле:
M =q -n,
где q – основание системы счисления.
В предыдущем примере для десятичного числа 0.35 вес младшего разряда M = 1/100 = 0.01. В полученном двоичном числе вес младшего разряда будет равен 1/32 0,03. То есть при операции преобразования числа в двоичную форму мы ухудшили точность представления числа в три раза. Для одинаковой точности представления чисел в различных системах счисления необходимо выполнить равенство:
,
где p и q – основания старой и новой систем счисления соответственно.
Для определения необходимого количества разрядов в новой системе счисления возьмём логарифм по основанию (p) от этого равенства:
,
откуда найдём требуемое количество разрядов:
Определим необходимое число разрядов в двоичной системе счисления для рассмотренного ранее примера:
В использованном нами примере количество разрядов десятичного числа после запятой n10 = 2, то есть в двоичной системе счисления для той же точности числа количество разрядов должно быть равно:
Если же требуется обеспечить точность представления числа до трёх разрядов после запятой n10 = 3, то количество двоичных разрядов должно быть не менее:
Определим формулы пересчёта количества разрядов, требующихся для записи числа в восьмеричной и шестнадцатеричной системе счисления:
,
В рассмотренном выше примере для записи десятичного числа 0,3510 в восьмеричной форме с той же точностью по этой формуле потребуется три разряда. Проверим это утверждение:
Аналогичным образом можно осуществлять перевод в любую систему счисления. Исключением является перевод из двоичной системы счисления в восьмеричную или шестнадцатеричную. Напомним, что эти системы счисления являются краткой записью двоичного числа, поэтому в этом случае можно переводить числа из одной системы счисления в другую при помощи таблиц перехода 5.6 и 5.7. Двоичное число разбивается на триады для перевода в восьмеричную систему счисления или на тетрады для перевода в шестнадцатеричную систему счисления. Разбиение начинается от двоичной запятой.