3. Фундаментальные пределы точности измерений

3.1. Современные представления о макро и микромире.

Эти представления включают накопленный опыт физических явлений и процессов, которые представлены различными теориями, положениями, результатами экспериментов и др. Основное положение молекулярно-кинетической теории строения вещества, вытекающее из опытных фактов, заключается в том, что все макроскопические тела состоят из атомов и молекул, находящихся в состоянии непрерывного хаотического теплового движения. Наиболее убедительным опытным фактом, наглядно подтверждающим хаотический характер теплового движения и зависимость интенсивности этого движения от температуры, является броуновское движение.

Наблюдая в микроскоп за движением взвешенных в жидкости мелких частиц, можно обнаружить, что каждая частица совершает хаотическое движение. Представление о характере блуждания частицы можно получить, если фиксировать ее положение в поле зрения измерительного микроскопа через равные промежутки времени. Соединив последовательные положения частицы прямыми, мы получим ломаную линию, подобную изображенной на рис. 3.1.

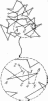
Рис. 3.1 Броуновское движение

Направления соседних участков ломаной линии составляют всевозможные углы друг с другом, так что не удается подметить никакой закономерности в изменении направления ломаной линии. Чем короче промежутки времени, через которые фиксируется положение частицы, тем более изломанной будет выглядеть «траектория» частицы: точки А, В, С, ... фиксируют положение частицы через 30 секунд, а точки 1, 2, 3, ..., соединенные пунктиром, фиксируют ее положение через каждые 5 секунд.

Если наблюдать за движением сразу нескольких взвешенных в жидкости частиц, то можно заметить, что они движутся то в одну сторону, то в противоположные, то под углом друг к другу. Отсюда можно сделать вывод, что наблюдаемое броуновское движение не связано с перемещением потоков жидкости, так как в этом случае соседние частицы всегда перемещались бы вместе. На опыте же никакой согласованности в движении соседних частиц не наблюдается, движутся они совершенно независимо друг от друга.

Изменяя температуру, при которой производится опыт, можно заметить, что с увеличением температуры интенсивность броуновского движения растет, с понижением температуры оно замирает.

Такой характер движения позволяет предположить, что броуновская частица движется под действием ударов, получаемых от молекул жидкости, в которой она находится.

Броуновское движение не только принесло неопровержимое доказательство реальности атомов и молекул, но и позволило впервые подсчитать количество молекул в макроскопическом объеме вещества, т. е. определить значение постоянной Авогадро: N_A = 6,022·10²³ моль^-1.

Таким образом, было окончательно установлено, что тепловая форма движения материи обусловлена хаотическим движением атомов или молекул, из которых состоят макроскопические тела.

Исторически при изучении макроскопических свойств физических систем независимо сложились два различных подхода — статистический и термодинамический.

Статистический подход, или статистическая механика устанавливает связь между экспериментально измеряемыми макроскопическими величинами, характеризующими систему в целом, такими, как давление, объем, температура, напряженность электрического поля и т. д., и микроскопическими характеристиками системы, такими, как массы и заряды составляющих систему частиц, их координаты и импульсы и т. д.

Определение состояния системы в статистической механике является гораздо менее детализированным, чем в механике, так как опирается лишь на небольшое число макроскопических параметров, измеряемых на опыте. В большинстве случаев такое сокращенное описание системы является вполне достаточным, ибо нас, как правило, совершенно не интересует детальная информация о движении отдельных молекул.

Но значения макроскопических параметров, разумеется, зависят от движения молекул, и задача статистической механики — выразить свойства системы в целом через характеристики отдельных молекул, т. е, перекинуть мост между макро- и микроскопическими описаниями системы. При этом требуется установить связь макроскопических параметров системы со средними значениями микроскопических величин и дать способ вычисления этих средних значений на основе законов движения отдельных молекул.

Тепловое равновесие — это всегда динамическое равновесие. Тепловое движение атомов или молекул, из которых состоит макроскопическая система, никогда не прекращается.

Поэтому макроскопические величины, характеризующие систему в целом, строго говоря, никогда не остаются постоянными, а испытывают малые беспорядочные колебания вблизи некоторых средних значений. Такие хаотические отклонения от средних значений тех или иных величин, происходящие в течение малых промежутков времени, называются флуктуациями. Относительная величина флуктуации тем больше, чем меньше размеры изучаемой системы.

Яркий пример флуктуации — это дрожание зеркальца чувствительного гальванометра.

Гальванометр − электроизмерительный прибор высокой чувствительности для измерения малых токов и напряжений.

Макроскопическая система, состоящая из подвижной катушки гальванометра, подвешенной на упругой кварцевой нити, в состоянии механического равновесия была бы совершенно неподвижной, если бы не тепловое движение.

Удары молекул воздуха, совершающих тепловое движение, приводят к тому, что угол поворота зеркальца испытывает хаотические колебания вблизи положения механического равновесия.

Фактически это то же броуновское движение, которое отличается от рассмотренного движения взвешенной в жидкости частицы только тем, что здесь рассматривается не поступательное, а вращательное движение вблизи устойчивого, а не безразличного положения равновесия. Интенсивность такого движения зависит от температуры, оно принципиально неустранимо и ставит предел чувствительности измерительной аппаратуры.

Если полное число молекул в изучаемой системе велико, то флуктуации макроскопических параметров почти никогда не возникают. Если число частиц в системе очень велико, то относительная величина флуктуации любого параметра очень мала по сравнению со средним значением этого параметра, и ею почти всегда можно пренебречь. Поэтому мы обычно не осознаем факта существования флуктуации, когда имеем дело с большими макроскопическими системами. Но если система достаточно мала, то флуктуации могут быть легко обнаружены и часто имеют большое значение.

Тепловые флуктуации ставят предел чувствительности любых измерительных приборов. При измерении малых значений физических величин или слабых сигналов флуктуации в чувствительном элементе измерительного прибора могут оказаться сравнимыми с измеряемой величиной.

Флуктуации, возникающие в самом измерительном приборе, затрудняют измерения и поэтому называются шумами.

Процесс является необратимым, если обратный процесс в действительности почти никогда не происходит.

Строгого запрещения для такого процесса нет — он просто слишком маловероятен, чтобы его можно было наблюдать на опыте.

С точки зрения представлений молекулярно-кинетической теории второй закон термодинамики утверждает то, что в природе в макроскопических системах процессы развиваются в таком направлении, когда менее вероятные состояния системы заменяются на более вероятные. Такая интерпретация второго закона термодинамики была впервые предложена Больцманом. При рассмотрении флуктуации плотности идеального газа было выяснено, что состояния газа, при которых распределение молекул близко к равномерному, встречаются гораздо чаще, чем далекие от равновесия состояния с сильно неравномерным распределением молекул. Другими словами, состояния с неравномерным распределением молекул по объему, при которых число молекул в правой и левой половине сосуда сильно различается, имеют гораздо, меньшую вероятность, чем состояния с почти равномерным распределением, близкие к равновесному. Итак, необратимый процесс приближения к равновесию — это переход к наиболее вероятному макроскопическому состоянию.

Необратимый характер процессов перехода в состояние теплового равновесия справедлив только для больших макроскопических систем. С термодинамической точки зрения изолированная система, пришедшая в состояние теплового равновесия, не может самопроизвольно выйти из этого состояния. Однако статистическая механика допускает существование флуктуации, которые фактически представляют собой самопроизвольные отклонения системы от равновесия. Как уже отмечалось, чем больше частиц в системе, тем меньше относительная величина флуктуации любого макроскопического параметра, и для достаточно большой системы флуктуациями вообще можно пренебречь.

Именно поэтому для таких систем справедлив второй закон термодинамики.

В системах с небольшим числом частиц относительная величина флуктуации велика, т. е. самопроизвольные отклонения какой-либо величины от ее среднего значения могут быть сравнимы с самим средним значением. Такая система часто самопроизвольно выходит из состояния равновесия, и второй закон термодинамики здесь неприменим. Характерный пример нарушения второго закона термодинамики в достаточно малых системах — броуновское движение, при котором взвешенная в жидкости частица получает кинетическую энергию от молекул окружающей среды, хотя температура среды не выше, чем температура самой броуновской частицы.

Дробовой эффект — небольшие флуктуации величины электрического тока от среднего значения, вызванные неравномерностью диффузии носителей тока в полупроводниках или неравномерностью эмиссии электронов с катода в электровакуумных приборах.

Диффузия − процесс проникновения атомов одного вещества между атомами (молекулами) другого вследствие теплового движения.

Эмиссия − испускание электронов нагретыми телами в вакуум или окружающую среду. Широко применяется в электровакуумных приборах.

При протекании тока в полупроводниках, носители заряда испытывают большое число столкновений с атомами и другими носителями внутри катода, в результате чего величина и направление скорости отдельного носителя при пролете через какое-либо сечение полупроводника могут быть различными. Это приводит к тому, что число носителей, прошедших через сечение за одинаковые малые промежутки времени, оказывается различным, вследствие чего ток испытывает случайные отклонения от своего среднего значения (флуктуации).

Термин «дробовой эффект» (дробовой шум) возник в связи с тем, что благодаря ему в громкоговорителе, подключенном к выходу усилителя или радиоприёмника, появляется акустический шум, напоминающий шум сыплющихся дробинок.

Фликкер-эффект (от англ. flicker – мерцание), эффект мерцания катода, медленные флуктуации электрических токов и напряжений в электровакуумных и газонаполненных электронных приборах, обусловленные испарением атомов вещества катода; диффузией их из глубинных слоев катода к его поверхности; бомбардировкой катода положительными ионами, приводящей к ионному внедрению и образованию слоев посторонних атомов на поверхности катода; структурными изменениями катода. Пространственный заряд частично подавляет фликкер-эффект.

Ионное внедрение − введение посторонних атомов внутрь твёрдого тела путём бомбардировки его поверхности ионами. Средняя глубина проникновения ионов в мишень тем больше, чем больше энергия ионов.

Пространственный заряд − электрический заряд, рассредоточенный по некоторому объёму.

Макромир и микромир − две специфические области объективной реальности, различающиеся уровнем структурной организации материи. Сфера макроявления − это обычный мир, в котором живет и действует человек (планеты, земные тела, кристаллы, большие молекулы и др.). Качественно иную область представляет микромир (атомы, ядра, элементарные частицы и др.), где размеры объектов меньше миллиардных долей сантиметра, а временные промежутки порядка миллиардных долей секунды, т. е. непосредственно недоступны наблюдению. Каждый из этих миров характеризуется своеобразием строения материи, пространственно-временных и причинных отношений, закономерностей движения. Так, в макромире материальные объекты имеют резко выраженную прерывную, корпускулярную или непрерывную, волновую природу и их движение подчиняется динамическим законам классической механики. Для явлений микромира, напротив, характерна тесная связь корпускулярных и волновых свойств, которая находит свое выражение в статистических законах квантовой механики.

Своеобразная граница раздела макро- и микромира была установлена в связи с открытием постоянной Планка.

Существенным аспектом этой новой константы явилась «конечность взаимодействия», означавшая, что любые взаимодействия между объектами в микромире (в том числе между прибором и микрочастицей) не могут быть меньше значения кванта действия.

Специфика макро- и микромира находит свое отражение в познании, приводит к ограничению сферы применимости старых физических теорий и возникновению новых (теория относительности, квантовая механика, физика элементарных частиц).

Наука показывает тесную связь между макро- и микромиром и обнаруживает, в частности, возможности появления макроскопических объектов при столкновении микрочастиц высокой энергии.

По первоначальному смыслу понятие "элементарный" означает простейший, не имеющий внутренней структуры, неделимый. По мере углубления наших знаний о природе материи многие объекты микромира, ранее считавшиеся элементарными, потеряли право так называться.

Известным примером такого рода является атом (по-гречески "неделимый"). Атомы, отвечающие определенным химическим элементам, как известно, состоят из электронов и атомных ядер.

Физические исследования показали, что ядра тоже составные частицы, они построены из протонов и нейтронов.

Следовательно, ни ядра, ни тем более атомы не являются элементарными частицами. Электроны, а также протоны и нейтроны называются элементарными частицами, хотя протоны и нейтроны, как установлено, состоят из кварков.

Элементарная частица — собирательный термин, относящийся к микрообъектам в субъядерном масштабе, которые невозможно расщепить на составные части. Их строение и поведение изучается физикой элементарных частиц. Понятие элементарных частиц основывается на факте дискретного строения вещества. Ряд элементарных частиц имеет сложную внутреннюю структуру, однако разделить их на части невозможно.

Другие элементарные частицы являются бесструктурными и могут считаться первичными фундаментальными частицами.

Начиная с 1932 года, было открыто более 400 элементарных частиц. Первой открытой элементарной частицей был электрон. Его открыл английский физик Томсон в 1897 году.

Первой открытой античастицей был позитрон − частица с массой электрона, но положительным электрическим зарядом. Это античастица была обнаружена в составе космических лучей американским физиком Андерсоном в 1932 году.

Важнейшей квантово-механической характеристикой элементарной частицы является спин.

Спин − это собственный момент импульса частицы.

Его значение определяется по тому, какой статистике (Ферми-Дирака или Бозе-Эйнштейна) подчиняется частица.

Спин измеряется в единицах постоянной Планка (h=1,054 ·10⁻³⁴Дж·с) и принимает либо целые, либо полу целые значения.

Статистика Бозе-Эйнштейна − метод описания свойств макроскопической системы, содержащей большое количество частиц с целочисленным спином, взаимодействующим по принципам квантовой механики.

Статистика Ферми-Дирака − метод описания свойств макроскопической системы, содержащей большое количество частиц с полуцелым спином.

Такие частицы подчиняются принципу Паули, согласно которому в любом состоянии, описываемом набором квантовых чисел, может находиться только одна частица.

По величине спина все элементарные частицы делятся на два класса:

1. фермионы — частицы с полуцелым спином (например, электрон, протон, нейтрон, нейтрино);

2. бозоны — частицы с целым спином (например, фотон).

По видам взаимодействий элементарные частицы делятся на группы.

Первая группа:

адроны — частицы, участвующие во всех видах фундаментальных взаимодействий. Они состоят из кварков и подразделяются, в свою очередь, на:

− мезоны (адроны с целым спином, т. е. бозоны);

− барионы (адроны с полу целым спином, т. е. фермионы).

К ним, в частности, относятся частицы, составляющие ядро атома — протон и нейтрон.

Вторая группа:

- лептоны — фермионы, которые имеют вид точечных частиц (т. е. не состоящих ни из чего) вплоть до масштабов порядка 10⁻¹⁸м. Не участвуют в сильных взаимодействиях. Участие в электромагнитных взаимодействиях экспериментально наблюдалось только для заряженных лептонов (электроны, мюоны, тау-лептоны) и не наблюдалось для нейтрино. Известны 6 типов лептонов.

Третья группа:

- кварки — дробнозаряженные частицы, входящие в состав адронов. В свободном состоянии не наблюдались. Как и лептоны, делятся на 6 типов и являются бесструктурными, однако, в отличие от лептонов, участвуют в сильном взаимодействии.

Четвертая группа:

- калибровочные бозоны — частицы, посредством обмена которыми осуществляются взаимодействия:

− фотон — частица, переносящая электромагнитное взаимодействие;

− восемь глюонов — частиц, переносящих сильное взаимодействие;

− три промежуточных векторных бозона W⁺, W⁻ и Z⁰, переносящие слабое взаимодействие;

− гравитон — частица, переносящая гравитационное взаимодействие. Существование гравитонов, хотя пока не доказано экспериментально в связи со слабостью гравитационного взаимодействия, считается вполне вероятным.

Адроны и лептоны образуют вещество.

Калибровочные бозоны — это кванты разных видов излучения. Кроме того, в Стандартной Модели с необходимостью присутствует хиггсовский бозон, который, впрочем, пока ещё не обнаружен экспериментально.

Микроскопические массы и размеры элементарных частиц обусловливают квантовую специфику их поведения: квантовые закономерности являются определяющими в поведении элементарных частиц.

Наиболее важное квантовое свойство всех элементарных частиц − это способность рождаться и уничтожаться (испускаться и поглощаться) при взаимодействии с другими частицами. Все процессы с элементарными частицами протекают через последовательность актов их поглощения и испускания.

Различные процессы с элементарными частицами заметно отличаются по интенсивности протекания.

В соответствии с различной интенсивностью протекания взаимодействия элементарных частиц феноменологически делят на 4 класса:

1. Сильное,

2. Электромагнитное,

3. Слабое,

4. Гравитационное.

Сильное взаимодействие элементарных частиц вызывает процессы, протекающие с наибольшей по сравнению с другими процессами интенсивностью и приводит к самой сильной связи элементарных частиц. Именно оно обусловливает связь протонов и нейтронов в ядрах атомов.

Электромагнитное взаимодействие отличается от других участием электромагнитного поля. Электромагнитное поле (в квантовой физике − фотон) либо излучается, либо поглощается при взаимодействии, либо переносит взаимодействие между телами.

Электромагнитное взаимодействие обеспечивает связь ядер и электронов в атомах и молекулах вещества, и тем самым определяет (на основе законов квантовой механики) возможность устойчивого состояния таких микросистем.

Слабое взаимодействие элементарных частиц вызывает очень медленно протекающие процессы с элементарными частицами, в том числе распады квазистабильных частиц. Слабое взаимодействие гораздо слабее не только сильного, но и электромагнитного взаимодействия, но гораздо сильнее гравитационного.Гравитационное взаимодействие элементарных частиц является наиболее слабым из всех известных.

Такое взаимодействие на характерных для элементарных частиц расстояниях дает чрезвычайно малые эффекты из-за малости масс элементарных частиц.

Слабое взаимодействие гораздо сильнее гравитационного, но в повседневной жизни роль гравитационного взаимодействия гораздо заметнее роли слабого взаимодействия. Это происходит потому, что гравитационное взаимодействие (как, впрочем, и электромагнитное) имеет бесконечно большой радиус действия. Поэтому, например, на тела, находящиеся на поверхности Земли, действует гравитационное притяжение со стороны всех атомов, из которых состоит Земля. Слабое же взаимодействие обладает настолько малым радиусом действия, что он до сих пор не измерен.

Теорию, которая призвана объединить электрослабое взаимодействие и великое объединение, называют суперобъединением (или иногда - теорией всего сущего). Она должна охватить все четыре взаимодействия одновременно.

Физики считают, что эту теорию можно создать на основе теории струн. Эта новая теория основана на введении протяженных микрообъектов, которые назвали струнами, они представляют собой пространственно одномерные отрезки с размером планковской длины 10⁻³³ см. Она возникла в результате объединения квантовой теории с общей теорией относительности. Здесь струна заменяет частицу или, в общем случае, любой локализованный в пространстве микрообъект. В этой теории предполагается, что все элементарные частицы, которые известны сегодня или будут открыты в будущем, являются определенными возбужденными состояниями струны.

Понятие струны исключает точечные представления микрообъектов из структуры микромира и сводит физику к геометрии сложных пространств. Тем самым пространство становится самым фундаментальным понятием в физике.

Теория суперструн связана с концепцией суперсимметрии, открытой в 1960-1970-х гг., которая связала между собой фермионы и бозоны. Преобразования суперсимметрии переводят их друг в друга, а также связывают физику с геометрией.

Согласно этой теории объектом современной физики является квантованное суперструнное поле, возбуждением которого выступают суперструны, взаимодействующие между собой и с вакуумом. Струны, в свою очередь, порождают известные нам элементарные частицы.

Кроме того, эта теория приводит к целому ряду очень даже нетривиальных следствий.

Например, предсказывает существование частиц, движущихся со сверхсветовыми скоростями, которые называют тахионами. Более того, как следствие теории возникает представление о так называемом "еренийтеневом" мире, которое, вероятно, может стать объяснением открытого астрономами факта, что скопления галактик и галактики содержат большую массу невидимого "скрытого" вещества, в десятки раз превосходящую массу самих галактик. Итак, в познании строения вещества физика прошла три этапа.

На первом этапе рассматривалось строение атомов и молекул, была исследована их электронная оболочка и т. д.

На втором этапе исследовалось строение атомного ядра как объекта, состоящего из протонов и нейтронов.

На третьем этапе изучается структура самих нуклонов или кварковая структура адронов. Если объект обладает внутренней структурой, он будет характеризоваться и внутренней динамикой, и внутренними движениями. Согласно квантовой механике энергия таких движений квантуется, образуя дискретный спектр.

На разных уровнях познания эти спектры отличаются в основном масштабом энергии.

3.2. Потенциальные ресурсы стабильности параметров физических объектов микромира.

Стабильность есть основная характеристика физических объектов, сред, полей, структур, материалов, материальных и технических объектов.

Это понятие часто используют для объектов (устройств), осуществляющих (генерирующих) те или иные процессы, в том числе производственные (стабильное производство, стабильная торговля и т. д.).

Потенциальные ресурсы стабильности параметров физических объектов микромира следует рассматривать с учетом теоретических тонкостей микромира.

Ресурсы стабильности физических объектов заложены в фундаментальном принципе вещества, который основан на взаимных воздействии составных элементов их строения вещества. Он касается воздействий между элементами в том смысле, что определяет характер взаимных ускорений, а взаимное прибавление ускорений равносильно со взаимным воздействием. Он касается строения вещества в том смысле, что определяет условия, которые связаны с ускорениями и определяет то, что из составных элементов могут возникать стабильные вещественные структуры.

В фундаментальном принципе вещества вмещаются законы динамики Ньютона, законы небесной механики Кеплера, закон свободного падения тел в гравитационном поле Галилея, закон

сохранения энергии и др.

Если существует некая вещь, то можно утверждать, или она должна иметь какие-то составные элементы, или сама должна быть элементом более сложной вещи. Вещество состоит из атомов, атомы состоят из нейтронов, протонов и электронов. Эти элементы могут состоять из гипотетических фундаментальных элементов вещества, которые, структурно соединяясь друг с другом в разновидные конфигурации, в результате дают именно такие более сложные структуры.

Фундаментальный принцип воздействий в веществе есть один, но воздействия, существующие между разновидными сложными структурами, проявляют себя различными способами.

По другому воздействуют друг с другом атомы, когда создают структуру кристаллов, по другому воздействую друг с другом макроструктуры. Главное, необходимо приспособить масштаб, в котором происходит данное явление. Например, стабильное расположение атома в структуре можно рассматривать как суммарное действие ускорений, причиняемых ему всеми другими атомами, а в самой большой степени ускорений, причиняемых ему соседними, самыми близкими атомами.

Фундаментальный принцип вещества в сущности является принципом, который определяет суть и форму элемента как той вещи, которая воздействует на другие элементы.

Поэтому с элементом вещества можно отождествлять пространственное поле. Это поле (или материальная частица) определяется значениями ускорений, которые получают в объеме (либо в пространстве) его воздействия другие подобные пространственные поля.

Такое пространственное поле имеет центрально-симметричный характер, ибо, считая от его центральной точки, ускорения определяют его одинаковым образом в любом направлении. При изменении расстояния от центральной точки изменяются ускорения, а изменения есть в каждом направлении, т. е. они описываются той же математической функцией ускорения.

Результаты исследований показывают на то, что ускорение фундаментальных частиц протекает приблизительно. При больших расстояниях ускорение изменяется обратно пропорционально квадрату расстояния между центральными точками ускоряемого и ускоряющего полей, а также, изменяется пропорционально инертному параметру (коэффициент пропорциональности), который существует в функции ускоряющего поля.

Такую функцию можно называть функцией гравитационного ускорения. При меньших расстояниях изменение ускоряющей функции происходит по-другому.

В области гравитационного ускорения везде существуют ускорения с не нулевыми значениями, а в потенциальной оболочке, при некотором значении расстояния от атома, существуют нулевые значения ускорения. Вблизи такого места, в точках более отдаленных от центра атома (чем точка с нулевым ускорением) существует отрицательное ускорение, которое означает, что при том расстоянии другие атомы ускоряются в направлении «к центру» данного атома, а в точках более близких от центра атома существует положительное ускорение, которое означает, что при том расстоянии другие атомы ускоряются в направлении «от центра» данного атома.

Атом, который в таком месте ускоряется, находится в состоянии прочного равновесия и ведет себя так, как бы он колебался вокруг точки с нулевым ускорением.

Существование и функционирование таких потенциальных оболочек вокруг каждого атома в результате дает эффект динамической стабильности относительного расположения атомов в пространстве.

Результаты исследований атомных структур в виде кристаллов указывают на существование разновидного строения кристаллических структур и на существование в этих структурах разных расстояний между атомами. Эти расстояния между атомами в разных структурах существуют в присутствии в них атомов одного химического элемента среди атомов других химических элементов. Такие расположения атомов друг относительно друга указывает на то, что в атомах существует несколько потенциальных оболочек с разными радиусами, которые концентрически окружают атом. Значит и составные элементы атомов имеют различное количество и различные радиусы потенциальных оболочек.

Определенное взаимодействие такого положения позволяет предположить существование стабильного состояния вещества, а значит и стабильных его размеров.

Другое дело, когда на вещество воздействуют внешние раздражители в виде тепловых, электромагнитных, радиационных и других воздействий. В этом случае, происходит изменение физико-механических свойств, геометрических размеров. Но стоит стабилизировать процесс внешнего воздействия, т. е. привести его к постоянству, как стабилизируются изменившиеся функции и свойства вещества.

В таком состоянии можно проводить измерения параметров, и они будут стабильны.

Таким образом, можно говорить о том, что одним из принципов стабильности параметров объектов микромира является фундаментальный принцип вещества.

3.3. Физико-техническое обеспечение стабильности объектов.

Такое обеспечение подразумевает под собой во-первых, физическое обоснование стабильности объектов и выполняемые ими функции, а во-вторых, техническое обеспечение физических возможностей по обеспечению стабильности объектов. Физическое обеспечение можно рассмотреть на примере математических моделей реальных физических явлений.

Математические модели реальных физических явлений и объектов описывают их с той или иной степенью точности и состоятельны, соответствуют реальности, в некоторой области параметров модели. Динамические объекты это физические или технические объекты, способные воспринимать изменяющиеся внешние воздействия и реагировать на эти воздействия изменением некоторых величин, характеризующих объект. Динамические объекты проявляют в процессе реакции на внешние воздействия свои инерционно-колебательные свойства и неустойчивость (устойчивость).

Математические модели динамических объектов, описывающие начало развития в объекте неустойчивого процесса, вполне можно ограничить классом линейных систем, поскольку на начальном этапе изменение переменных, характеризующих объект, относительно мало.

Как отмечалось выше, причиной потенциальной неустойчивости объекта или системы является наличие в них внутренних обратных связей и достаточная мощность источников энергии.

Рассмотрим описание объекта и объекта, охваченного отрицательной обратной связью (рис. 3.2). По передаточной функции разомкнутого контура легко получить передаточную функцию замкнутого контура с отрицательной обратной связью (ООС).

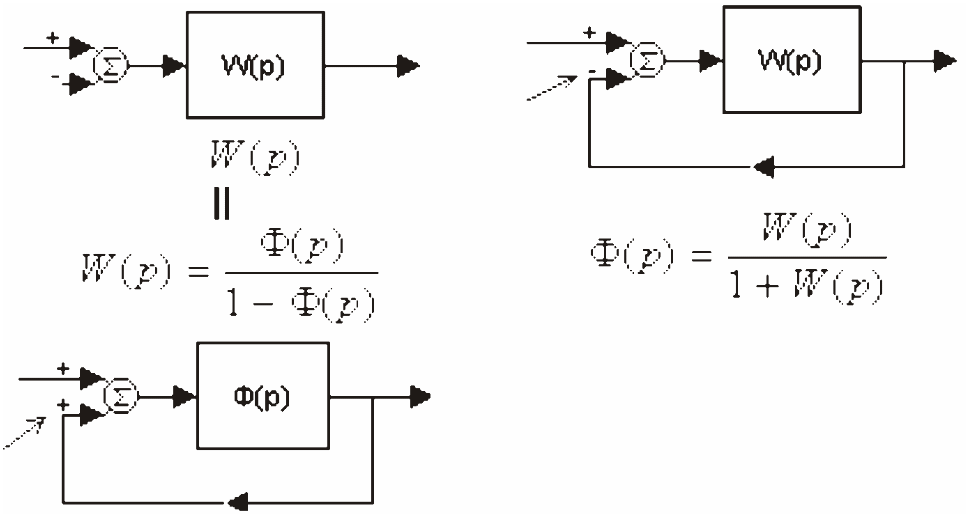
W(p) = 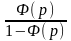Ф (р) =

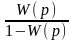
Рис. 3. 2. Схема описания объекта и объекта, охваченного отрицательной обратной связью

Но и наоборот, по передаточной функции замкнутого контура можно получить передаточную функцию разомкнутого контура, формально «разомкнуть» контур, даже если структура некоторого объекта или системы не известна. Отметим, что если исходная линейная модель охватывается отрицательной обратной связью, то для того, чтобы ее «разомкнуть», нужно охватить замкнутую модель положительной обратной связью

Физический смысл обратимости процедуры охвата звеньев обратными связями довольно прост (рис. 3. 3):

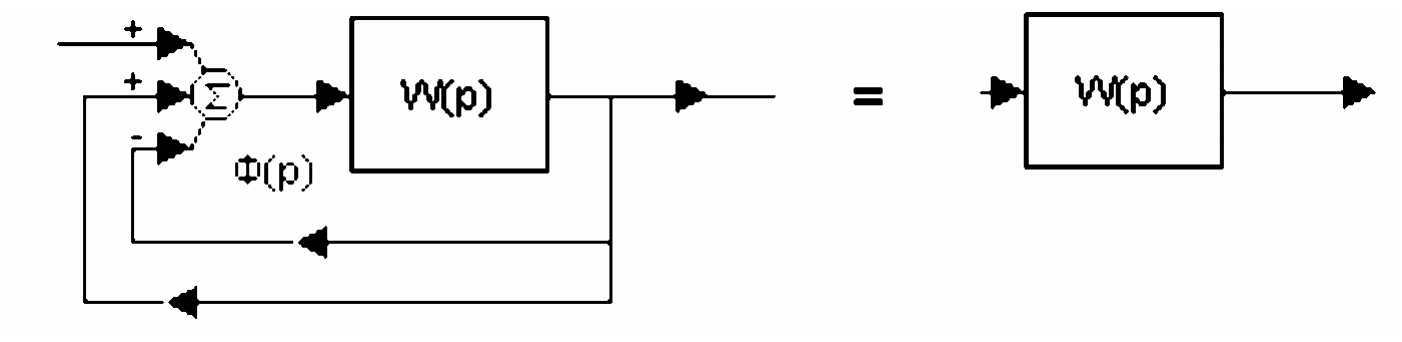
Рис.. 3. 3. Параллельные положительная и отрицательная обратные связи взаимно компенсируют друг друга

Отметим особо, что даже если реальная функциональная или структурная схемы некоторого объекта не известны, а задана только его передаточная функция, то можно формально «разомкнуть» такой объект, представить его в виде контура с ООС, не зависимо от того, есть ли на самом деле контуры в реальном объекте.

Полученная «разомкнутая» модель, соответствуя свойствам моделируемого объекта, не обязательно будет повторять структуру реального объекта, скорее наоборот, поскольку для конкретный объект может быть промоделирован разными, но эквивалентными структурными схемами.

Набор фундаментальных элементарных звеньев, из которых может быть построена линейная модель любого динамического объекта или системы состоит всего из четырех устойчивых звеньев:

- пропорционального, моделирующего усилители и другие без инерционные преобразователи;

- сумматора, обеспечивающего без инерционную реализацию принципа суперпозиции,

- интегратора, моделирующего инерцию, инерционность объектов, а также

- звена запаздывания, моделирующего протяженность объектов и систем в пространстве путем задания времени распространения воздействий от одного элемента к другому.

Контур, построенный из таких элементов, может быть потенциально неустойчивым.

О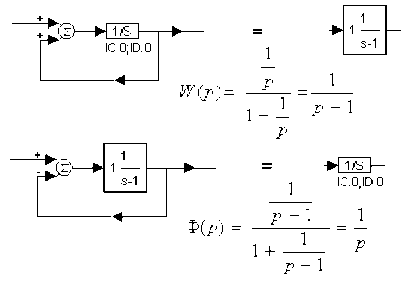 братимся к одному из двух фундаментальны звеньев, определяющих посредством инерционности и запаздывания инерционно-колебательные свойства объекта и его неустойчивость (устойчивость), к интегратору. Если «разомкнуть» интегратор, аналитически или структурно, охватив его положительной обратной связью, то получится неустойчивое звено первого порядка (рис. 3.4): Подобная схема дает неустойчивое звено первого порядка. И наоборот, охват неустойчивого звена первого порядка отрицательной обратной связью дает интегратор. Вот тут и возникает вопрос: неужели в основе интегратора, фундаментального звена любой линейной модели физического или технического объекта лежит неустойчивость, «сдерживаемая» отрицательной обратной связью? Насколько такая математическая модель состоятельна, соответствует реальности, и почему? И если нет, то почему?

Рис. 3.4. Схема «размыкания интегратора”

Отметим, что и неустойчивое звено первого порядка можно также разомкнуть:

W₂(p) = 1/p-2; W₃(p) = 1/p-3; W_n(p) = 1/p-n;

Как видно, рассматриваемая модель интегратора представляет собой матрешку из неограниченного числа контуров. И чем глубже внутрь, тем больше положительный корень характеристического полинома разомкнутого контура, тем выше быстродействие.

Отметим также, что, как показано выше, изменение коэффициента контура, включающего усилитель (П-регулятор) и типовое неустойчивое звено первого порядка, от нуля до бесконечности изменяет свойства замкнутого контура с неустойчивого состояния, через интегратор к устойчивому, близкому по свойствам апериодическому звену.

Как же на самом деле устроен наш мир? Балансирует ли он, опираясь на внутреннюю структурную неустойчивость составляющих его объектов, компенсируемую достаточно сильными отрицательными обратными связями? Или это всего лишь математическая игра ума, выводящая модель физического объекта из области ее состоятельности? Но ведь линейная модель объекта описывается дифференциальными уравнениями, вытекающими из физических законов.

Техническое обеспечение стабильности объекта предполагает в первую очередь техническую диагностику.

Техническая диагностика – это определенный метод, с помощью которого изучают тот или иной объект для определенных целей. Слово «диагностика» произошло от греческого слова «диагнозис», в переводе означает распознание, определение.

Объектом диагностики называется технический объект, состояние которого исследуется, завершающей стадией исследования является получение диагноза, т. е. заключения о состоянии объекта:

1. Исправлен;

2. Не исправен;

3. В объекте имеется какая-то неисправность.

Неисправность в работе агрегата, узла или системы в целом является следствием возникновения дефектов в его элементах.

Дефектами деталей и других элементов машин называется отклонение их от первоначального установленного качества, заданного техническими условиями, т. е. от формы, заданных размеров, показателей физико-механических свойств, качества смазки, чистоты поверхности, окраски и т. д.

Возникновение и развитие дефектов зависит от: несовершенства конструкции, технологии изготовления; условий эксплуатации технического объекта и т. д.

Развитие и появление дефектов вследствие неисправностей долгое время почти не отражается на работе объекта.

Процесс медленного ухудшения показателей считается нормальным и естественным, но при некоторых условиях дефекты возникают и различаются очень быстро.

Количественные показатели за время достигают предельных значений, и объект резко ухудшает свои параметры, а иной раз становится и не пригоден к использованию.

Основой технической диагностики является анализ различных физических процессов, происходящих в работающей машине, и их влияние на ее эксплуатационные показатели, последние в момент времени определяются уровнем и стабильностью характеристик рабочего процесса, качеством деталей и сопряжений, обладающих определенными физическими свойствами, например:

- взаимным расположением; формой, шероховатостью; волнистостью поверхности;

- геометрическими параметрами;

- линейными размерами.

Можно выделить этапы производства и эксплуатации технического объекта, когда его применяли по назначению, подвергали профилактическим проверкам после ремонта и до ремонта.

Для объекта на каждом этапе существования в соответствии со служебным значением задаются определенные эксплуатационные показатели, которым он должен соответствовать, однако вследствие неисправностей это соответствие может нарушаться.

Эксплуатационные показатели охватывают основные параметры объекта, характеризующие выполнение заданных функций, и второстепенные, такие как удобство эксплуатации, внешний вид.

Объект исправен, если он полностью соответствует всем эксплуатационным показателям, все его параметры, как основные, так и второстепенные, находятся в заданных пределах.

Объект работоспособен, если его основные параметры находятся в пределах заданной нормы.

Объект исправно функционирует, если его главные параметры, характеризующие работу в данном режиме и в данное время, не выходят за допустимые пределы.

Неисправность – это выход любого параметра за пределы нормы.

3.4. Пределы точности измерения физических величин.

Процесс измерения сопровождается ошибками, которые вызываются несовершенством измерительных средств, нестабильностью условий проведения измерений, несовершенством самого метода и методики измерений, недостаточным опытом и несовершенством органов чувств человека, выполняющего измерения, а также другими факторами.

Одной из характеристик (мерой) точности измерения является погрешность измерений, как оценка отклонения измеренного значения физической величины от ее истинного значения. Погрешность измерения, выраженная в единицах измеряемой величины, называется абсолютной. Она не всегда является информативной. Например, абсолютная погрешность 0,01 мм может быть достаточно большой при измерениях величин в десятые доли миллиметра и малой при измерениях величин, размеры которых превышают несколько метров. Более информативной величиной является относительная погрешность, под которой понимают отношение абсолютной погрешности измерения к ее истинному значению (или математическому ожиданию). Именно относительная погрешность используется для характеристики точности измерения.

Классификация погрешностей.

Погрешности классифицируются по:

- форме представления (абсолютная, относительная, приведенная);

- причине возникновения (инструментальные, методические, субъективные);

- характеру проявления (систематические, случайные, прогрессирующие, грубые);

- способу измерения (погрешности прямых и косвенных

измерений).

По своему характеру (закономерностям проявления) погрешности измерения подразделяются на систематические, случайные и грубые промахи.

Систематические погрешности.

Систематические погрешности остаются постоянными или изменяются по какому-либо закону при повторных измерениях.

К причинам, вызывающим систематические погрешности при измерении одним и тем же методом и одними и теми же измерительными средствами, относят:

- погрешности метода или теоретические погрешности;

- инструментальные погрешности;

- погрешности, вызванные воздействием окружающей среды.

Погрешности метода происходят вследствие ошибок или недостаточной разработанности метода измерений. Например, принимая решение о годности вала по единичному измерению, можно допустить ошибку, так как не учитываются погрешности формы (отклонение от цилиндричности, круглости, профиля продольного сечения и др.). Поэтому для исключения такого рода систематических погрешностей в методике измерений рекомендуется проведение измерений в нескольких местах детали и взаимно-перпендикулярных направлениях. К погрешностям метода относят также влияние инструмента на свойства объекта (значительное измерительное усилие, изменяющее форму тонкостенной детали) или погрешности, связанные с чрезмерно грубым округлением результата измерения.

Инструментальные погрешности. Эти погрешности связаны с погрешностями средств измерения, вызванными погрешностями изготовления или износом составных частей измерительного средства.

Погрешности, вызванные воздействием окружающей среды, составляют температуру (например, измерения еще не остывшей детали), вибрации, не жесткость поверхности, на которую установлено измерительное средство и т. п.

Случайные погрешности. Это погрешности, принимающие при повторных измерениях различные, независимые по знаку и величине значения, не подчиняющиеся какой-либо закономерности.

Причин, вызывающих случайные погрешности, может быть много; например, колебание припуска на обработку, механические свойства материалов, посторонние включения, точность установки деталей на станок, точность средств измерения в заготовке, силы резания и т. д.

Для случайных погрешностей характерен ряд условий:

- малые по величине случайные погрешности встречаются чаще, чем большие;

- отрицательные и положительные относительно средней величины измерений, равные по величине погрешности, встречаются одинаково часто;

- для каждого метода измерений есть свой предел, за которым погрешности практически не встречаются.

Выявление случайных погрешностей особенно необходимо при точных, например, лабораторных измерениях. Влияние случайных погрешностей выражается в разбросе полученных результатов относительно математического ожидания, поэтому количественно наличие случайных погрешностей хорошо оценивается среднеквадратическим отклонением.

Грубые погрешности (промахи). Это погрешности, не характерные для технологического процесса или результата, приводящие к явным искажениям результатов измерения. Они сразу видны среди полученных результатов, так как полученные значения отличаются от остальных значений по совокупности измерений.

Такие погрешности возникают из-за неквалифицированного персонала при неправильном обращении со средством измерения, неверным отсчетом показаний, ошибками при записи или вследствие внезапно возникшей посторонней причины.

Известно, что наблюдение в физике преследует цель подтвердить старую теорию или послужить материалом для новой – это всегда попытка найти численное выражение наблюдаемой величины, т. е. измерить ее. Однако, квантовые законы микромира не всегда позволяют сделать это.

Во-первых, не коммутирующие величины невозможно получить в одном измерении с любой точностью из-за соотношений неопределенностей. Это связано с самими законами движения квантового объекта. Можно представить, что движение объекта может быть устойчивым, тогда некоторые величине. Они-то и могут принимать определенные значения.

Например, при стационарном вращении объекта сохраняется момент импульса. Величина этого импульса и его проекция на ось имеют определенные значения в этом типе движения. Отдельный акт измерения направлен на определение только одной величины. Причина этой невозможности заключается в том, что, во-вторых, любое измерение сразу разрушает то состояние, в котором находился квантовый объект, так что повторное наблюдение в этом состоянии невозможно.

В-третьих, нельзя заранее достоверно утверждать, что сейчас мы проведем наблюдение объекта в таком-то состоянии- до акта наблюдения состояние является неопределенным.

Поэтому измерение в микромире дают меньше информации, чем подобные им макроскопические измерения. Все связано с расстояниями, скоростью света и интенсивностью взаимодействия. Если в макромире мы можем сколь угодно совершенствовать наши приборы, изменяя их конструкцию и уменьшая размеры, повышая за счет этого точность результата, то в микромире у нас нет никаких других приборов, кроме частиц-«обитательниц» микромира. Исследуемый объект и прибор оказываются на одной ступеньке иерархической структуры материи. Прибор имеет только те свойства, что присущи микрочастицам.

Что касается измерения состояния, то оно не может быть каким угодно малым (бесконечно малым). Имеются в виду не координаты, энергия или подобные им динамические переменные, взятые по отдельности, а такая «композитная» величина, как действие. Качественно смысл действия можно понять, исходя из его физической размерности, которая равна произведению размерностей энергии и времени. Величина произведения зависит от обоих сомножителей, характерные значения которых очень разнообразны при разных условиях.

Макс Планк показал, что в процессах излучения и поглощения света атомами действие квантуется: его величина кратна некоторой конечной не равной постоянной ħ (постоянной Планка, равной 1,054·10^-34 Дж·с).

Эта величина является характерной величиной, так в атоме водорода электрон проходит 2/3 боровской орбиты, прежде чем действие измениться на ħ = 2р ħ. Любое измерение, будучи разновидностью взаимодействия, происходит с изменением действия на конечную величину, кратную ħ. Отсюда вытекает важное следствие: измерение (наблюдение) в микромире не может быть локальным, т. е. не может давать мгновенные характеристики объекта в некоторой точке.

Для наглядной иллюстрации рассмотрим движение маятника (рис. 3.5).

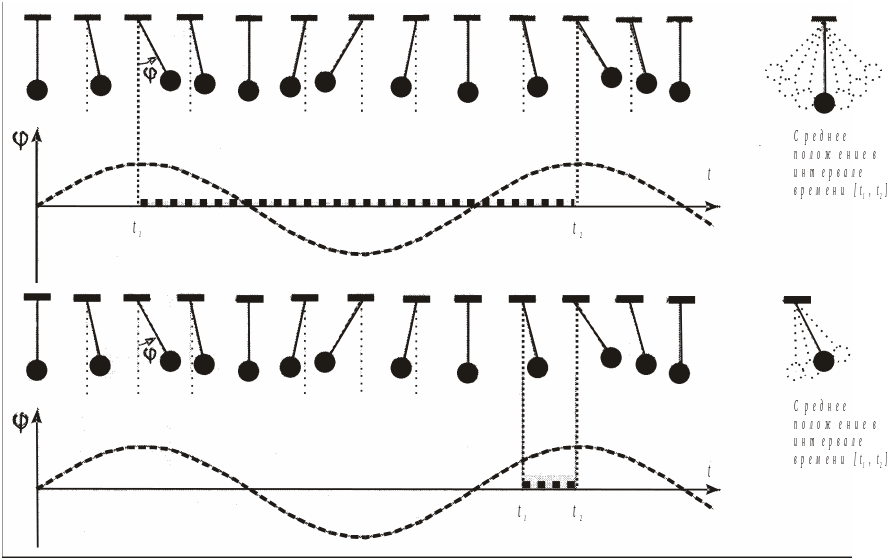
Рис. 3.5. Схема положения маятника в зависимости от величины и положения интервала измерения Δt

Легко видеть, что если считать измерение длящимся некоторое конечное время, а результат усредненным, то в зависимости от величины интервала измерения t₂ – t₁ его положения на оси времени (которое мы выбираем произвольно) получается различное положение (угол φ) маятника.

Чем меньше время измерения, тем ближе результат к мгновенному положению, даваемому теорией. У уменьшения Δt должен быть конечный предел, не равный нулю. Всякий раз Δt может быть разным, но таким, чтобы действие оказывалось меньше ħ.

Это не ставит предел точности измерения, так как действие является интегралом от функции таких взаимно дополнительных величин, как энергия, время, а также импульс и координаты.

Чтобы повысить пространственное разрешение частицы прибора, ей просто придают больший импульс (разгоняют).

Если прибором является электромагнитная волна, которая и так движется с предельной скоростью, то выбирают волну короче, с большей частотой. Например, если мы облучим атом водорода жестким излучением (γ-лучами), то оно может провзаимодействовать с электроном и тем самым указать его координаты значительно точнее.

При этом атом лишится этого электрона. Часто требуется знать, чему равны несколько величин в одни и те же моменты времени, т. е. их синхронное поведение.

Например, в цепи переменного синусоидального тока элементы нагрузки могут быть разного характера: реактивные элементы (индуктивность L и емкость С) имеют свойство смещать фазу напряжения относительно тока, тогда как на активном сопротивлении R этого не происходит. Зато в целом за период на R теряется часть энергии (выделяется в виде тепла), а на L и С ее баланс равен нулю – сколько поглотят за полпериода столько потом и отдадут. Индуктивность и емкость могут оказывать большое влияние на динамику работы цепи, и степень этого влияния можно оценить из синхронного изменения двух переменных – напряжения и тока. В цепи переменного тока принципиальных препятствия нет.

Совсем по-другому обстоит дело с измерениями в микромире. Для измерения некоторой величины процесс измерения «ориентируется» определенным образом, именно под эту величину (специальные приборы, специальные методики), а сразу после измерения исходного состояния уже нет – его разрушает наблюдение двух и более динамических переменных невозможно в буквальном смысле.

Пример. Наблюдения синусоидального тока на однолучевом осциллографе покажут похожие синусоиды I(t), U(t) на всех элементах цепи, и активных и реактивных. При этом на резисторе энергия теряется, а на конденсаторе и на катушке – нет, хотя они интегрируются в мощность P(t) = U I по периоду. А наблюдения за током и напряжением синхронно на двухлучевом осциллографе покажет смещение фаз между U и I на катушке и конденсаторе по времени друг относительно друга (рис. 3.6).

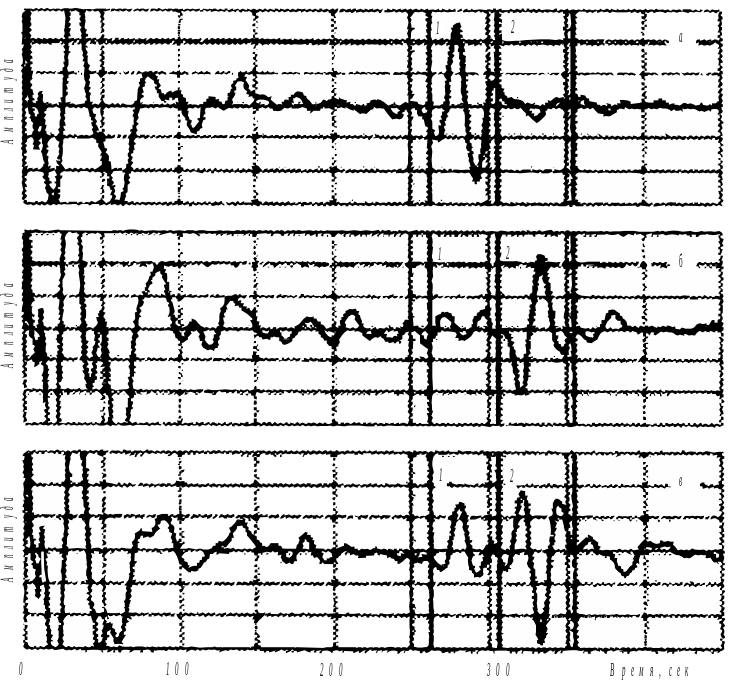
Рис. 3. 6. Три синхронных характеристики одного процесса

Все погрешности происходят в определенном диапазоне, который определен пределами измерений. Существуют нижний и верхний пределы. Они устанавливаются эмпирическим способом (экспериментально).

При определении нижнего или верхнего пределов измерения учитываются следующие положения:

- физическая состоятельность процесса или явления (есть или его нет);

- физическое преобразование (энергетические переходы);

- осмысленность измерения (ниже нижнего предела измерить нет возможности, а выше верхнего – теряется смысл измерения или измерения очень дороги и наоборот).

Пример. Пределы измерения температуры воды: нижний – 0 ^○С, а верхний – 100 ^○С. При температуре 0 ^○С и ниже вода приобретает твердое состояние (лед), т. е. происходит изменение состояния вещества за счет изменения энергетического преобразования. Ниже температуры 0 ^○С измерение теряет смысл, за исключением получения сравнительных величин другого вещества. При температуре выше 100 ^○С вода превращается в пар – газообразное агрегатное состояние также за счет энергетического перехода. Выше 100 ^○С будут измерения уже пара, а не жидкости.

При измерении твердости резин применяется методика внедрения металлической иглы в толщу вещества, предложенная Шором. Насколько глубоко внедрится игла в резину, настолько судят о повышении твердости. Пределы измерения от 0 до 100 усл. ед. по Шору. Твердость меньше 0 означает, что исследуемое вещество является жидкостью, а не резиной и «твердость» измеряется другим методом и обладает другой размерностью.

Твердость выше 100 усл. ед. по Шору показывает, что измеряемое вещество относится к другому классу полимеров (эбонит, пластмассы) и поэтому требует также другой методики измерения со своими единицами измерения.

Существуют пределы оценок например, органолептических параметров качества продукции в баллах. Так, вкус пищевого продукта оценивается от 1 до 10 баллов. Наивысший балл соответствует наилучшей оценке, а наименьший – наихудшей.

Контрольные вопросы:

1.Что устанавливает статистическая механика?

2. Что такое флуктуации, возникающие в самом измерительном приборе?

3. Что такое дробовой эффект, эмиссия?

4. В чем смысл принципа Паули?

5. Что такое статистика Бозе-Эйнштейна?

6. Что такое фермионы, адроны, мезоны, лептоны, кварки, фотоны, гравитоны?

7. Каковы этапы познания строения вещества?

8. В чес заключается фундаментальный принцип вещества?

9. Что дает эффект динамической стабильности?

10. В чем заключается физическое обеспечение стабильности объектов?

11. В чем заключается техническое обеспечение стабильности объектов?

12. Что является основой технической диагностики?

13. Что такое «Объект исправен»?

14. Что такое «Объект работоспособен»?

15. Как классифицируются погрешности?

16. Как устанавливается предел измерения?

17. Что такое систематические погрешности?

18. Что такое инструментальные погрешности?

19. Что такое грубые погрешности (промахи)?

20. Почему измерение (наблюдение) в микромире не может быть локальным?