2. Измерения и измерительные системы

2.1. Измерения физических величин.

Физическая величина (ФВ) – одно из свойств физического объекта (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого их них.

Любое измерение заключается в сравнении значения измеряемой величины с другим, принятым за единицу.

Измерение ФВ – совокупность операций по применению технического средства, хранящего единицу ФВ, обеспечивающих нахождение соотношения (в явном, или неявном виде) измеряемой величины с её единицей, и получение значения этой величины.

Прямое измерение – измерение, при котором искомое значение физической величины получают непосредственно.

Косвенное измерение – определение искомого значения ФВ на основании результатов прямых измерений других ФВ, функционально связанных с искомой величиной.

Единица измерения является мерой, с помощью которой измеряется та или иная физическая величина. Это измерение представляет собой прямое или косвенное сравнение физических характеристик с соответствующими (физически подобными) эталонами, принятыми за единицу и называемыми единицей измерения.

Будем говорить, что физическая величина G измерена, если известно, сколько раз в G содержится некоторая единица. Это и есть числовое значение {G} величины G. Если символически обозначить через [G] размерность величины G, то

G={G}[G].

Величины, численное значение которых зависит от принятых масштабов, т. е. от системы единиц измерения, называются размерными или именованными величинами. Величины, численное значение которых не зависит от применяемой системы единиц измерения, называются безразмерными или отвлеченными величинами. Длина, время, сила, энергия, момент силы могут служить примерами размерных величин. Углы, отношение двух длин, отношение квадрата длины к площади, отношение энергии к моменту силы − примеры безразмерных величин.

Однако подразделение величин на размерные и безразмерные является до некоторой степени условным. Так, например, угол мы только что назвали безразмерной величиной. Но известно, что углы можно измерять в радианах, в градусах, в долях пря­мого угла, т. е. в различных единицах. Следовательно, число, определяющее угол, зависит от выбора единицы измерения. Поэтому угол можно рассматривать и как величину размерную. Определим угол как отношение стягивающей его дуги окружности к радиусу; этим самым будет определена однозначно единица измерения угла — радиан. Если теперь во всех системах единиц измерения измерять углы только в радианах, то угол можно будет рассматривать как безразмерную величину. Точно так же, если для длины ввести единую фиксированную единицу измерения во всех системах единиц измерения, то после этого длину можно будет считать безразмерной величиной. Но фиксирование единицы измерения для углов удобно, а для длин неудобно. Это объясняется тем, что для геометрически подобных фигур соответствующие углы одинаковы, а соответствующие длины неодинаковы, и поэтому в различных вопросах выгодно выбирать за основную длину различные расстояния.

Ускорение обычно рассматривается как размерная величина, размерность которой есть длина, деленная на квадрат времени. Во многих вопросах ускорение силы тяжести g, равное ускорению при падении тел в пустоте, можно считать постоянной величиной (9,81 м/сек²). Это постоянное ускорение g можно выбрать в качестве фиксированной единицы измерения для ускорений во всех системах единиц. Тогда любое ускорение будет измеряться отно­шением его величины к величине ускорения силы тяжести. Это отношение называется перегрузкой, численное значение которой не будет меняться при переходе от одних единиц измерения к другим. Следовательно, перегрузка является величиной безразмерной. Но в то же время перегрузку можно рассматривать и как размерную величину, именно как ускорение, когда за единицу измерения принято ускорение, равное ускорению силы тяжести. В этом последнем случае мы предполагаем, что за единицу измерения перегрузки − ускорения − можно взять и такое ускорение, которое не равно ускорению силы тяжести.

С другой стороны, величины отвлеченные (безразмерные) в общепринятом смысле этого слова можно выражать с помощью различных чисел. В самом деле, отношение двух длин можно выразить не только в виде обычного арифметического частного, но и в процентах, а также другими способами.

Таким образом, понятия размерных и безразмерных величин являются относительными понятиями. Мы вводим некоторый, запас единиц измерения. Тогда величины, для которых единицы измерения одинаковы во всех принятых системах единиц измерения, мы будем называть безразмерными.

Величины же, для которых в опытах или в теоретических исследованиях фактически или потенциально (явно или неявно) допускаются различные единицы измерения, мы будем называть размерными. Из этого определения вытекает, что некоторые величины можно рассматривать в одних случаях как размерные, а в других — как безразмерные.

Различные физические величины связаны между собой определенными соотношениями. Поэтому если некоторые из этих величин принять за основные и установить для них какие-то единицы измерения, то единицы измерения всех остальных величин будут определенным образом выражаться через единицы измерения основных величин. Принятые для основных величин единицы измерения будем называть основными или первичными, а все остальные — производными или вторичными.

На практике достаточно установить единицы измерения для трех величин, каких именно, — это зависит от конкретных условий той или иной задачи; в разных вопросах целесообразно за основные единицы брать единицы измерения различных величин. Так, в физических исследованиях удобно за основные единицы взять единицы длины, времени и массы, а в технике — единицы длины, времени и силы. Но можно было бы взять за основные единицы измерения также единицы скорости, вязкости и плотности и т. п.

Большим распространением пользуются физическая и техническая системы единиц измерения. В физической системе за основные единицы измерения приняты сантиметр, грамм-масса и секунда (отсюда сокращенное название — система единиц CGS), а в технической системе — метр, килограмм-сила и секунда (отсюда сокращенное название — система единиц MKS).

С 1 января 1963 года государственным стандартом СССР (ГОСТ 9867) введена единая Международная система единиц СИ (SI — System International).

В системе СИ за основные механические единицы измерения приняты метр, килограмм-масса и секунда; за единицу силы тока принят ампер, за единицу термодинамической температуры — кельвин, за единицу силы света — кандела и за единицу количества вещества — моль.

Как только установлены основные единицы измерения, единицы измерения для других механических величин, например, для силы, энергии, скорости, ускорения и т. п., получаются авто­матически из их определения.

Выражение производной, единицы измерения через основные единицы измерения называется размерностью.

В дальнейшем для обозначения размерности какой-нибудь величины а мы будем пользоваться символом [а], введенным Максвеллом. Размерность записывается символически в виде формулы.

Например, для размерности силы F в физической системе будем писать

[F]=MLT^-2 или MLT^-2=K,

где символ единицы длины обозначается буквой L, символ единицы массы — буквой М, символ единицы времени — буквой Т (в технической системе единиц символ единицы силы обозначается буквой К).

О размерности можно говорить только применительно к определенной системе единиц измерения. Например, размерностью площади будет L², размерностью скорости L/T, размерностью силы в физической системе единиц будет ML/T², а в технической системе − К.

Число основных единиц измерений не обязательно должно быть равно трем. Вместо трех можно брать и большее число основных единиц. Так, например, опытным путем можно установить независимо друг от друга единицы измерения для четырех величин: длины, времени, массы и силы.

Нетрудно видеть, что число основных единиц измерения можно взять и меньшим трех. В самом деле, все силы мы можем сравни­вать с силой тяготения, хотя это неудобно и противоестественно в тех вопросах, в которых сила тяготения не играет роли.

Наконец, мы можем рассматривать все физические величины как безразмерные. В этом случае исключается возможность употребления различных систем единиц измерения. Получается одна-единственная система единиц измерения, основанная на выбранных физических постоянных (например, на гравитационной постоянной, скорости света и коэффициенте вязкости воды), значения которых принимаются в качестве абсолютных универсальных постоянных.

Таким образом, мы видим, что при выборе способа построения системы единиц существует большой произвол.

Однако на практике приходится считаться с целым рядом требований, которые существенно ограничивают этот произвол.

Слишком большое число основных единиц было бы неудобно из-за появления размерных коэффициентов во многих физических формулах и необходимости установления большого числа эталонов.

Слишком малое число основных единиц приводит к тому, что построенные на них производные единицы оказываются неудобными для использования на практике. Практически используются системы, в которых число основных единиц колеблется от трех до семи.

Зависимость единицы измерения производной величины от единиц измерения основных величин может быть представлена в виде формулы. Эта формула называется формулой размерности, и ее можно рассматривать как сжатое определение и характеристику физической природы производной величины.

О размерности можно говорить только применительно к определенной системе единиц измерения. В разных системах единиц измерения формула размерности для одной и той же величины может содержать различное число аргументов и может иметь различный вид. В системе единиц измерения CGS формулы раз­мерности всех физических величин имеют вид степенного одночлена

L^l M ^m T ^t.

Такой вид формулы размерности определяется следующим физическим условием: отношение двух численных значений какой-нибудь производной величины не должно зависеть от выбора масштабов для основных единиц измерения. Например, будем ли мы измерять площадь в квадратных метрах или квадратных сантиметрах, отношение двух площадей, измеренных в квадратных метрах, будет таким же, как и отношение этих же площадей, измеренных в квадратных сантиметрах. Для основных величин это условие является составной частью определения единицы измерения и удовлетворяется само собой.

Пусть мы имеем какую-нибудь размерную производную величину у; для простоты примем сначала, что величина у является геометрической и поэтому зависит только от длин, следовательно,

y= f(x₁, x₂,…, x_n),

где х₁, х₂,…, х_п − некоторые расстояния. Обозначим через у' то значение величины y, которое соответствует значениям аргументов х’₁, х’₂,…, х’_п

y’= f(x’₁, x’₂,…, x’_n).

Численное значение y, а также у', зависит от единицы измерения для расстояний х₁, х₂,…, х_п. Уменьшим эту единицу или масштаб расстояний в α раз. Тогда согласно сформулированному выше условию мы должны иметь

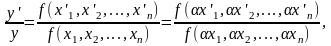(1)

т. е. отношение y'/y должно быть одинаковым при любом значе­нии масштаба длин α. Из равенства (1) получаем

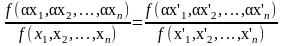или

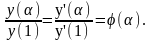(2)

Следовательно, отношение численных значений производной гео­метрической величины, измеренной в разных масштабах длины, зависит только от отношения масштабов длин.

Из соотношения (2) легко найти вид функции φ(α). В самом деле, имеем

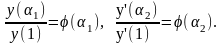
Отсюда получаем

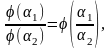(3)

так как при x'₁ = х₁α₂ , х'₂ = х₂а₂, .... ,х'_n=х_п а₂ имеем

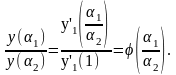
Дифференцируя уравнение (3) по α₁ и полагая α₁ = α₂ = α, получаем

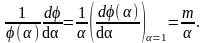
Интегрируя, найдем

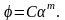
Так как при α = 1 имеем φ =1, то С = 1; следовательно,

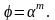
Этот вывод справедлив для любой размерной величины, зависящей от нескольких основных величин, если мы будем менять только один масштаб.

Нетрудно видеть, что если изменяются масштабы α, β, γ трех основных величин, то функция φ будет иметь вид

φ= α^m βⁿ γ^t.

Этим доказывается, что формулы размерности физических величин должны иметь вид степенных одночленом.

Будем говорить, что величины а₁,а₂,а₃,..., а_k имеют независимые размерности, если формула, выражающая размерность одной из этих величин, не может быть представлена как комбинация в виде степенного одночлена из формул размерности для других величин.

Например, размерности длины L, скорости L /T и энергии ML²/T² независимы; размерности длины L, скорости L/T и ускорения L/T² зависимы. так как между размерностями этих последних величин имеет место соотношение [l][w] = [²].

Среди механических величин обычно имеется не более трех с независимыми размерностями.

Физические закономерности, устанавливаемые теоретически или непосредственно из опыта, представляют собой функциональные зависимости между величинами, характеризующими исследуемое явление.

Численные значения этих размерных физических величин зависят от выбора системы единиц измерения, не связанной с существом явления. Поэтому функциональные зависимости, выражающие собой физические факты, которые не зависят от системы единиц измерения, должны обладать некоторой специальной структурой.

Пусть мы имеем размерную величину а, которая является функцией независимых между собой размерных величин а₁, a₂,..., a_n

,

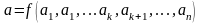некоторые из этих параметров в рассматриваемом процессе могут быть переменными, другие — постоянными.

Имеет место теорема (П-теорема).

Связь между n+1 размерными величинами а, а₁, a₂,..., a_n , независимая от выбора системы единиц измерения, принимает вид соотношения между n+1−к величинами П, П_k+1, . . ., П_n , представляющими собой безразмерные комбинации из n+1 размерных величин.

Доказательство.

Разобьем аргументы а₁, a₂,..., a_n на две группы следующим образом: первые величины а₁, a₂,..., a_k (0  k  n) имеют независимые размерности, а размерности остальных параметров а_k+1, a_k+2,..., a_n зависимы от них. (Если размерности всех определяющих параметров независимы, то k = n, если все определяющие параметры безразмерны, то k = 0.)

Примем k независимых величин а₁, a₂,..., a_k за основные величины и введем для их размерностей обозначения

[а₁] = А₁, [а₂] = А₂,…, [а_k] = А_k.

Размерности остальных величин будут иметь вид

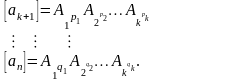
Очевидно, что размерность определяемой величины а определяется через размерности определяющих параметров первой группы а₁, a₂,..., a_k:

.

Изменим теперь единицы измерения величин а₁, a₂,..., a_k соответственно в α₁, α₂,…, α_k раз; численные значения этих величин и величин а, а_k+1, . . ., а_п в новой системе единиц будут соответственно равны:

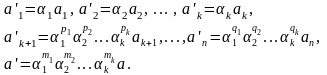
В новой системе единиц измерения это соотношение примет вид

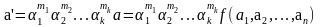
или, с другой стороны,

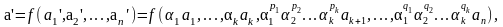получаем равенство

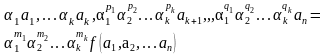
Это равенство показывает, что функция f обладает свойством однородности относительно масштабов α₁, α₂,…, α_k. Масштабы α₁, α₂,…, α_k произвольны.

Воспользуемся выбором этих мас­штабов для сокращения числа аргументов у функции f.

Положим:

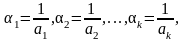
т. е. выберем систему единиц измерения таким образом, чтобы значения первых k аргументов в левой части соотношения (5) равнялись единице. (Для простоты мы принимаем, что параметры a₁, a₂,…, a_k конечны и отличны от нуля. Последующие выводы распространяются на случаи, когда a₁, a₂,…, a_k могут обращаться в нуль или бесконечность, если функция f при этих значениях аргументов непрерывна.) Иначе говоря, используя то обстоятельство, что известное соотношение согласно предположению не зависит от системы единиц измерения, мы устанавливаем систему единиц измерения так, чтобы k аргументов у функции f имели фиксированные постоянные значения, равные единице.

Получим

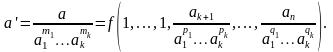
Введем обозначения

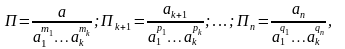
где а, а₁, а₂, . . ., а_п суть численные значения рассматриваемых величин в первоначальной системе единиц измерения.

Нетрудно видеть, что значения П, П_k+1, . . ., П_n не зависят от выбора первоначальной системы единиц измерения, так как они имеют нулевую размерность относительно единиц измерения A₁, А₂,…, А_k. Очевидно также, что значения П, П_k+1, . . ., П_n вообще не зависят от выбора системы тех единиц измерения, через ко­торые выражаются k единиц измерения для величин a₁, a₂,…, a_k.

Следовательно, эти величины можно рассматривать как безразмерные.

Пользуясь новыми обозначениями, начальное соотношение можно представить в виде

П = f (1, 1,..., П_k+1, .... П_n),

Таким образом, связь между величинами а, а₁, а₂, . . ., а_п, независимая от выбора системы единиц измерения, принимает вид соотношения между n+1−к величинами П, П_k+1, . . ., П_n, представляющими собой безразмерные комбинации из n+1 размерных величин. Доказательство закончено.

Всякое физическое соотношение между размерными величинами можно сформулировать как соотношение между безразмерными величинами. В этом и заключается источник полезных приложений метода теории размерности к исследованию механических задач.

2.2. Классические измерительные системы и их структура.

Структура классических измерительных систем представлена на рис. 2.1.

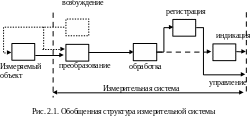
Обычно измерительной системой называют всю совокупность измерительных приборов и устройств, необходимых для проведения измерения. При этом под «системой» понимался как одиночный прибор, так и сложная измерительная установка. Далее мы детализируем внутреннюю конфигурацию или структуру измерительной системы, рассмотрим функциональную внутреннюю структуру измерительной системы (см. рис. 2.1).

1. Источник возбуждения. В тех случаях, когда измеряемая величина не является активной, необходимо воспользоваться источником возбуждения, который будет оказывать воздействие на измеряемый объект. Тогда отклик объекта (вместе с самим воздействием) будет содержать желаемую информацию. Если же измеряемый объект сам порождает сигнал, уже содержащий желаемую информацию, то во внешнем возбуждении нет надобности.

2. Преобразование. Когда измеряемая величина имеет электрическую природу ее не надо преобразовывать. Когда же нужно измерить неэлектрические параметры или переменные, такие как жесткость, тепловое сопротивление, смещение и т. д., чаще всего применяется того или иного рода датчик или преобразователь. В датчике входной параметр или переменная трансформируются в электрический выходной сигнал, который несет информацию об исходной измеряемой величине.

3. Обработка. Как правило, электрический сигнал на выходе датчика не пригоден для того, чтобы быть непосредственно представленным наблюдателю. Часто бывает необходимо сначала подвергнуть его обработке того или иного вида (усилению, фильтрации, коррекции нелинейности датчика и др.).

4. Регистрация. После обработки выходной сигнал можно сразу представить наблюдателю, а можно временно сохранить в памяти и воспользоваться им позднее, т. е. зарегистрировать результата измерения.

5. Индикация. Сразу после обработки сигнал может быть представлен наблюдателю (минуя регистрацию).

Устройство, предназначенное для представления результатов измерения человеку-наблюдателю, мы назвали «устройством индикации» (дисплеем).

6. Управление. Бывает так, что результат измерения не регистрируется и не воспроизводится средством индикации, а непосредственно используется для управления каким-то процессом. Целью управления процессом является такое регулирование, при котором выходной продукт соответствует определенным требованиям.

Не во всякой измерительной системе имеются все шесть подсистем, указанных на рис. 2.1. Подсистемы не обязательно должны следовать в указанном порядке. Ниже рассмотрим подсистемы, на которые мы разбили измерительную систему общего вида.

Информация, которую мы хотим получить от измеряемого объекта, не всегда имеет форму активной информации. В тех случаях, когда измеряемая величина не является активной, необходимо воспользоваться источником возбуждения, который будет оказывать воздействие на измеряемый объект. Тогда отклик объекта (вместе с самим воздействием) будет содержать желаемую информацию. Если же измеряемый объект сам порождает сигнал, уже содержащий желаемую информацию, то во внешнем возбуждении нет надобности.

Часто параметр или переменная величина, которую мы хотим измерить, имеет электрическую природу. Когда нужно измерить неэлектрические параметры или переменные, такие как жесткость, тепловое сопротивление, смещение и т. д., чаще всего применяется того или иного рода датчик или преобразователь, и система в целом не остается чисто механической или тепловой измерительной системой. В датчике входной параметр или переменная трансформируются в электрический выходной сигнал, который несет информацию об исходной измеряемой величине.

Большим достоинством такого преобразования в электрический сигнал является тот факт, что оно дает нам возможность в дальнейшем обрабатывать информацию с помощью электроники, а это совсем не дорогой и гибкий способ обработки. Например, в таком виде информацию легко передавать на большие расстояния при минимальном мешающем действии окружающей среды. Передавая измерительную информацию, мы можем осуществлять измерения на расстоянии (это называют телеметрией). Особенно полезно это для измерений в недоступных местах или в агрессивной среде, например, под водой (в океанографии), в атмосфере (в метеорологии) или при измерении большого числа объектов, которые разнесены далеко друг от друга (например, измерения в пищевой или нефтяной промышленности).

Иногда передача информации осуществляется другими, неэлектрическими средствами. В некоторых отраслях обрабатывающей промышленности, где имеют дело с воспламеняющимися веществами, для передачи информации применяют пневматическую телеметрию.

Данные измерений в этом случае передаются по тонким трубкам посредством давления газа.

Если телеметрический канал оборван (или в нем произошло короткое замыкание), то в некоторых случаях внезапное появление нуля на выходе может быть опасным, когда известно, что измеряемая величина заведомо не равна нулю. По этой причине часто определенное значение тока или напряжения покоя принимают за нулевое значение, называя его «живым нулем». Когда «живой нуль» нарушается, неполадки обнаруживаются и активизируется механизм, обеспечивающий безопасность при возникновении неполадок, чтобы вернуться к безопасным условиям работы.

В телеметрической системе измерительная информация не обязательно бывает представлена в виде величины электрического потенциала или тока. Иногда, чтобы сделать систему менее чувствительной к возмущениям, информацию помещают в частоту сигнала или в длительность импульсов, следующих с постоянной частотой, или даже передают ее в цифровом виде. Эти методы передачи обладают большой помехоустойчивостью и лучше защищены от шумов.

Как правило, электрический сигнал на выходе датчика не пригоден для того, чтобы быть непосредственно представленным наблюдателю. Часто бывает необходимо сначала подвергнуть его обработке того или иного вида (усилению, фильтрации, коррекции нелинейности датчика и др.).

После такой обработки сигнал может быть представлен наблюдателю. Мы можем показать результат человеку-наблюдателю или управлять посредством результирующего выходного сигнала механическим наблюдателем (автоматом). Выходной сигнал можно также временно сохранить в памяти и воспользоваться им позднее.

В этом случае говорят о регистрации результата измерения.

Иногда различные подсистемы могут быть объединены в один измерительный прибор, но могут быть также реализованы порознь, как отдельные устройства. Магнитофон, например, является лишь регистрирующим прибором, тогда как перьевой самописец служит как для регистрации результата измерения, так и в качестве устройства индикации. Ниже рассмотрим подсистемы, на которые мы разбили измерительную систему общего вида.

Измерительный сигнал - энергетическое физическое явление, несущее информацию. Предполагается, что такой сигнал относится к соответствующей области физики или к ее определенному разделу.

Например, механический, тепловой, электрический и магнитный сигналы принадлежат каждый к своей собственной соответственной физической области. Чтобы обеспечить перенос из одной физической области в другую, должна существовать возможность отображать сигналы из одной физической области на сигналы из другой области.

Такое отображение осуществляют «преобразователи», которые способны энергетическое физическое явление одного рода (из одной области) преобразовывать в явление другого рода (в другой области). При преобразовании должна сохраняться информация, содержащаяся в исходном энергетическом явлении.

Такие сохраняющие информацию энергетические преобразователи называют измерительными датчиками.

Кроме отображения сигналов, принадлежащих различным областям, друг на друга, необходимо также иметь возможность отображать друг на друга сигналы из одной и той же области.

В этом случае энергетическое явление преобразуется в подобное ему энергетическое явление с сохранением соответствующей информации, содержащейся в исходном явлении. Может понадобиться увеличить мощность явления (усиление мощности), или опустить какую-то ненужную информацию (фильтрация).

Происходящие в веществе физические эффекты, используемые для отображения сигналов из различных областей называют эффектами переноса, тогда как для отображения сигналов в пределах одной области используются происходящие в веществе эффекты, называемые прямыми.

Например, эффект переноса:

- из электрической области в тепловую — эффект Пельтье;

- из тепловой области в электрическую — эффект Зеебека;

- из магнитной области в электрическую — эффект Холла.

Примеры прямых эффектов, происходящих в веществе: в электрической области — электрическое сопротивление; в механической области — упругость.

В отношении свойства датчиков преобразовывать энергию различают два типа датчиков: пассивные и активные.

Пассивными являются такие датчики, которые функционируют без потребления энергии от вспомогательного источника (см. рис. 2. 2, а).

Средняя мощность сигнала на выходе Р₀ является частью средней мощности Р объекта отдаваемой измеряемым объектом. Однако физически реализуемое преобразование энергии всегда сопровождается потерями (мощности Р_пот), поэтому:

Р_{объекта} = Р_пот + Р₀

Возможно, в принципе, накопление энергии в датчике на короткое время. Следовательно, приведенное выше соотношение справедливо только для значений, являющихся результатом усреднения на протяженном интервале времени.

Когда измеряемый объект нельзя сильно нагружать, то есть, он может отдавать лишь очень малую входную мощность, существенным становится коэффициент полезного действия (КПД) пассивного датчика.

а б

а б

Рис. 2. 2. Пассивный и активный датчики:

Р_{объекта}, — мощность на входе, Р₀ — мощность на выходе, Р_пот, — мощность, которая теряется в процессе преобразования, P_c, — мощность управляющего воздействия, Р_ps — мощность вспомогательного источника; а - пассивный датчик, б - активный датчик.

Конечно, КПД процесса преобразования, не так важен в случае, когда на входе имеется большая мощность. Все механические вольтметры, амперметры и ваттметры являются примерами этого класса пассивных датчиков. В них электрическая энергия преобразуется в механическую энергию в форме потенциальной энергии сжатой пружины подвижной системы измерительного прибора.

Активными являются такие датчики, которым требуется вспомогательный источник питания (см. рис. 2. 2, б).

Выходная мощность датчика Р₀, почти полностью берется из этого вспомогательного источника питания, отдающего мощность Р_ps .

Мощность, которую отдает измеряемый объект, практически равна нулю. Требуется лишь совсем малая мощность Р_c чтобы управлять выходной мощностью датчика (на рис. 2. 2, б) этот процесс преобразования схематически изображен в виде заслонки). Подавая мощность от вспомогательного источника можно реализовать датчики с усилением, обладающие очень высокой чувствительностью.

Как уже говорилось, во многих измерительных системах используются датчики, преобразующие неэлектрические сигналы в электрические, поскольку обработка и передача сигналов в электрической области сравнительно просты. Поэтому мы ограничим наше рассмотрение датчиками, которые отображают сигналы из различных физических областей на сигналы в электрической области, а также обратными преобразователями, которые переводят электрический сигнал в неэлектрическую величину.

Датчики первой категории нужны на входе измерительной системы. Поэтому они называются входными или измерительными датчиками.

Обратные преобразователи нужны на выходе измерительной системы для целей индикации и регистрации данных или для управления другими процессами. Поэтому их называют выходными датчиками или исполнительными механизмами.

К сожалению, не существует единой терминологии в мире датчиков. Их называют по разному: сенсор, чувствительный элемент, измерительный преобразователь и т. п.

Классификацию датчиков часто производят по той величине, которая измеряется с их помощью (датчик смещения, акселерометр, тензодатчик и т. д.), или по принципу действия (емкостной датчик смещения, пьезоэлектрический акселерометр, резистивный тензодатчик и т. д.).

Одной из причин преобразования неэлектрических сигналов в электрические является большое разнообразие и гибкость методов обработки, предлагаемых современной электроникой.

Обычно электронный измерительный сигнал или выходной сигнал датчика сам по себе не пригоден для непосредственной индикации, регистрации или управления машиной и поэтому должен быть сначала преобразован. Обработка сигнала может быть линейной, частотно-зависимой (фильтрация) или (квази-) частотно-независимой (усиление, ослабление). Возможно также выполнение нелинейных операций (выпрямление, определение среднеквадратичного значения, аналого-цифровое преобразование и др.).

Устройства индикации. Устройство, предназначенное для представления результатов измерения человеку-наблюдателю, мы назвали «устройством индикации» (дисплеем). Устройства индикации не обязательно должны быть аналоговыми (как, например, электронный луч, рисующий на экране осциллографа), они могут также быть цифровыми (например, алфавитно-цифровой дисплей или светящиеся элементы индикации). Как мы уже видели, устройства индикации рассчитаны на визуальное наблюдение и потому являются электрооптическими преобразователями. Чтобы избежать больших ошибок считывания и интерпретации, аналоговые устройства индикации должны быть особенно хорошо согласованы с потребностями наблюдения. Эта проблема решается, в частности, путем применения гибридных устройств индикации. Например, в осциллографе тем же электронным лучом, который рисует форму сигнала, можно отобразить на экране такую информацию, как чувствительность, масштаб по оси времени и др. Важно осуществить сопряжение цифрового устройства индикации с наблюдателем, чтобы наблюдение не было утомительным и по этой причине не допускались промахи (нужно минимизировать блики, обеспечить высокую контрастность, использовать приятные цвета, четкие и разборчивые символы и т. д.).

Регистрация данных. Данные регистрируются для того, чтобы они были доступны позднее, например, для представления наблюдателю в более удобное время. К регистрации часто прибегают в тех случаях, когда собирается большое число результатов измерений и нужно облегчить производимый вслед за этим анализ полученных результатов.

Возьмем, например, «черный ящик», имеющийся на каждом самолете; записанные в нем данные считываются всегда позже, когда возникает интерес к выполненным ранее измерениям (после того, как произойдет авария).

Другим поводом для регистрации данных служит желание предотвратить необходимость повторения измерений (в частности, когда опыты крайне дороги, например, эксперименты по столкновению частиц). Для того, чтобы облегчить интерпретацию результатов измерений, часто осуществляют графическую запись.

Примерами таких записей являются х-t и х- у диаграммы, а также графики в полярных координатах. При таком способе регистрации результатов измерений раскрываются их структура и соотношение между ними, благодаря чему интерпретация упрощается. Например, электрическая активность сердца регистрируется в виде электрокардиограмм, то есть в форме графиков в координатах х-t. В таком графике специалисту легко распознать характерные зубцы или возможные нарушения.

Данные можно регистрировать в аналоговом или цифровом виде; например, графическая запись осуществляется самописцем, возможна магнитная запись на ленту.

Управление, обратная связь. Бывает так, что результат измерения не регистрируется и не воспроизводится средством индикации, а непосредственно используется для управления каким-то процессом.

Целью управления процессом является такое регулирование, при котором выходной продукт соответствует определенным требованиям. Измеряются один или большее число параметров процесса, и регулирование осуществляется таким образом, чтобы уменьшить различие между измеряемыми величинами и заданными наперед значениями. Если управление основано на измерении такого параметра процесса, на котором не отражается результирующее изменение характеристик процесса, то считается, что регулирование процесса осуществляется по принципу автоматического управления «вперед» (разомкнутая система управления).

Однако в том случае, когда управление базируется на измерениях, результаты которых зависят от предшествующих управляющих воздействий, возникает замкнутый контур (который в отдельных случаях, в принципе, может приводить к неустойчивости). Этот последний метод управления процессом носит название управления с обратной связью.

2.3. Принципиальная невозможность устранения неопределенности измерений.

Неопределенность – это принципиальное отрицание определения величины параметра, а не результат влияния помех или ошибки измерения, подчиненных вероятностным законам, если их точнее воздействие не известно. Неопределенность, которую нельзя устранить, имеет место и в классической механике, она просто объясняется и легко воспринимается. Это случай, когда ограничена разрешающая способность конкретного измерительного инструмента: слишком велика при измерении цена деления, т. е. измерение осуществляется с помощью определенного шаблона, а требуется точность более высокая, чем та, что обеспечивается размерами или другими параметрами шаблона. Ни у кого, например, не вызывает удивления, что величина разрешения, достигаемая микроскопом, ограничена длиной волны в луче освещения. Эта неопределенность не связана с нашим незнанием причины погрешности, тем более, что этой причины не существует – у нас нет методики или инструмента для более точного определения измеряемого параметра.

Принципы неопределенности и дополнительности – это закономерное отражение свойств материального мира. При выработке этих принципов проявилась старая болезнь науки – антропометризм. Окружающий мир подразделяется по человеческой мерке на микромир – мир объектов, малых, по сравнению с человеком, на мир объектов, сравнимой с ним величины, и на мир больших пространств и размеров – макромир, космос. При этом забывается, что колоссальное – огромно и длительно, лишь в сравнении с нашей мизерностью и быстротечностью, а малое – ничтожно и мимолетно, лишь рядом с нашей пространственностью и долговременностью. Тем не менее, так подразделенные миры наделяются координальными различиями. Так, современная физика приписывает микромиру свойства частичной непознаваемости и иррациональности, одним из аспектов которых является принцип неопределенности, сформулированный В. Гейзенбергом и расширенный до понятия дополнительности Н. Бором. Теория измерительных приборов, главным содержанием которой является учение о точности, причинах возникновения ошибок и методах их уменьшения, базируется на ряде физических принципов, которые составляют аксиоматику измерительной техники. Эти аксиомы (или принципы) определяют принципиальные или практические ограничения на достижимые точности.

Принципиальные ограничения обусловлены дискретностью измеряемых величин (например, нельзя измерить заряд, меньший заряда электрона) или флуктуациями, определяемыми дискретностью вещества и энергии.

На квантово-механическом уровне предельные точности определяются принципом неопределенности Гейзенберга, а на молекулярном уровне – законами термодинамики.

Неопределенность, предписываемая эти принципам, не присуща объектам и процессам микромира, а является следствием исходных предпосылок расчета и особенностей использованного математического аппарата.

Имеются два варианта этого аппарата – волновая механика Шредингера и матричная (квантовая) механика Гейзенберга, дающие идентичные результаты. В обоих случаях исходной предпосылкой расчета является представление о корпускулярно-волновом дуализме. Он не следует из расчета, как иногда думают, а априорно кладется в его основу – путем наделения функции волнового уравнения корпускулярными характеристиками в первом случае и введения волновых характеристик в соотношения механики – во втором.

Основным теоретическим инструментом квантовой механики является равнение Шрёдингера. В квантовой механике уравнение Шрёдингера играет такую же роль, как уравнение движения (второй закон Ньютона) в механике классической.

Уравнение Шрёдингера записывается для так называемой ψ - функции (пси - функции). В общем случае пси - функция – это функция координат и времени: ψ= ψ (x,y,z,t). Если микрочастица находится в стационарном состоянии, то пси - функция не зависит от времени: ψ = ψ (x,y,z).

В простейшем случае одномерного движения микрочастицы (например, только по оси x-икс) уравнение Шрёдингера имеет вид:

,

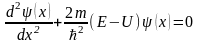где ψ(х) – пси - функция, зависящая только от одной координаты х;

m – масса частицы;

ħ - постоянная Планка (ħ = h/2π );

Е – полная энергия частицы;

U – потенциальная энергия.

В классической физике величина (Е-U) равнялась бы кинетической энергии частицы. В квантовой механике вследствие соотношения неопределенностей понятие кинетической энергии лишено смысла. Потенциальная энергия U – это характеристика внешнего силового поля, в котором движется частица. Это величина вполне определенная. Она также является функцией координат, в данном случае U=U(x,y,z).

В трехмерном случае, когда U=U(x,y,z), вместо первого

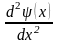слагаемого в уравнении Шрёдингера следует записать сумму трех частных производных от пси-функции по трем координатам.

Рис. 2. 3. Частные производные от пси-функции в системе координат

Если решить уравнение Шрёдингера для конкретной микрочастицы, то мы получим значение пси-функции в любой точке пространства, в котором движется частица. Это дает вероятность обнаружения частицы в той или иной области пространства равную 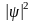. Возьмем некоторую точку в пространстве с координатами x,y,z (рис. 2.3). Зададим вопрос: какова вероятность обнаружения частицы в этой точке? Ответ: равна нулю, т. е. точка не имеет размеров, попасть в точку частица просто физически не может. Значит, вопрос поставлен некорректно. Поставим его иначе: какова вероятность обнаружить частицу в малой области пространства объемом с центром в выбранной точке? Ответ: dV = dx dy dz.

dP = ψ²(x, y, z)dV

где dP – элементарная вероятность обнаружить частицу в элементарном объеме dV.

Это уравнение справедливо для действительной пси-функции (она может быть и комплексной, в этом случае в наше уравнение надо подставлять квадрат модуля пси-функции). Если область пространства имеет конечный объем V, то вероятность P обнаружить частицу в этом объеме находится интегрированием последнего выражения по объему V:

Р =

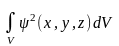
Вероятностное описание движения микрочастиц - основная идея квантовой механики. Таким образом, с помощью уравнения Шрёдингера решается основная задача квантовой механики: описание движения исследуемого объекта, в данном случае квантово-механической частицы.

Уравнение Шрёдингера является дифференциальным уравнением второго порядка. Следовательно, в процессе его решения появятся две произвольные постоянные. Для того, чтобы их найти используют так называемые граничные условия: из конкретного содержания физической задачи должно быть известно значение пси-функции на границах области движения микрочастицы. Кроме того, используется так называемое условие нормировки, которому должна удовлетворять пси-функция:

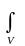ψ²(x, y, z)dV = 1

Смысл этого условия прост: вероятность обнаружить частицу хоть где-нибудь внутри области ее движения есть достоверное событие, вероятность которого равна единице.

Именно граничные условия наполняют решение уравнения Шрёдингера физическим смыслом. Без этих условий решение уравнения есть чисто математическая задача, лишенная физического смысла. В следующем разделе на конкретном примере рассмотрено применение граничных условий и условия нормировки при решении уравнения Шрёдингера.

Рассмотрим это на примере волновой механики. Исходно предполагают, что частицам присущ корпускулярно-волновой дуализм. Характеристику волн, присущих частицам, определяют из опытов по их дифракции (например, дифракции электронов).

Этот подход дал химии аппарат для расчета структур атомов, а физике – теоретические основы ядерных и корпускулярных взаимодействий, способы расчета энергетических уровней атомов и ядер и величин квантов излучаемой и поглощаемой ими энергии. Но смещение двух, хотя и взаимосвязанных, но качественно различных явлений – распространения волн и перемещения частиц – при не полном определении первого из них, с неизбежностью предопределяют неполноту квантово-механического описания, что понял и описал А. Эйнштейн. Вследствие этого, можно сформулировать принцип неопределенности Гейзенберга, который заключается в следующем – невозможно одновременно точно измерить координаты (x, y, z) и импульсы (P_x, P_y, P_z) частицы.

Этот принцип справедлив на квантомеханическом уровне.

Принцип неопределенности Найквиста может быть описан неравенством, которое представляет собой ограничение, накладываемое на точность измерения на молекулярном уровне:

γ²ηPt ≥ W_ш,

где Pt – энергия измеряемого сигнала;

W_ш, - энергия шума;

γ – относительная точность;

η – КПД;

t - время измерения.

В техническом смысле эти принципы приводят к следующему. Принцип технологического несовершенства приборов состоит в том, что невозможно создать измерительный прибор, характеристики которого точно соответствовали бы проектным характеристикам из-за несовершенства технологического процесса изготовления прибора и его элементов.

Технологические несовершенства характеризуются совокупностью таких параметров, как неточность изготовления деталей и элементов, настройка и регулировка прибора, выдерживание режимов тепловой обработки (закалки, отжига и т. д.), обработки поверхностей. Принцип воздействия внешних возмущений на прибор заключается в том, что сигналы в приборе подвергаются внешним возмущениям (электромагнитных и гравитационных полей, полей ускорения и вибраций и др.), приводящие к появлению ошибок при измерении.

Принцип несовершенства технологии измерения заключается в том, что любое измерение при идеальном приборе не может быть абсолютно точным, так как сама схема технологии измерения несовершенна (неточность снятия показаний, и установки прибора, конечное время произведения измерения, непостоянство внешних условий и т. д.).

Вышеприведенные принципы указывают на наличие предельных ограничений, накладываемых природой и уровнем развития техники на точность измерений, и показывают принципиальную невозможность полного устранения неопределенности результатов измерений.

2.4. Принципы построения измерительных систем.

Применение и развитие измерительной техники всегда было обусловлено потребностями производства, торговли и других сфер человеческой деятельности.

Контрольно-измерительные операции давно стали неотъемлемой частью технологических процессов и в значительной степени определяют качество выпускаемой продукции. Прогресс измерительной техники неразрывно связан с научно-техническим прогрессом.

Новые научные и технические задачи приводят и к новым измерительным задачам, для решения которых нужны новые средства измерений (СИ), а новые научные и технические результаты влияют на уровень измерительной техники:

- повышается точность измерений, и расширяются диапазоны измерения;

- растет номенклатура измеряемых величин;

- увеличивается производительность измерительных операций, и за счет их автоматизации уменьшается влияние человеческого фактора;

- возрастает число выполняемых функций.

Информационные измерительные системы (ИИС) являются симбиозом аппаратных средств и алгоритмов обработки измерительной информации. Поэтому как проектирование ИИС, так и их применение невозможны без правильного теоретического обоснования и понимания этих алгоритмов.

При этом, благодаря наличию в составе ИИС ЭВМ, возможна дальнейшая обработка результатов измерений, полученных путем обработки первичной измерительной информации. Это позволяет решать с помощью ИИС широкий спектр других задач, не являющихся чисто измерительными, в частности контроль качества, распознавание образов и др.

Классификация ИИС.

Классификация различных изделий производится с целью выявления общих моментов в функционировании, конструировании и эксплуатации уже имеющихся видов изделий, что может оказаться полезным при создании новых видов однотипной продукции, указывая возможные направления решения поставленной задачи. Классификация может производиться по различным классификационным признакам, отражающим различные свойства классифицируемых изделий.

Это приводит к появлению различных групп классов для изделий одного вида. При этом следует иметь в виду, что всякая классификация условна и ее содержание может меняться по мере изменения свойств классифицируемых изделий, в частности в результате изменения используемых при их изготовлении материалов, комплектующих и технологий.

Это относится и к классификации ИИС, и к другим видам классификации, с которыми мы встретимся ниже.

Классификация ИИС производится в соответствии с различными классификационными признаками, отражающими область применения, функции и конструкцию ИИС:

- функциональное назначение;

- вид и характер входных величин;

- вид выходной информации;

- вид структурно-функциональной схемы ИИС;

- принцип построения.

Первый классификационный признак нам представляется наиболее важным. Он в первую очередь интересует потребителя (пользователя) ИИС. Этот признак не зависит от технических средств реализации ИИС. Не случайно, что этот вид классификации не менялся и не встречал возражений за более чем полувековую историю существования ИИС.

Целью функционирования всех сложных технических систем является либо исследование физических явлений, либо управление технологическим процессом. В последнем случае одной из функций всегда является определение значений физических величин, являющихся непременной частью любого технологического процесса.

Таким образом, необходимой составляющей функционирования всех без исключения сложных технических систем является определение состава параметров физических процессов, которые эти системы должны обслуживать, их измерение, анализ полученных результатов и принятие на их основе определенных решений. Последняя функция в основном относится к управляющим системам.

Однако в силу высокого уровня развития современных ИИС эти задачи могут решаться и ими.

С учетом этого в зависимости от функционального назначения, то есть в зависимости от вида решаемых задач, ИИС подразделяются на следующие классы:

- измерительные системы;

- статистические измерительные системы;

- системы автоматического контроля;

- системы технической диагностики;

- системы распознавания образов;

- системы идентификации.

Иногда выделяется еще один класс выявления (обнаружения) событий. Однако этот класс столь неопределенен с точки зрения формулировки решаемой задачи (например, выявление неопознанных летающих объектов или установление факта телепатической связи), что, не отрицая возможности постановки таких задач, трудно найти общие черты в методах их решения.

Эта общепринятая классификация является четкой по отношению к виду решаемых задач.

Однако с терминологической и конструктивной точек зрения можно сделать два замечания.

Во-первых, выделение класса измерительных систем из измерительных информационных систем содержит некоторую тавтологию, особенно, если вспомнить, что в настоящее время в терминологических документах ИИС трактуется как подкласс измерительных систем.

Во-вторых, измерительные системы в подавляющем большинстве случаев составляют основу всех других систем, будучи дополнены соответствующими алгоритмами обработки измерительной информации. При этом важно подчеркнуть, что структура всех классов ИИС оказывается одинаковой.

Терминологически было бы более правильным говорить об ИИС, предназначенных для решения только измерительных задач. Однако стилистически такой оборот не совсем удобен.

Другие классификационные признаки нам представляются менее существенными, прежде всего потому, что их содержательная сторона быстро изменяется с изменением используемых технических средств. Вид входных величин определяется физическими свойствами исследуемого объекта (ИО). Если эти величины одинаковы по физической природе, то классификация по этому признаку информативна. Например, при измерении размеров детали используются ИС для пространственных или геометрических измерений, при контроле напряжений в механических элементах машин используются механические ИС, для контроля энергопотребления в электросети применяются ИС для измерения электрических величин.

Однако очень часто входные величины бывают различными по физической природе. С такими ситуациями сталкиваются при исследовании свойств материалов, при контроле окружающей среды и влияющих на нее факторов и др. Очевидно, что если величины разнородны, то этот признак классификации нецелесообразен.

Характер входных величин (независимо от их физической природы) отражается в следующих признаках:

- количество величин;

- поведение во времени: неизменное или изменяющееся;

- расположение в пространстве: сосредоточенное или распределенное;

- представление величин: дискретное или непрерывное;

- энергетический признак: активность, пассивность;

- характер помех, суммирующихся с величиной: независимые помехи; помехи, зависимые от исследуемых величин.

Остальные признаки связаны в основном с конструкцией ИС и слабо влияют на их функциональное назначение.

Классификация по видам выходной информации включает в себя следующие классы:

- характер выходной информации: измерительная информация (именованные числа, их отношения, графики и т. п.), количественные суждения (выводы по результатам контроля, диагностики, идентификации);

- степень обработки выходной информации: результаты оценки одного показателя; показатели, характеризующие функциональные зависимости; статистические показатели;

- потребитель информации: человек-оператор, ЭВМ, АСУ.

Различают следующие виды структурных схем ИС:

- последовательного действия (одноканальная система);

- параллельного действия (многоканальная система);

- параллельно-последовательного действия (с коммутатором на входе);

- мультиплицированная структура.

При классификации по принципам построения используются следующие признаки:

- наличие специального канала связи;

- унификация состава системы;

- порядок выполнения операций: последовательный или параллельный;

- наличие или отсутствие структурной и информационной избыточности;

- наличие или отсутствие адаптации, характер адаптации;

- наличие или отсутствие информационной обратной связи;

- вид используемых сигналов: аналоговые или кодоимпульсные;

- наличие стандартного интерфейса.

В качестве отдельного класса рассматриваются телеметрические системы. По своим функциям они могут относиться к любому из перечисленных выше классов. Специфика этих систем заключается в том, что они предназначены для телеизмерений - измерений на расстоянии и, следовательно, имеют более протяженные каналы связи, чем другие ИС.

Описанная система классификации используется довольно широко. Однако ее значение в основном терминологическое, поскольку система проектируется исходя из решаемых задач и технико-экономических ограничений, а затем полученные результаты могут быть отнесены к конкретному классу. Практическая эффективность этой классификации невелика.

Общие принципы построения и применения ИС.

Создаваемая ИС должна обеспечивать достижение поставленных перед ней целей. Эти цели могут быть достигнуты различными способами. Поэтому должны быть определены критерии сравнения различных вариантов - количественные показатели качества ИС. Эти показатели, как и для всех сложных устройств и систем, имеют многоплановый характер.

Основным показателем качества ИС как СИ, отражающим ее назначение и специфику конкретного применения, является показатель достоверности выдаваемой информации.

Для измерительных систем (включая статистические) показателем достоверности, как и для всех СИ, является погрешность измерения или неопределенность результата измерений.

Для систем контроля и систем распознавания образов достоверность принимаемых решений характеризуется вероятностями ошибок. Более сложна оценка достоверности результатов, выдаваемых системами технической диагностики и системами идентификации. Однако она тоже сводится к некоторым вероятностным характеристикам.

Свойства ИС как информационной системы характеризуются количеством выдаваемой информации, скоростью выдачи и информационной избыточностью. Эти показатели могут непосредственно интересовать потребителя.

Следует отметить, что возможности современной вычислительной техники и каналов передачи информации таковы, что во многих случаях обеспечение требуемых информационных характеристик достигается без особых усилий.

Измерительная система характеризуется также общетехническими показателями: габариты, масса, потребляемая мощность, показатели безопасности, надежность и др.

Определенной спецификой среди этих показателей обладает надежность, так как она определяется не только надежностью технических средств и общей структурой ИИС, но зависит и от свойств программно-математического обеспечения.

При разработке и применении ИИС не следует упускать из виду экономические аспекты. При этом с экономической точки зрения необходимо учитывать два противоречивых момента.

Измерительные системы в силу своей сложности являются более дорогим средством измерения. В то же время ее применение может значительно повысить производительность и достоверность контрольно-измерительных операций, что приведет к повышению качества выпускаемой продукции, то есть принести значительный экономический эффект.

Кроме того, гибкость ИИС позволяет с ее помощью заменить несколько традиционных СИ, что также увеличивает экономический эффект от ее применения. Эти факторы доступны достаточно точному экономическому анализу.

При проектировании ИИС, как и систем любого другого вида, необходимо руководствоваться системотехническим подходом. При этом следует иметь в виду, что ИС представляет собой некоторую иерархическую структуру, верхним уровнем которой является вычислительное устройство, а нижним - первичные измерительные преобразователи, контактирующие с ИО. При наличии обратной связи передача информации происходит не только от нижних уровней к верхним, но и в обратном направлении.

На промежуточных уровнях также могут находиться микропроцессорные вычислительные устройства. Иерархичность многовходовых (многоканальных) ИС очевидна, но даже простейшие одноканальные ИС имеют структуру, которую можно считать иерархической.

При этом следует различать два вида иерархических структур:

- функциональную структуру (датчики, вторичные преобразователи, каналы связи, центральная ЭВМ);

- конструктивную структуру (система, блок, плата, элемент).

Благодаря миниатюризации компонентов электронной и вычислительной техники структура второго вида постоянно упрощается при сохранении функциональной структуры.

Организация структуры сложных технических систем должна исходить из нескольких общих принципов.

Принцип сочетания системности и агрегирования.

Этот принцип является основным в создании систем и предполагает обязательный учет двух факторов.

Во-первых, система рассматривается как единое целое со своими функциональными, информационными и конструктивными связями и показателями.

Во-вторых, образующие систему элементы, сохраняя определенную автономность и заменяемость, должны быть совместимы: конструктивно, информационно (уровни входных и выходных сигналов, интерфейсы), по характеристикам питания, условиям эксплуатации и т. д.

Принцип однородности иерархического уровня.

На одном иерархическом уровне не должны присутствовать устройства, принадлежащие другому иерархическому уровню.

Например, в одном функциональном уровне не должны сосуществовать первичные и вторичные преобразователи, хотя конструктивно устройства младшего иерархического уровня могут быть размещены в устройствах соответствующего старшего уровня.

Обеспечение этого принципа позволит четко определить функциональную принадлежность каждого устройства.

Принцип максимальной функциональной замкнутости.

Этот принцип предполагает создание такой иерархической структуры, при которой любое более крупное (старшее) объединение делится на более мелкие (младшие) объединения по функциональному признаку.

Принцип максимальной функциональной замкнутости предполагает, что каждое структурное объединение способно функционировать без привлечения каких-либо структур, размещенных в других структурных объединениях. Для выполнения важных, но вспомогательных функций, например, для обеспечения электропитания, могут привлекаться элементы других уровней.

Необходимость обеспечения максимальной функциональной замкнутости выдвигает два следующих правила отнесения младших структурных объединений к старшим:

1) каждое старшее структурное объединение должно включать в свой состав те младшие структуры, функционирование которых при невозможности их полной автономии обеспечивается другими младшими структурными объединениями, принадлежащими этому старшему структурному объединению.

2) каждое старшее структурное объединение должно включать в свой состав те младшие структурные объединения, которые обеспечивают функционирование этого старшего объединения.

Принцип минимизации старших иерархических информационных связей.

Отработка всякой системы тем сложнее и тем длительнее, чем больше устройств нужно сопрячь для совместной работы.

Представляет трудность отработка каждой функции, которая должна решаться несколькими устройствами совместно.

Поскольку количество таких функций обычно прямо пропорционально объему информации, которой обмениваются эти устройства, то следует стремиться к сокращению этого объема, тем самым сокращая и число совместно реализуемых функций.

Принцип наращиваемости аппаратуры.

Этот принцип заключается в возможности добавления или, наоборот, съема части аппаратуры системы без каких-либо изменений в оставшейся части.

Выполнение этого принципа оказывается крайне полезным как в условиях эксплуатации, так и при наращивании функций измерительных систем. Реализацией этого принципа, наряду с возможностью наращивания программно-математического обеспечения, обеспечивается гибкость измерительных систем в части выполняемых функций.

Принцип наращиваемости аппаратуры предполагает использование таких технических решений, которые позволят изменять состав аппаратуры в большую или меньшую сторону без какого бы то ни было изменения любых звеньев ИС.

Принцип физической однородности распределения функций.

Непосредственно измеренная датчиками первичная информация о физических величинах не всегда пригодна для непосредственной математической обработки совместно с результатами измерения других величин.

Первичная информация должна пройти предварительную первичную обработку - фильтрацию, усреднение, совместную математическую обработку с другими однородными физическими величинами и т. п. Развитие вычислительной техники и возможность применения малогабаритных вычислителей относительно небольшой мощности позволяют разделить всю математическую обработку на первичную и вторичную. Первичную обработку могут выполнять микропроцессорные устройства, объединенные с первичными или вторичными преобразователями (интеллектуальные датчики), а вторичную - центральная ЭВМ.

Рассмотренные принципы справедливы не только для структуры системы в целом, но и для структуры каждой подсистемы, входящей в ее состав, и вообще для каждого звена любого уровня, включая элементы. Следование этим принципам обеспечивает повышение надежности, взаимозаменяемость устройств, упрощает отработку каждого функционального узла.

Можно выделить основные этапы создания информационных систем (ИС).

1. Выбор физической и математической моделей исследуемого объекта и формирование на их основе цели ИС с учетом ее функций в технологическом или исследовательском процессе. На этом этапе ведущая роль принадлежит заказчику (пользователю).

При этом возможно проведение совместных предпроектных работ с целью уточнения окончательного вида моделей.

2. Разработка алгоритмов сбора и первичной обработки измерительной информации, разработка структуры ИС и выбор технических средств с учетом их комплексирования и системной совместимости (информационной, конструктивной, энергетической, метрологической, эксплуатационной и т. п.). Задачи этого этапа решаются разработчиком ИС.

3. Разработка программно-математического обеспечения (ПМО).

4. Разработка метрологического обеспечения ИС, включающего в себя методы оценки неопределенности получаемых результатов и методику поверки или калибровки.

Задачи каждого этапа могут быть решены только при совместной работе заказчика (пользователя) ИС и разработчика.

Особенно велик удельный вес работ заказчика на первом этапе, поскольку только он может определить, какие физические величины используются для описания ИО, какие используются при этом физические и математические модели и что является целью функционирования ИС (целью измерения или целью обработки полученных результатов).

На последующих этапах основная роль принадлежит разработчику, однако и на этих этапах необходимо учитывать мнение заказчика, в первую очередь в части эргономических свойств ИС.

Современные ИС обладают большой гибкостью, когда на базе одних и тех же аппаратных средств (измерительных каналов и средств вычислительной техники) можно решать различные измерительные задачи, часть которых могла не ставиться на начальном этапе разработки ИС. Эта специфика ИС должна учитываться при их проектировании. В частности, должна предусматриваться возможность подключения новых измерительных каналов, а возможно, и разработка этих каналов.

Контрольные вопросы

1. Что такое физическая величина?

2. Что такое размерность и формула размерности?

3. В чем заключается функциональная внутренняя структура измерительной системы?

4. Что такое эффекты переноса?

5. Чем отличаются активный и пассивный датчики?

6. В чем смысл принципов неопределенности и дополнительности?

7. В чем заключается принцип неопределенности Гейзенберга?

8. В чем заключается принцип неопределенности Найквиста?

9. В чем заключается принцип технологического несовершенства приборов?

10. В чем заключается принцип несовершенства технологии измерения?

11. В чем заключаются принципы построения измерительных систем?

12. Как классифицируются измерительные системы (ИС)?

13. Каковы этапы создания измерительных систем?

14. В чем заключается принцип сочетания системности и агрегирования ИС?

15. В чем заключается принцип однородности иерархического уровня ИС?

16. В чем заключается принцип максимальной функциональной замкнутости ИС?

17. В чем заключается принцип наращиваемости аппаратуры ИС?

18. Каков смысл принципа физической однородности распределения функций ИС?

19. В чем заключены общие принципы построения и применения измерительных систем?

20. Чем характеризуется измерительная система?