Анализ размерностей. Рассмотрим анализ размерностей на примере математического маятника (рис. 1. 29).

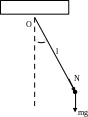
Рис. 1. 29. Схема математического маятника

Математический маятник − это материальная точка, закрепленная на нерастяжимой невесомой нити, совершающая колебания под действием силы тяжести относительно положения равновесия.

Начальные условия:

a₁=m − масса материальной точки,

a₂=l − длина нити, закрепленной в точке О,

a₃= t −время колебания,

a₄=g − ускорение свободного падения g = 9,8 м/c²,

a= − угол между нитью и вертикалью.

Определим закон движения маятника, отклоненного в начальный момент на угол ₀ = a₅ и отпущенного из этого положения с нулевой угловой скоростью. Закон движения нити l будет функцией пяти аргументов:

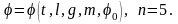
Определим размерности каждого аргумента:

[a₁]= [m] = М, [a₂]=[l]= L, [a₃]= [t] = T ,

[a₄]= [g] = LT^-2, [a₅]= [₀] = 1.

Величина  тоже безразмерная, т. е. [] = 1.

Следовательно, только три величины t, l, m, имеют независимые размерности (k = 3).

Если воспользоваться П-теоремой, то закон движения можно записать в виде функции от n-k=2 безразмерных аргументов.

Найдем эти аргументы:

, .

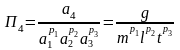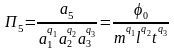Для определяемой величины:

.

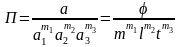Размерности числителей и знаменателей в этих формулах должны совпадать, поэтому показатели знаменателей находятся однозначно:

[g]= LT^-2=[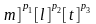 = =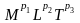> p₁=0, p₂=1, p₃= −2;

[₀] = 1=[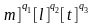 = =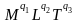> q₁=0, q₂=0, q₃= 0; m₁=0, m₂=0, m₃=0.

Получаем две возможные безразмерные комбинации: П₄= , П₅=₀.

Для искомого значения: П=.

В результате зависимость запишется в виде:

П=(1,1,1, ,₀)= ( ,₀) или =( ,₀).

Таким образом, мы получили важный вывод: закон движения маятника не зависит от массы груза.

Анализ размерностей — метод, используемый физиками для построения обоснованных гипотез о взаимосвязи различных размерных параметров сложной физической системы.

Иногда анализ размерности можно использовать для получения готовых формул (с точностью до безразмерной константы).

Суть метода заключается в том, что из параметров, характеризующих систему, составляется выражение, имеющее нужную размерность.

В основе анализа размерностей лежит требование равенства размерностей в левой и правой частях уравнения.

Формула размерности физической величины имеет вид:

[N] = L^l M ^mT ^t.,

где [N] — символ размерности вторичной величины;

L, М, Т, . — символы величин, принятых за основные (соответственно длины, массы, времени и т. д.);

l, m, t, . — целые или дробные, положительные или отрицательные вещественные числа.

Если для исследуемого явления установлено, с какими величинами может быть связана искомая величина, но вид этой связи неизвестен, то можно составить уравнение размерностей, в котором в левой части будет стоять символ искомой величины со своим показателем размерности, а в правой — произведение символов величин, от которых искомая величина зависит, но с неизвестными показателями размерности.

Задача нахождения связи между физическими величинами сводится в этом случае к отысканию значений соответствующих показателей размерности.

Пример. Требуется определить время t прохождения пути l телом массой m, движущимся поступательно и прямолинейно под действием постоянной силы f, т. е. время t зависит от l, m, f: t=t(l,m,f). Но в любой системе единиц имеется несколько основных единиц, а все остальные через основные единицы выражаются.

Так, в системе СИ, единицы времени, массы и длины основные, а единица силы выражается через них:

F=MLT^-2.

Такое выражение единицы (любой физической величины - ФВ) в определенной системе единиц называется размерностью данной ФВ.

Поскольку в равенстве t = t(l, m, f) справа и слева должны стоять величины одинаковой размерности, то получаем формулу:

t = C·l^x ·my·f·z,

где С −некоторая безразмерная постоянная;

x,y,z − неизвестные числа, которые следует определить.

Поскольку С − безразмерна, то формуле t = Cl^xm^yf^z соответствует следующее равенство размерностей:

Т = Lx·My (MLT^—2) ^z,

Это равенство должно выполняться тождественно, не зависимо от того каковы численные значения l, m и f. Поэтому следует приравнять показатели степени при L, M и T:

L : x + z = 0, M : y + z = 0, T : −2z = 1,

откуда следует, что х = у = ¹/₂, z = −¹/₂ .

Поэтому формула t=C·l^x ·m^y ·f^z примет вид: t = C .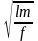

Так как, безразмерный коэффициент С, равный, согласно законам механики 1, то в рамках анализа размерностей его определить нельзя.

В этом состоит своеобразие анализа размерностей Устанавливаемая с его помощью зависимость искомой величины от величин, определяющих исследуемое явление, находится с точностью до постоянного коэффициента (или коэффициента, зависящего от безразмерного параметра, например от угла). Для получения точных количественных соотношений нужны дополнительные данные. Поэтому анализ размерностей не является универсальным методом. Он нашёл плодотворное применение в тех областях физики (гидравлике, аэродинамике и др.), где строгое решение задачи часто наталкивается на значительные трудности, в частности из-за большого числа параметров, определяющих физические явления. При решении на основе анализа размерностей сложных задач большую роль сыграла П-теорема. Эта теорема связывает анализ размерностей с теорией физического подобия, в основе которой лежит утверждение, что если все соответствующие безразмерные характеристики (критерии подобия) для двух явлений одинаковы, то эти явления являются физическими.

Установление искомых закономерностей с помощью физического моделирования зачастую является единственно возможным способом экспериментального изучения и решения важных и нужных практических задач. Так обстоит дело при изучении природных явлений, где процессы бывают необычайно сложны и протекают в течение десятков, сотен или даже тысяч лет. В условиях модельных опытов подобное явление может продолжаться всего несколько часов или дней. С этим мы встречаемся при моделировании явлений просачивания нефти, разрабатываемой и откачиваемой через скважины, таяния и сползания ледников и др. Могут быть и обратные случаи, когда вместо исследования, очень быстро протекающего в природе явления, можно экспериментально изучать подобное ему явление, происходящее на модели гораздо медленнее.

Моделирование с успехом применяется в разработке новых типов самолетов, космической техники, создании ядерного оружия, кораблестроении, автомобилестроении, биомеханике, океанологии, метеорологии, астрофизике, науке о Земле и планетах и во многих других областях человеческой деятельности.

Физическое моделирование — ответственная научная задача, имеющая общее принципиальное и познавательное значение. Оно основывается на глубоком проникновении в явление (в процесс), в разработку экспериментальных и теоретических методов исследования для получения достоверных результатов и в итоге получения систематических правил и рекомендаций для решения конкретных практических задач.

Альтернативой физическому моделированию является математическое моделирование, приведшее в последние десятилетия ХХ века к подлинно революционному преобразованию науки вообще и математики в особенности и гармонично дополняющее физическое моделирование.

Математическое моделирование — это, как правило, численное решение на ЭВМ алгебраических, дифференциальных или интегральных уравнений, вытекающих из применения законов механики, физики, химии, биологии, экономики к решению конкретных задач.

Теория размерности и подобия имеет большое значение при моделировании различных явлений.

Моделирование - это есть замена изучения интересующего нас явления в натуре изучением аналогичного явления на модели меньшего или большего масштаба, обычно в специальных лабораторных условиях. Основной смысл мо­делирования заключается в том, чтобы по результатам опытов с моделями можно было давать необходимые ответы о характере эффектов и о различных величинах, связанных с явлением, в натурных условиях.

Часто моделирование основано на рассмотрении физически подобных явлений. Изучение интересующего нас натурного явления мы заменяем изучением физически подобного явления, которое удобнее и выгоднее осуществить. Для правильного физического моделирования необходимо:

1. Установить условия подобия двух явлений − в модели и натуре.

2. Определить, как ими пользоваться для проектирования натурных объектов с заданными параметрами или предсказания явлений натурных процессов.

Физическое подобие можно рассматривать как обобщение геометрического подобия. Две геометрические фигуры подобны, если отношения всех соответственных длин одинаковы, а углы при соответствующих вершинах — для обеих фигур равны.

Существуют различные способы определения механического или физического подобия. Ниже мы даем определение физического подобия в такой форме, которая необходима для практики и удобна для непосредственных приложений.

Два явления подобны, если по заданным характеристикам одного можно получить характеристики другого простым пересчетом, который аналогичен переходу от одной системы единиц измерения к другой системе.

Для физического подобия двух геометрически подобных явлений необходимо и достаточно, чтобы они определялись одним и тем же набором определяющих параметров а₁, a₂,..., a_n численные значения которых могут отличаться в этих явлениях, но при этом, численные значения безразмерных параметров П_k+1,..., П_n совпадают в этих явлениях. В связи с принятым определением подобных явлений параметры П_k+1,..., П_n называются параметрами подобия.

При подобии двух явлений, которые мы будем далее называть одно натурным и другое модельным, определяемая величина «а» должна иметь одинаковую функциональную зависимость от определяющих параметров

,

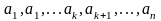Для натурного явления

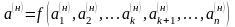
Для модельного явления

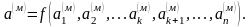
Здесь верхние индексы (н) и (м) относятся соответственно к натуре и модели.

Применяя П-теорему, обе зависимости перепишем в безразмерном виде

П^(н)=f (1,…,1,П^(н)_k+1,..., П^(н)_n),

П^(м)=f (1,…,1,П^(м)_k+1,..., П^(м)_n), (1)

Если условия подобия выполнены, то должны выполняться равенства

П^(н)_k+1= П^(м)_k+1,…, П^(н)_n= П^(м)_n , (2)

Эти условия называют критериями подобия. Следовательно, получаем равенство безразмерной определяемой величины для модели и натуры

П^(н) = П^(м) , (3)

Возвращаясь от равенства (3) обратно к размерным переменным 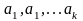, получим простое правило пересчета результатов измерений с подобного модельного явления на натурное явление в виде:

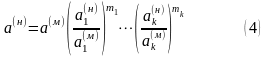
Все, что стоит справа в (4) после a^(м), часто называют переходным масштабом. Для k величин с независимыми размерностями переходные масштабы могут быть произвольными, и их нужно задавать или определять условиями задачи, а при экспериментах — из опытов, имея в виду получение максимальной простоты и удобство моделирования.

Переходные масштабы для всех же остальных размерных величин 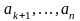для обеспечения подобия модели натуре получаются из условия (3):

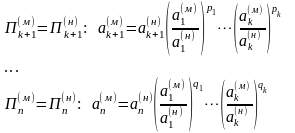
Приведенные выше простые определения и утверждения полностью исчерпывают содержание теории подобия. Однако на практике часто выполнение всех условий одновременно бывает затруднено и тогда встает вопрос о величине погрешностей (масштабном эффекте), которые возникают при переносе на натуру результатов, полученных на модели.

Здесь возникает проблема приближенного моделирования (иногда часть безразмерных параметров слабо влияет на результат, тогда выполнение некоторых критериев (3) можно игнорировать, иногда прибегают к частичному или локальному моделированию, условия для которого ослаблены по сравнению с условиями полного моделирования (3).

Контрольные вопросы:

1. Каковы основные принципы построения механистической картины мира?

2. Каковы основные черты электромагнитной картины мира?

3. Каковы результаты применения теории отражения?

4. С какой целью применяют П-теорему?

5. Какое значение имеет теория размерностей и подобия?

6. Что такое адиабатические инварианты?

7. В чем заключается корпускулярно-волновой дуализм?

8. В чем смысл самоорганизации материи?

9. Почему в современной картине мира основным материальным объектом является вездесущее квантовое поле?

10. Что такое гравитоны и фотоны ?

11. Какие константы относятся к макромиру, а какие к - микромиру?

12. Как был определен эталон в 1 метр длины?

13. Как был определен эталон в 1 секунду времени?

14. Как были определены эталоны в 1 градус температуры?

15. Каковы основные принципы теории относительности?

16. Что устанавливает квантовая механика?

17. Почему для реализации стандартов длины использова-лись лазеры?

18. В чем заключается реализация единицы массы, времени, температуры, силы света, силы электрического тока?

19. В чем заключается классификация хроматографии?

20. Что такое кандела?

21. Что такое сингулярность?