Погрешности исходных данных учитывают по формуле

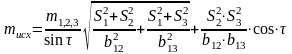, (2.39)

где m₁ = m₂ = m₃ = m_1,2,3 – погрешности в положении исходного пункта;

 = ₁ + ₂ + ₂₁₃ – 180.

Например, при S_ср  1350 м, b_ср  2200 м, ₂₁₃  80, m_ =2, m_1,2,3 = 5 мм получим m_с.з. = 11,5 мм, m_и = 6,2 мм, а общая погрешность вынесения на местность проектной точки способом обратной угловой засечки составит

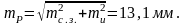
Способ линейной засечки

В способе линейной засечки положение выносимой в натуру точки С (см. рис. 2.7) определяют в пересечении проектных расстояний S₁ и S₂, отложенных от исходных точек А и В. Этот способ обычно применяют для разбивки осей строительных конструкций в случае, когда проектные расстояния не превышают длины мерного прибора.

Наиболее удобно разбивку производить при помощи двух рулеток. От точки А по рулетке откладывают расстояние S₁, а от точки В по второй рулетке — S₂. Перемещая обе рулетки при совмещенных нулях с центрами пунктов А и В, на пересечении концов отрезков S₁ и S₂ находят положение определяемой точки С.

Средняя квадратическая погрешность в положении определяемой точки в общем виде выражается формулой, аналогичной выражению (2.34) для угловой засечки. Погрешность собственно линейной засечки может быть подсчитана по формуле

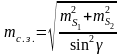(2.40)

Минимальной погрешность собственно линейной засечки будет при =90°. В этом случае

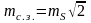(2.41)

Влияние погрешностей исходных данных в линейной засечке выражается формулой

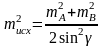. (2.42)

Для засечки при  = 90° m_исх = m_AB.

В случае применения мерных приборов погрешности центрирования отсутствуют. Тогда общая погрешность в определении положения разбиваемой точки С будет в основном зависеть от суммарной погрешности собственно засечки и исходных данных и выражаться формулой

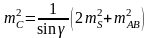. (2.43)

Для приближенных расчетов, приняв  = 90°, будем иметь

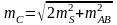(2.44)

Определить необходимую точность отложения разбивочных расстояний можно, если задана точность определения проектного положения выносимой в натуру точки и известна погрешность в положении исходных пунктов [3,6]. Так, например, при m_C = 10 мм и m_AB = 5 мм из формулы (2.44) можно получить

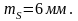
В случае, если для линейной засечки применяются дальномерные комплекты, которые центрируются при помощи штативов, то влияние погрешностей центрирования можно определить по формуле

. (2.45)

Способ полярных координат

Способ полярных координат широко применяют при разбивке осей зданий, сооружений и конструкций с пунктов теодолитных или полигонометрических ходов, когда эти пункты расположены срав­нительно недалеко от выносимых в натуру точек.

В этом способе положение определяемой точки С (рис. 2.9) находят на местности путем отложения от направления АВ проектного угла  и расстояния S. Проектный угол  находится как разность дирекционных углов _АВ и _АС , вычисленных как и расстояние S из решения обратных геодезических задач по координатам точек А, В и С.

Для контроля положение зафиксированной точки С можно проверить, измерив угол на пункте В и сравнив его со значением, полученным как разность дирекционных углов _ВА и _ВС..

Р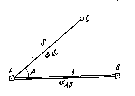 ис. 2.9. Схема разбивки способом полярных координат

Средняя квадратическая погрешность выноса в натуру точки С определяется формулой

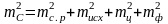(2.46)

Погрешность собственно разбивки полярным способом зависит от погрешности m_ построения угла  и погрешности m_s отложения проектного расстояния S

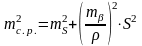. (2.47)

Влияние погрешностей исходных данных при m_А = m_B = m_АВ выражается формулой

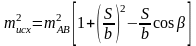, (2.48)

а погрешностей центрирования

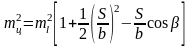(2.49)

Формулы (2.48) и (2.49) аналогичны. Из этих формул следует, что для уменьшения влияния ошибок исходных данных и центрирования необходимо, чтобы угол  и отношение 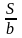были минимальны, полярный угол был бы меньше прямого, а проектное расстояние — меньше базиса разбивки, т. е. 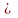 90°, S b.

Для приближенных расчетов, приняв  = 90° и S=b, получим

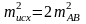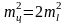; , (2.50)

а для суммарной погрешности в положении точки, разбиваемой способом полярных координат,

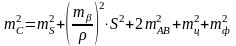. (2.51)

Для примера оценим точность разбивки проектного положения точки с пунктов полигонометрии (b = 250 м, m_AB = 10мм). Примем S =100 м, 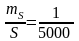, 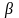= 45°, m_ = 10", 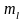= 1 мм и m_ф=1 мм.

Погрешность отложения проектной линии составит 20 мм; линейная величина погрешности построения проектного угла – 5 мм; влияние погрешностей исходных данных – 9,4 мм.

Из соотношения полученных величин видно, что погрешностями центрирования и фиксации можно пренебречь. Таким образом, погрешность разбивки, вычисленная по формуле 2.51, составит 23 мм.

Расчет показывает, что для данных условий уменьшение погрешности в положении выносимой в натуру точки возможно лишь при существенном уменьшении погрешности отложения проектного расстояния, хотя бы в два раза [6].

Е сли разбиваемая точка находится на значительном расстоянии от исходного пункта, то применяют способ проектного полигона (рис. 2.10).