Лабораторна робота №1

Застосування перетворень Фур’є в ідентифікації та моделюванні технологічних процесів

Лабораторна робота №1

Застосування перетворень Фур’є в ідентифікації та моделюванні технологічних процесів.

Мета роботи: вивчення та застосування перетворень Фур’є при рішенні задач ідентифікації.

Теоретична частина

Метод перетворення Фур'є грає винятково важливу роль у математичній фізиці. За допомогою перетворення Фур'є можна досліджувати хімічну будову віддалених планет (спектральний аналіз сигналів радіотелескопів), досліджувати функціональні системи людського організму (спектральний аналіз кардіограм, енцефалограм) і т.д.

Вираз виду:

називаються тригонометричними поліномами (ступеня π). Виявляється, що будь-яка безперервна (і не тільки безперервна) функція на проміжку (-π,π) може бути апроксимована з попередньо заданою точністю тригонометричними поліномами з відповідними коефіцієнтами a₀ ,…,a_n, та b₀ ,…, b_n.

Це твердження можна проілюструвати, порівнюючи графіки функцій y=x, y=|x|, y=x² з графіками тригонометричних поліномів, що апроксимують ці функції (рис. 1):

Цікаво помітити, що для наближення функцій y=|x| і y=x² із задовільною точністю потрібно менше гармонік, чим у випадку функції y=x.

Лінійні комбінації функцій виду і також називають тригонометричними поліномами, мають період 2πТ. Тому можна так переформулювати наше твердження: будь-яка періодична функція може бути апроксимована тригонометричними поліномами.

Цей факт, виявлений Фур'є в ході його досліджень по поширенню тепла, має важливе значення для фізики. Дійсно, функції синус і косинус описують найпростіші хвилі, названі монохроматичними, тобто хвилі фіксованої довжини (або фіксованої частоти, якщо розглядати їх як час). Оскільки будь-яку періодичну функцію можна інтерпретувати як профіль деякої хвилі, відкриття Фур'є можна виразити в такий спосіб: будь-яка хвиля може бути представлена як суперпозиція (сума) монохроматичних хвиль.

Для знаходження коефіцієнтів Фур’є використовується наступний метод. Нехай функція , що має період , представлена рядом Фур’є:

(1)

Для тригонометричних функцій виконуються відношення:

(2)

де при .

Отже, якщо формально помножити рівність (1) на або і почленно проінтегрувати від до , то зайві гармоніки зникнуть і отримаємо формулу для коефіцієнтів:

, (3)

Замітимо, що в силу формули Ейлера будь-який тригонометричний поліном може бути записаний в такому вигляді:

де

Тому формули (1) і (3) можна переписати до більш простішого вигляду (приймаючи Т=1):

(4)

Для опису дискретних розкладів є – інтегральна формула Фур’є. Її можна одержати, якщо підставити вираз (3) в формулу (1) і переходячи формально до границі Т→ ∞:

(5)

де

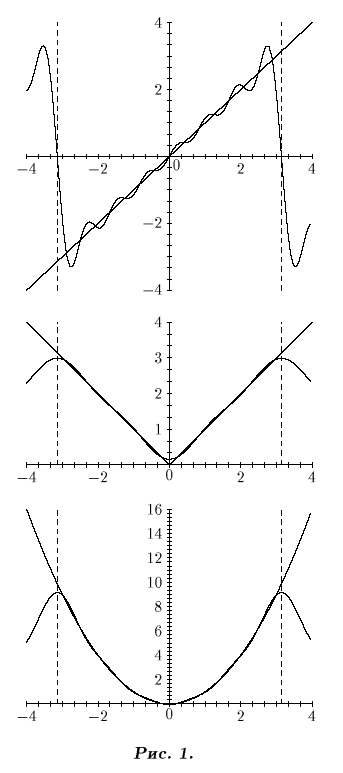
Рис.1

Теорія рядів Фур’є і безперервного перетворення Фур’є досить складна і підносить чимало несподіванок. Однак не обов’язково володіти цією теорією в повному об'ємі для того, щоб успішно використати перетворення Фур’є (або. як говорять математики, гармонічний аналіз) для рішення практичних задач. Справа в тому. що експериментальні дані, котрі обробляються па комп'ютерах, звичайно представляються у вигляді скінченній (бути може, дуже довгому) послідовності чисел. У цьому випадку застосовується дискретне перетворення Фур'є, з яким працювати набагато легше.

Періодичні функції з періодом 2π можна розглядати як функції на окружності одиничного радіуса. Нехай . Дискретним аналогом цієї окружності служить набір точок (j=1….m), а періодичної функції — періодична послідовність (y₁, y₂,….), . Назвемо дискретним перетворенням Фур'є послідовності наступну (взагалі кажучи, комплексну) послідовність:

(6)

Будь-яка така послідовність може бути легко відновлена за допомогою формули звертання Фур'є:

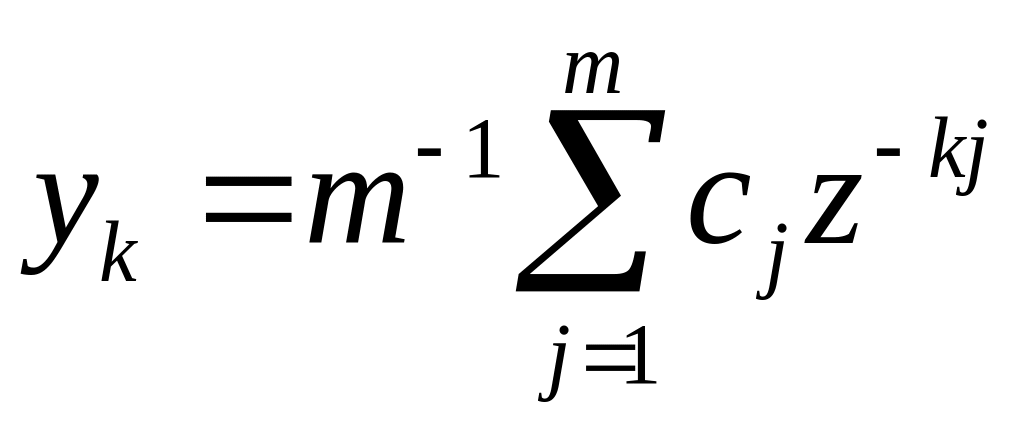(7)

де - коефіцієнти Фур'є, визначенні вище.

Іншими словами, початкова послідовність чисел (яку можна періодично продовжувати в обидві сторони) представлена у вигляді рядка по «елементам гармонікам» з коефіцієнтами с_j .Рівності (6) і (7) є дискретними аналогами співвідношень (4) Фур'є.

Приведемо приклади дискретного перетворення Фур'є при малих значеннях т:

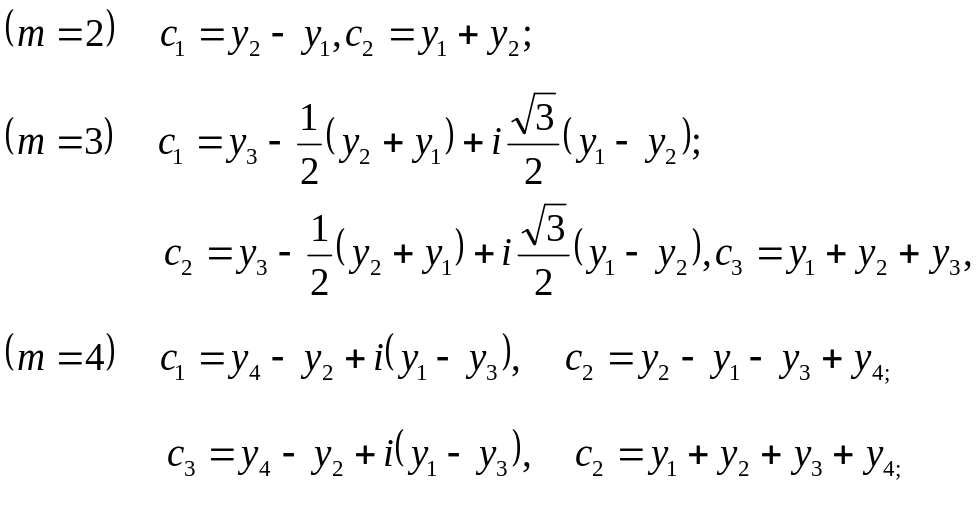
Перевірте що й в загальному випадку с_т = у₁ + у₂+ … + у_т.

Можна зробити, що формула звернення задає представлення послідовності у вигляді тригонометричного полінома, у той час як формула, що визначає перетворення Фур'є, дає коефіцієнти цього полінома.

У багатьох додатках об'єм необхідної числової інформації досить великий навіть для сучасних потужних комп'ютерів. У цьому випадку з’являється проблема стиску даних (тобто скорочення числового масиву таким чином, щоб можна було відтворити вихідні дані з достатньою точністю). Наближення функції з допомогою тригонометричних поліномів часто виявляється корисним при рішенні цієї проблеми.

Припустимо, що значення функції f(x), виміряються в деякому експерименті й за даними y_1,…,y_m нам вдалося чисельно оцінити коефіцієнти Фур'є функції f(x).

Часто виявляється, що функція:

добре наближає функцію f(x), навіть коли число елементарних гармонік n значно менше об'єму даних т. У цьому випадку досить запам'ятати в пам'яті комп'ютера тільки коефіцієнти Фур'є замість вихідного об'єму даних.

Оскільки значення функції відомі експериментатору лише в окремих точках x_i, i =1,…,т, коефіцієнти Фур'є функції f(x) повинні визначатися по цій послідовності. Аналогічна ситуація виникає при обчисленнях на комп'ютерах, якщо аналітичне вираження для функції недоступне або є досить складним.

Тому надалі цікавляться не коефіцієнтами Фур'є безперервних функцій, а коефіцієнтами Фур'є кінцевих послідовностей Ефективна процедура їх обчислення має велике практичне значення. Вона називається швидким перетворенням Фур'є (ШПФ).

Нижче опишемо суть ШПФ. Для прямого обчислення перетворення Фур'є по формулі (6) необхідно здійснити порядку т² операцій множення й порядку т² операцій додавання.

Для багатьох типів комп'ютерів час, потрібний для перемножування чисел, набагато більший від часу, необхідного для додавання чисел. Тому ми будемо намагатися зменшити кількість множення, не звертаючи уваги на кількість додавань.

Багато з чисел які з'являються в (6), в дійсності збігаються. Використаємо цей факт для того, щоб скоротити, число множень. Китайська теорема про залишки може в цьому істотно допомогти.

Припустимо, що число т записується у вигляді т=m₁m_{2 ,}де т₁ i m₂ — взаємно прості числа.

Нехай k₁ i k₂— залишки від ділення індексу k, що з’явився в (6). на т₁ і т₂ відповідно. Аналогічно формулі (9), число k можна представити у вигляді k = k₁М₂m₂ + k₂М₁m₁, де М₁ i М₁ одним образом визначаються із співвідношень М₂m₂ + М₁m₁=1 (mod m). 0 < М₁, М₂ < т.

Тепер представимо перетворення Фур'є, тобто суму в правій частині (6) як подвійну суму по індексах k₁ i k₂, що проходять значення від 0 до т₁ і т₂, відповідно. Нехай також остача від ділення М₂j на т₁, a j₂ — остача від ділення М₁j на т₂.

Помітимо, що j=m₂j₁+ m₁j₂ (mod m). Для доведення досить просумувати рівності M₁j =m₁p, M₂j =m₂p, помножені па m₂ й т₁ відповідно. Тут р и q додатні цілі числа.

Далі, введемо позначення і замітимо, що . Якщо тепер винести загальні множники із внутрішньої суми по індексу j₂ то вийде наступний результат:

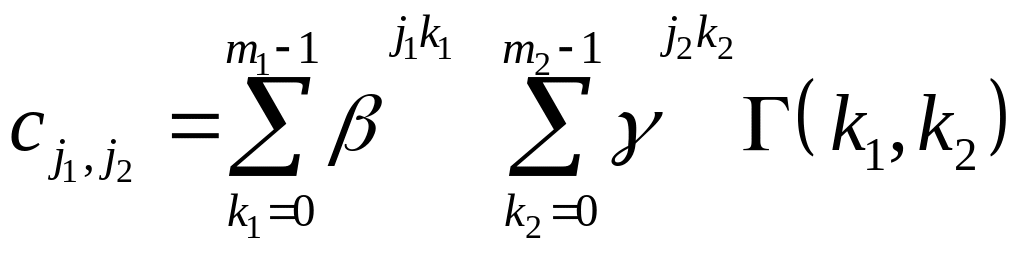(10)

де

Для обчислення однієї внутрішньої суми по формулі (10) потрібно виконати m₂ множень, а для обчислення всіх m₁ внутрішніх сум при k₁=0,…, m₁-1 потрібно виконати т=т₁т₂ множень.

Отже, якщо число т не є простим, ми можемо обчислити перетворення Фур'є за множень. Якщо ми зможемо розкласти m₁ і m₂ на добуток взаємно простих чисел, число множень скоротиться ще більше. Зрозуміло, деякі труднощі виникають через порядок обчислення коефіцієнтів a_j.

Поняття дискретного перетворення Фур'є природно узагальнюється на двовимірний випадок, коли дані утворять не послідовність чисел, а двовимірний масив Перетворення Фур'є цього масиву (матриці) утворить новий масив, елементи якого мають наступний вигляд:

(11)

де

Двовимірне перетворення Фур'є — це не просто математична абстракція, воно корисне в багатьох прикладних задачах, включаючи обробку зображень. Під зображенням ми розуміємо двовимірну таблицю, елементи якої відповідають рівням яскравості фотографії в точці з декартовими координатами де h – розмір елементарної комірки (роздільна здатність) зображення. Ця проста модель зображення досить задовільна при аналізі фотографій поверхні Землі й інших планет, зроблених з космосу.

Перетворення Фур'є дозволяє значно скоротити кількість інформації, яку необхідно використати для відновлення зображення. Звичайно досить запам'ятати лише трохи перших гармонік (коефіцієнтів Фур'є), щоб відтворити зображене прийнятної точності за допомогою оберненого перетворення Фур'є:

Точка над y вказує на те, що тільки приблизно співпадають з у випадку коли

Виявляється, що в багатьох практичних ситуаціях точність такої апроксимації є досить високою, навіть коли К, L значно більше, ніж . В якості прикладу обговоримо використання перетворення Фур'є для стиснення інформації при дослідженні форми морської поверхні. Скористаємося ідеалізованою моделлю припускаючи, що рівень контрастності в будь-якій точці пропорційний висоті морській хвилі. Припустимо також, що довжина хвилі рівна р в деякому напрямку й q перпендикулярному до його направлення, це означає, що:

де А – амплітуда води.

Легко перевірити, що V(j,m)=A , якщо і нулю в інших випадках (для простоти ми припустимо, що - цілі числа). Таким чином, для відновлення цього зображення достатньо знати три числа

У випадку довільного масиву відкидання членів з великими значеннями k i l в сумі (11) приводить до більш згладженому зображенні, ніж початкове. Це скоріше позитивна властивість, оскільки дрібномасштабні флуктуації зазвичай викликані шумом і їх знищення при обробці приводить до поліпшення якості зображення.

Зміст роботи

Для виконання даної лабораторної роботи на ПК, повинен бути встановлений математичний пакет – Matlab 6 або пізнішої версії та додаток до математичного пакету для обробки сигналів – Signal Processing Toolbox. А також необхідно знати поняття одномірного та двомірного дискретного прямого та зворотнього перетворення Фур’є та вміти їх застосувати.

В ході виконання лабораторної роботи потрібно згенерувати сигнал певної частоти, за допомогою якого передаються дані, даний сигнал повинен містити регулярні складові із певними частотами і випадкову адитивну компоненту з нульовим середнім. За допомогою перетворення Фур’є виділити частоти регулярних складових сигналу, зашумленого перешкодами.

Нижче наведений опис та синтаксис функцій дискретних перетворень Фур’є в Matlab, з прикладом виконання роботи.

Одномірне дискретне пряме й зворотне перетворення Фур'є:

Синтаксис:

Y=fft(X) X=ifft(Y)

Y=fft(X,n) X=ifft(Y,n)

Опис:

Дискретні пряме й зворотне перетворення Фур'є для одномірного масиву x довжини N визначаються в такий спосіб:

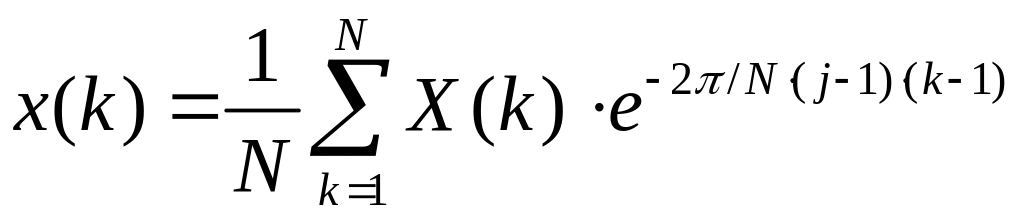
Функція Y=fft(X) обчислює для масиву даних X дискретне перетворення Фур'є, використовуючи FFT-алгоритм швидкого Фур'є-перетворення. Якщо масив X двовимірний, обчислюється дискретне перетворення кожного стовпця.

Функція Y=fft(X,n) обчислює n-крапкове дискретне перетворення Фур'є. Якщо length(X) < n, то відсутні рядки масиву X заповнюються нулями; якщо length(X) > n, те зайві рядки віддаляються.

Функція X=ifft(Y) обчислює зворотне перетворення Фур'є для масиву Y.

Функція X=ifft(Y,n) обчислює n-крапкове зворотне перетворення Фур'є для масиву Y.

Приклад:

Основне призначення перетворення Фур'є – виділити частоти регулярних складових сигналу, зашумленого перешкодами. Розглянемо дані, що надходять із частотою 1000 Гц. Сформуємо сигнал, що містить регулярні складові із частотами 50 Гц й 120 Гц і випадкову адитивну компоненту з нульовим середнім.

t=0:0.001:0.6;

x=sin(2*pi*50*t)+sin(2*pi*120*t);

y=x+2*randn(size(t));

plot(y(1:50),’red’), grid

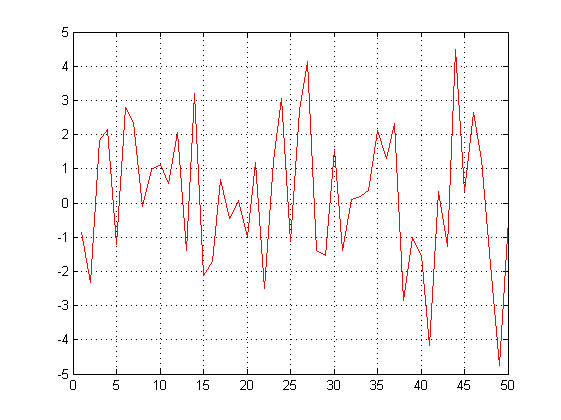
Рис. 2

На рис. 2 показаний цей сигнал. Дивлячись на нього, важко сказати, які частоти його регулярних складових. Реалізуючи одномірне перетворення Фур'є цього сигналу на основі 512 крапок і побудувавши графік спектральної щільності (рис. 3), можна виділити дві частоти, на яких амплітуда спектра максимальна. Це частоти 120 й 50 Гц.

Y=fft(y, 512);

Pyy=Y.*conj(Y)/512;

f=1000*(0:255)/512;

figure(2), plot(f, Pyy(1:256),’red’), grid

Алгоритм:

Якщо довжина послідовності вхідних даних є ступенем числа 2, то застосовується алгоритм швидкого перетворення Фур'є з підставою 2, що має максимальну продуктивність. Цей алгоритм оптимізований для роботи з дійсними даними; якщо дані комплексні, то реалізується комплексне перетворення Фур'є. Ефективність першого на 40 % вище другого.

Якщо довжина вхідної послідовності не є ступенем числа 2, то застосовується перетворення зі змішаними підставами, які визначаються як прості множники довжини вхідної послідовності, що при необхідності піддається усіканню.

Рис. 3

Час розрахунку істотно залежить від значення довжини послідовності. Якщо значення довжини точно розкладається на прості множники, то обчислення для такої послідовності виконуються досить швидко; якщо ж не всі множники виявляються простими, і навіть їх буде менше, той час обчислення істотно зростає.

Якщо порівнювати ефективність обчислень, то перетворення Фур'є з підставою 2 дійсні послідовності з 4096 крапок займає 2.1 з, а комплексної - 3.7 с. Звичайне перетворення Фур'є для послідовності з 4096 крапок займає 7 з, а для послідовності з 4098 крапок - 58 с.

Двовимірне дискретне пряме й зворотне перетворення Фур'є

Синтаксис:

Y=fft2(X) X=ifft2(Y)

Y=fft2(X,m,n) X=ifft2(Y,m,n)

Опис:

Функція Y=fft2(X) обчислює для масиву даних X двовимірне дискретне перетворення Фур'є. Якщо масив X двовимірний, обчислюється дискретне перетворення для кожного стовпця.

Функція Y=fft(X,n) обчислює n-крапкове дискретне перетворення Фур'є. Якщо length(X) < n, то відсутні рядки масиву X заповнюються нулями; якщо length(X) > n, те зайві рядки віддаляються.

Функція X=ifft(Y) обчислює зворотне перетворення Фур'є для масиву Y.

Функція X=ifft(Y,n) обчислює n-крапкове зворотне перетворення Фур'є для масиву Y.

Приклади:

Розглянемо той же приклад, що й для функції fft, але сформуємо 2 вхідні послідовності (рис. 4):

t=0:0.001:0.6;

x=sin(2*pi*50*t) + sin(2*pi*120*t);

y1=x+2*randn(size(t));

y2=x+2*randn(size(t));

y=[y1;y2];

plot(y(1,1:50)),hold on, plot(y(2,1:50)), grid, hold off

Рис. 4

Застосуємо двовимірне перетворення Фур'є для сигналу y на основі 512 крапок і побудуємо графік спектральної щільності (рис. 5). Тепер можна виділити 2 частоти, на яких амплітуда спектра максимальна. Це частоти – 100/2Гц й 240/2Гц.

Y fft2(y, 2, 512);

Pyy=Y.*conj(Y)/512;

f=1000*(0:255)/512;

figure(2), plot(f,Pyy(1:256)), grid

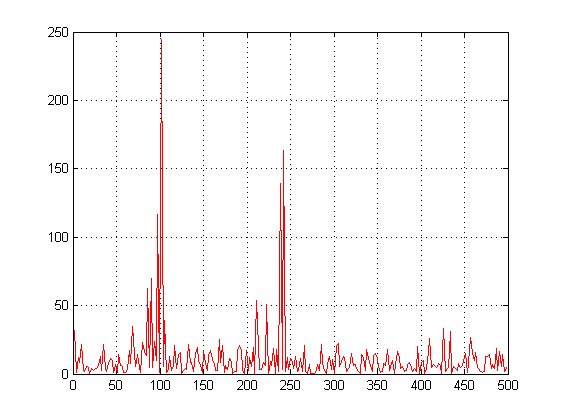
Рис. 5

Алгоритм:

Двовимірне дискретне перетворення пов'язане з одномірним дискретним перетворенням Фур'є в такий спосіб:

fft2(X)=fft(fft(X).’).’