11. Методы описания и анализа систем управления

Для анализа системы автоматического управления и регулирования необходимо располагать ее математическим описанием. Система может описываться Дифференциальными или интегро-дифференциальными уравнениями, уравнениями в частных производных и т. д. Они определяют поведение САУ в переходном процессе.

Уравнения называют уравнениями динамики, если они описывают изменение входящих в них переменных во времени. Из уравнений динамики можно получить уравнения статики, если положить входящие в них производные и воздействия равными нулю или постоянными величинами. Уравнения статики описывают поведение системы в установившемся режиме.

В соответствии с классификацией систем управления (рис. 24) кратко рассмотрим методы решения задач описания, анализа и синтеза линейных и нелинейных непрерывных систем управления. Сюда относят методики решения задач 1 анализа выходных процессов, устойчивости, управляемости и наблюдаемости линейных САУ. При этом используются все известные формы математического описания систем: дифференциальными уравнениями, переходными функциями, интегральными и спектральными преобразованиями.

В основе лежит представление системы в виде соединений образующих ee звеньев: последовательного, параллельного, с обратной связью, и замена сложной структуры эквивалентным звеном - оператором системы, преобразующим входной сигнал в выходной.

При исследовании нелинейных систем рассматривают задачи анализа выходных процессов при детерминированных и случайных воздействиях, анализа, абсолютной устойчивости нелинейной САУ; применяются методы гармонической и статистической линеаризации.

К современным проблемам управления можно отнести разработку методики решения задач оптимального управления детерминированными и стохастическими системами с применением принципа максимума и уравнения Беллмана, а также разработку алгоритмов синтеза систем совместного оценивания (наблюдателей состояния) и управления.

11.1. Линейные системы управления

11.1.1. Описание и анализ линейных систем с помощью дифференциальных уравнений

11.1.1.1. Одномерные системы при детерминированных воздействиях

Непрерывные процессы, протекающие в таких системах управления, описываются обыкновенными дифференциальными уравнениями (ОДУ) с соответствующими начальными условиями. Тогда, если известен вид входного сигнала, выходной сигнал определяется в результате решения задачи Коши для ОДУ.

Линейная нестационарная система описывается уравнением

(11.1)

с начальными условиями

(11.2)

где g(t) - входной сигнал, y(t) - выходной сигнал, t - текущее время, а_i (t), b_j(t)- коэффициенты уравнения.

Если коэффициенты а_i (t), b_j(t) уравнения (11.1) постоянны, система называется линейной стационарной.

Уравнение (11.1) может быть записано в операторной форме:

(11.3)

где оператор дифференцирования, D(p,t) и M(p,t) - собственный и входной операторы уравнения (11.1).

Для линейной стационарной системы уравнение в операторной форме имеет вид

(11.4)

Из операторной формы записи уравнения следует способ изображения стационарной системы (ее звеньев) на структурных схемах (рис. 27).

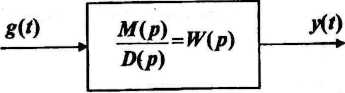
Рис. 27. Структурная схема стационарной системы

W(p) называют передаточной функцией. Строгое определение передаточной функции вводится через преобразование Лапласа при нулевых начальных условиях.

Звено любого физического вида и конструкции, описываемое дифференциальным уравнением или передаточной функцией первого и второго порядка называют типовым динамическим звеном. Описание типовых динамических звеньев рассматривается в курсе теории автоматического регулирования и управления.

По дифференциальным уравнениям типовых звеньев и связям между ними составляются структурные схемы систем. Они служат одним из языков описания систем управления.

Рассмотрим в качестве примера дифференциальное уравнение инерционного звена первого порядка:

Преобразуем это уравнение. Старшую производную (в данном случае производная одна) оставляем слева, остальные слагаемые переносим в правую часть:

Далее построим структурную схему (рис. 28)

y₀

K / T

1/ P

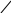
g(t) + y(t)

–

y

1/ T

(t)

Рис. 28. Инерционное звено первого порядка

Методика представления САУ в виде структурных схем используется, в частности, при решении задач с помощью аналоговой и цифровой вычислительной техники.

По структурной схеме всегда можно составить дифференциальные уравнения системы.

Анализ выходных процессов может быть проведен по результатам решения дифференциальных уравнений аналитическими методами, численными методами на ЭВМ или интегрированием дифференциальных уравнений по структурным схемам на аналоговой вычислительной технике.

Для линейных систем справедлив принцип суперпозиции: эффект, вызываемый суммой нескольких воздействий, равен сумме эффектов каждого из воздействий в отдельности. Поэтому выходной сигнал линейной САУ при аналитическом решении представляется в виде суммы свободного и вынужденного движений:

(11.5)

11.1.1.2. Линейные многомерные системы управления

Одна из типичных задач при управлении технологическими процессами – анализ многомерных систем управления.

Если рассматриваемая модель процесса линейная, то её можно представить в виде следующей системы уравнений в пространстве состояний (во временной области):

, (11.6)

с начальными условиями (t₀) = , а уравнение выхода - в виде

(11.7)

Здесь - n-мерный вектор состояний, - вектор начальных состояний,

- т-мерный вектор управлений, - k-мерный вектор возмущений, - l - мерный вектор наблюдений (выходных координат, или измерений), A, В, С, Г - матрицы соответствующих размерностей, которые в общем случае могут зависеть от времени.

Рассмотрим пример. Необходимо записать уравнения состояния и выхода (измерений) многомерной системы в матричной форме. Имеем:

Определяем размерности сигналов: n = 2, m = 1, l= 1 и записываем соответствующие уравнения:

Выпишем аналитическое решение уравнений (11.6) и (11.7). В случае стационарной (автономной) системы (матрицы А, В, С, Г не зависят от времени) можно воспользоваться преобразованием Лапласа

(11.9)

где Е - единичная матрица.

Разрешая полученные уравнения в преобразованиях относительно X(s), найдем

(11.10)

Возвращаясь к оригиналам, с помощью теоремы о свертке получим для (t) выражение

(11.11)

где e^At - экспоненциал матрицы A(t), определяемый как решение однородного матричного линейного дифференциального уравнения

(11.12)

где А - вектор размерности п.

Если все собственные числа матрицы А (корни характеристического уравнения) различны, существует каноническое преобразование, приводящее матрицу к диагональному виду:

(11.13)

где

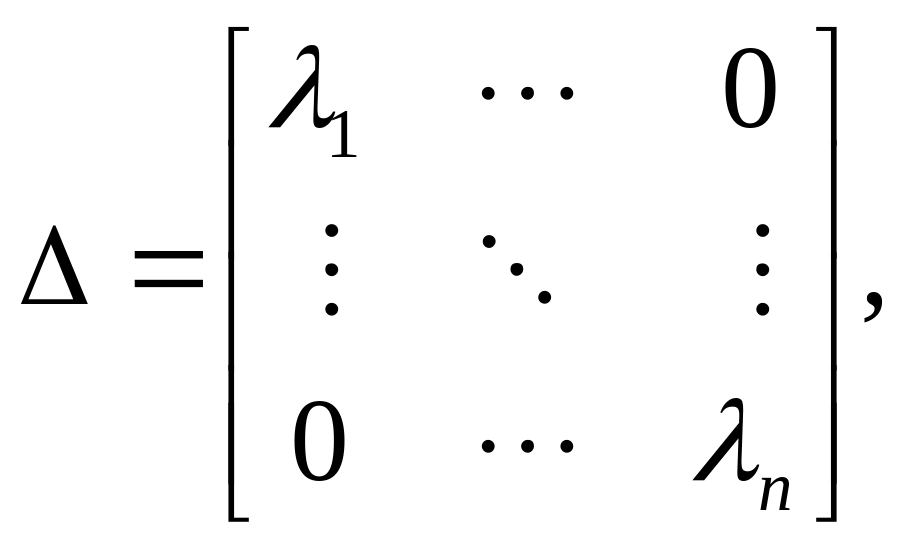(11.14)

есть диагональная матрица собственных чисел А; М - матрица собственных векторов.

Подставив выражение (11.13) в (11.12), получим

(11.15)

Решением последнего уравнения является выражение

(11.16)

откуда

(11.17)

где

(11.18)

есть диагональная матрица.

В случае нестационарной (неавтономной) системы (матрицы А,В,С,Г зависят от времени) решение уравнений (11.6) и (11.7) имеет вид

(11.19)

где матрица Ф(t,t₀) размерностью (nхn) называется фундаментальной матрицей (переходной матрицей Коши) системы (11.6) и (11.7) и определяется как решение матричного дифференциального уравнения

(11.20)

с начальными условиями

(11.21)

Первое слагаемое в (11.19) описывает свободное движение, второе - вынужденное.

При анализе динамики линейных многомерных систем с постоянными параметрами можно использовать представление во временной области, т. е. в пространстве состояний (11.6) - (11.7), или же представление в области комплексной переменной s = α + jω, т. е. в частотной области:

, (11.22)

где G(s) и G_D(s) - матричные передаточные функции, связывающие управление U(s) и возмущение d(s) с выходом Y(s).

Переход от представления уравнений (11.6) и (11.7) к представлению (11.22) единствен и осуществляется путем применения к уравнениям преобразования Лапласа:

(11.23)

откуда

(11.24)

Для выполнения расчетов на ЭВМ по выражениям (11.23) - (11.24) разработаны специальные программы.

Обратный переход к временному представлению сложнее. Можно построить целое семейство уравнений (11.6) - (11.7), то есть передаточная функция может соответствовать нескольким различным моделям динамики в пространстве состояний.

11.1.2. Описание и анализ линейных систем с помощью переходных функций

В случае, когда система управления описывается дифференциальными уравнениями или известна ее импульсная переходная функция w(t,r), вынужденное движение системы, то есть закон изменения выходного сигнала при нулевых начальных условиях, для нестационарной одномерной системы определяется по формуле

, (11.25)

Д ля многомерных нестационарных систем соотношения аналогичны. Вектор состояния x(t) и вектор выхода y(t) описываются следующим образом:

, (11.26)

,

где τ - момент приложения входного сигнала (возможен случай t₀ = - ∞). Импульсные переходные функции находятся по формулам:

(11.27)

где Ф(t,τ) - переходная матрица.

При случайных воздействиях входной сигнал обычно задают статистическими характеристиками т_g (t), К_g (t₁,t₂) и находят статистические характеристики сигнала состояния т_x (t), К_x (t₁,t₂):

(11.28)

11.1.3. Описание и анализ линейных систем с помощью интегральных преобразований

Для анализа систем автоматического управления применяются интегральное преобразование Лапласа и интегральное преобразование Фурье.

11.13.1. Преобразование Лапласа

Преобразование Лапласа сигнала g(t) имеет вид

(11.29)

где G(s) - изображение сигнала по Лапласу, - комплексная переменная.

Преобразование Лапласа позволяет перейти к описанию звеньев и систем при помощи передаточных функций и составлению структурных схем САУ.

Передаточной функцией W(s) стационарной линейной системы называется преобразование Лапласа импульсной переходной функции W(η):

(11.30)

где η =t-τ.

В курсе теории автоматического регулирования и управления рассматривается нахождение передаточных функций по структурной схеме, а также методы преобразования структурных схем.

Анализ выходных процессов линейных систем ведется по следующей схеме:

1. Находится изображение входного сигнала G(s) = L{g(t)};

2. Определяется передаточная функция Ф(s) системы;

3. Определяется изображение по Лапласу выходного сигнала

;

4. Находится выходной сигнал с помощью обратного преобразования Лапласа:

, (11.31)

Интегрирование ведется по прямой Re s = c в области аналитичности функции Y(s) с применением теории вычетов или таблицы преобразования Лапласа.

Рассмотрим пример. Необходимо найти реакцию системы, описываемой дифференциальным уравнением

на входной сигнал g(t) = 1(t) при нулевых начальных условиях.

1. Изображение входного сигнала:

.

2. Передаточная функция:

3. Изображение по Лапласу выходного сигнала:

4. Выходной сигнал:

.

Установившееся значение реакции динамической системы можно получить по изображению выходного сигнала, воспользовавшись свойством преобразования Лапласа (предполагается, что Re s>0):

t→∞ s→0 (11.32)

Для стационарной линейной многомерной САУ передаточной функцией состоянию

W ^x(s) называется преобразование Лапласа импульсной переходной функции по состоянию:

(11.33)

Аналогично определяется передаточная функция по выходу:

(11.34)

Передаточные функции W ^x(s) и W ^y(s) представляются матрицами размера (n x т) и (l х m) соответственно, а элементы матриц являются функциями комплексного переменного s. Они могут быть найдены по формулам:

(11.35)

Сравнивая (11.35) с (11.27), получаем еще один способ нахождения переходной матрицы:

(11.36)

где L^-1 - обратное преобразование Лапласа.

В этом случае анализ выходных процессов производится по следующей cxeме.

Пусть известен входной сигнал g(t), а линейная стационарная многомерная система описывается уравнениями

,

(11.37)

где А,В,С -матрицы размера (nхn), (nхm) и (lхn) соответственно. Начальные условия:

Требуется найти законы изменения вектора состояния x(t) и вектора выхода y(t), т. е. определить связи вход-состояние и вход-выход.

П рименяя преобразование Лапласа к левой и правой частям уравнений состояния и выхода, имеем

,

(11.38)

Отсюда

(11.39)

Учитывая (11.35), получаем

,

(11.40)

Первые слагаемые в (11.40) представляют собой изображения по Лапласу свободного движения, а вторые - вынужденного.

11.13.2. Преобразование Фурье

Для детерминированного сигнала преобразование Фурье определяется по формуле

(11.41)

Характеристики стационарных случайных процессов:

- спектральная плотность

(11.42)

где К_g (η) - корреляционная функция стационарного случайного процесса;

- дисперсия (определяется обратным преобразованием Фурье):

(11.43)

Частотной характеристикой (АФЧХ) W(jω) стационарной линейной системы называется преобразование Фурье импульсной переходной функции:

(11.44)

Существует связь между частотной характеристикой и передаточной функцией:

(11.45)

s= jω

Частотная характеристика является комплексно-значной функцией вещественного аргумента ω - частоты, изменяющейся в промежутке от 0 до ∞, и может быть представлена в показательной, тригонометрической и алгебраической формах:

,

(11.46)

Здесь А(ω) - амплитудная частотная характеристика (АЧХ) системы,

(11.47)

φ(ω) - фазовая частотная характеристика (ФЧХ),

(11.48)

Частотная характеристика W(jω) изображается годографом в координатах U и V или в полярных координатах А и φ, который называется амлитудно - фазовой частотной характеристикой (рис. 29).

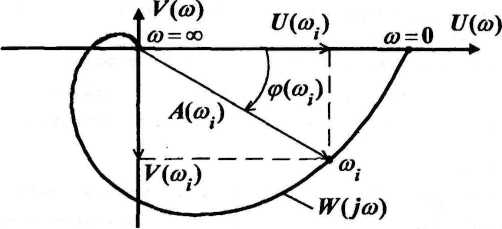
Рис. 29. Амлитудно-фазовая частотная характеристика

Преобразование Фурье используется при анализе выходных процессов в САУ при случайных воздействиях и при анализе устойчивости САУ. В курсе теории автоматического регулирования и управления рассматриваются частотные методы анализа устойчивости замкнутых САУ: критерий Михайлова и критерий Найквиста, которые основаны на построении годографов D(jω) - характеристического полинома САУ, и W(jω) - АФЧХ разомкнутой системы.

11.1.4. Описание и анализ линейных систем с помощью спектральных преобразований

Представление процессов рядами является весьма универсальной формой их описания. Эту форму можно рассматривать как промежуточную между описанием процессов во временной области и интегральными преобразованиями.

К первому способу данная форма тяготеет в тех случаях, когда оперирует собственно рядом как функцией времени; ко второму - когда коэффициенты ряда отделяются от собственно ряда и во всех вычислительных операциях используется лишь совокупность этих коэффициентов.

Последний подход привел к введению спектральной формы описания процессов. В этой форме временные процессы рассматриваются на конечных, в общем случае нестационарных интервалах времени.

В процессе решения задач производятся алгебраические операции с матрицами. Практическое использование спектрального метода обеспечивается различными библиотеками стандартных программ.

11.1.5. Устойчивость, управляемость и наблюдаемость линейных стационарных систем

Для выяснения качественных особенностей поведения систем управления, т.е. для решения задачи анализа выходных процессов, вводятся понятия устойчивости, управляемости, стабилизируемости, нормализуемости и наблюдаемости.

11.1.5.1. Устойчивость

В соответствии с представлением выходного сигнала в виде (11.5) система управления называется устойчивой по начальным данным, если при ненулевых ограниченных начальных условиях свободное движение У_своб(t) ограничено при всех

и .

Система управления называется устойчивой по входу, если при любом ограниченном воздействии g(t) реакция системы у_вын.(t) является ограниченной в любой момент времени

.

Термин "устойчивая система управления" употребляется, если система устойчива и по входу, и по начальным данным.

Для определения устойчивости применяют критерии устойчивости:

- действительные части корней λi характеристического уравнения САУ

det(A -λE) = 0 должны быть отрицательными;

- критерий Гурвица;

- частотные критерии Найквиста и Михайлова.

11.1.5.2. Управляемость

П ри анализе систем управления существенным является понятие управляемости. Система называется полностью управляемой, если из любого начального состояния x(t₀) она может быть переведена в любое наперед заданное состояние x(t) с помощью некоторого управления u(t) за конечное время t-t₀ ≥0.

Управляемость является внутренним свойством систем. Возможен случай частично управляемой системы, т.е. системы, имеющей подмножества начальных состояний, из которых достижение произвольного желаемого состояния за конечное время невозможно.

К ритерий управляемости формулируется следующим образом. В случае постоянных матриц А и В система (11.40) будет полностью управляема по состояниям тогда и только тогда, когда ранг (n x nт) матрицы управляемости L_c, которая рассчитывается по формуле

(11.49)

равен размерности вектора состояния:

rang L_c = n . (11.50)

11.1.5.3. Стабилизируемость

Свойство стабилизируемости является более слабым, чем свойство управляемости. Оно заключается в том, что с помощью воздействия регулятора в цепи обратной связи все неустойчивые моды или собственные векторы управляемой системы могут быть сделаны устойчивыми. Другими словами, все положительные вещественные части собственных чисел могут быть сделаны отрицательными. Понятно, что всякая управляемая система стабилизируема.

Например, если рассматривается случай регулирования по выходам, т.е.

, (11.51)

то система (11.40) приводится к виду

(11.52)

где К - матрица обратной связи размерностью (тхп).

Стабилизируемость обеспечивается таким выбором матрицы К, который гарантирует отрицательность всех действительных частей собственных чисел матрицы (А — ВКС)

11.1.5.4. Нормализуемость

Н ормализуемость является наиболее сильной формой управляемости. Система является нормализуемой, если каждая координата вектора управления u(t) в отдельности обеспечивает управляемость. Нужно отметить, что для скалярных управлений u(t) управляемость и нормализуемость совпадают.

11.1.5.5. Наблюдаемость

С истема управления называется вполне наблюдаемой, если по реакции у(t) на выходе системы на интервале времени t-t₀≥0 при заданном управляющем воздействии u(t) можно определить начальное состояние x(t₀).

Р ассмотрим критерий наблюдаемости. Для того, чтобы система была вполне наблюдаемой, необходимо и достаточно, чтобы ранг матрицы наблюдаемости

(11.53)

равнялся размерности вектора состояния:

rang Q=n. (11.54)

Приведем пример использования данного критерия. Необходимо исследовать управляемость и наблюдаемость системы

1. В уравнениях состояния и выхода выделим матрицы А, В, С:

2. Составим матрицы управляемости и наблюдаемости:

3. Определим ранги матриц:

rang L_c=2=n,

rang Q=2=n.

Согласно критериям управляемости (11.50) и наблюдаемости (11.54) данная система является вполне управляемой и наблюдаемой.

11.1.6. Структурная схема многомерной замкнутой линейной системы автоматического регулирования

Анализ многомерных систем управления с обратными связями проводится на основе аппарата перехода от временного представления линейных многомерных систем с постоянными коэффициентами к их частотному представлению и обратно.

Структурная схема многомерной замкнутой линейной системы регулирования изображена на рис. 30.

d₁

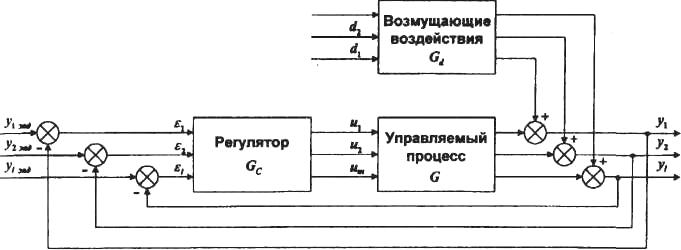
Рис. 30. Структурная схема многомерной САР

Здесь G_c - матрица (на практике обычно диагональная) многомерного регулятора:

(11.55)

Элементы g_iic , соответствующие одноконтурным (одномерным) регуляторам, как правило, задают ПИД-закон в частотной

i=1,2,…,l (11.56)

или во временной области:

(11.57)

где ε_i(t)-ошибка регулирования.

Выход системы определяется выражением

(11.58)

а передаточные функции замкнутой системы по управлению и возмущению -соответственно по формулам:

(11.59)

Тогда (11.60)

11.2. Нелинейные системы управления

Для описания поведения нелинейных систем используются общие теоремы динамики или уравнения Лагранжа второго рода. После преобразования этих дифференциальных уравнений второго порядка к системе уравнений первого по-рядка, разрешенных относительно производных обобщенных координат и обоб-щенных скоростей, получим уравнение движения системы управления:

(11.61)

где y_i(t) - выходные сигналы, g_i(t) - входные сигналы САУ, t_o – момент

начала движения, у_io - начальные значения выходных сигналов.

Поскольку система уравнений (11.61) описывает эволюцию состояния систе-мы управления, векторную запись этих уравнений,

(11.62)

Применение рассмотренных выше методов исследования линейных САУ для нелинейных систем общего вида невозможно. Однако среди нелинейных систем выделяют класс систем управления с одним нелинейным элементом, для которых разработанный аппарат применим с незначительными изменениями.

Широкое применение на практике получили нелинейные элементы с негладкой статической характеристикой (релейные, с зоной нечувствительности, с петлей гистерезиса и др.).

Наличие нелинейного звена придает системе управления свойства, присущие только нелинейным системам (например, автоколебания, "скользящее движение").

С другой стороны, поскольку нелинейный элемент один, то для упрощения анализа той или иной особенности поведения системы его можно заменить тем или иным эквивалентным линейным звеном. При этом используются различные методы линеаризации (в частности, методы гармонической и статистической линеаризации, метод В. М. Попова). Они рассматриваются в курсе теории автоматического регулирования и управления.

Для исследования свободного движения автономных систем, описываемых дифференциальными уравнениями второго порядка.

(11.63)

где f(y,y) - кусочно-непрерывная функция, применяется метод фазовой плоскости.

Уравнение (11.63) переписывается в виде системы двух уравнений первого порядка:

(11.64)

Далее исключается время путем деления второго уравнения на первое. В результате получаем уравнение фазовых траекторий системы:

(11.65)

Решение уравнения v = v(y) называется фазовой траекторией, производ- ная dv/dy фазовой скоростью.

Графики фазовых траекторий строятся на фазовой плоскости в координатах

у и v =dy/dt. Изменению положения системы (11.63) с течением времени соответствует движение изображающей точки (y(t), v(t)) по фазовой траектории. Тем самым анализ свободного движения сводится к построению фазовых траекторий системы (11.63), которые показывают ее поведение на фазовой плоскости.

Если в системе присутствуют нелинейные элементы, имеющие релейный характер (или элементы с зоной нечувствительности, с зоной неоднозначности), то фазовую плоскость разбивают на области, и для каждой области записывают со-ответствующее уравнение фазовых траекторий. Затем строят фазовую траекторию в области, содержащей начальную точку (y₀, v_o). Если фазовая траектория, исходящая из точки (y₀, v_o) , достигает границы, отделяющей начальную область от соседней, то следует найти координаты (у, v) точки ее пересечения с границей. Эти координаты используются в качестве начальных условий для решения уравнения фазовых траекторий, соответствующего соседней области. Отметим, что на границе областей фазовая траектория непрерывна, а фазовая скорость dv/dy— может терпеть разрыв. Построение фазовых траекторий, и в особенности фазовых портретов систем автоматического регулирования, рассматривается в курсе теории автоматического регулирования и управления.

11.3. Проблема многосвязности

При синтезе многомерных систем регулирования значительные затруднения связаны с наличием статических и динамических перекрестных связей между различными входами и выходами системы.

Если такие связи отсутствуют, а число управляющих воздействий равно числу наблюдаемых координат, то матричная передаточная функция разомкнутой; системы будет диагональной:

(11.66)

Если диагональна также и матрица управления , то такой же будет матричная передаточная функция замкнутой системы, связывающая задание с выходом . При этом каждый отдельный контур регулирования может настраиваться независимо от остальных с использованием обычных методов классической теории регулирования.

К сожалению, для большинства многомерных задач регулирования характерна многосвязность по входам и выходам. Эффективность управления может быть значительно увеличена за счет использования более сложной системы, минимизирующей влияние взаимосвязей.

Неоднократно делались попытки определить степень связности многомерной системы. Наиболее широко используется для этого матрица Бристоля, характеризующая степень связности в статике.

Матрица Бристоля - это матрица вида

(11.67)

элементы которой определяются в статике следующим образом:

(11.68)

Анализ матрицы Λ позволяет указать несколько общих характеристик матриц Бристоля:

-сумма элементов любой строки или любого столбца равна единице:

- если передаточная матрица диагонапьна или треугольна, то соответст вующая матрица Бристоля единична.

Из определения меры связности понятно, что наилучшей возможной ситуацией является близость к нулю недиагональных элементов и близость к единице диагональных элементов матрицы Бристоля:

(11.69)

В этом случае взаимосвязи несущественны, и поведение замкнутой системы аналогично поведению разомкнутой. Когда недиагональные элементы возрастают по модулю, а диагональные убывают, степень связности увеличивается.

Матрица Бристоля может служить основным средством для формирования; пар вход-выход.

Для динамических связей общепринятой меры связности, подобной матрице Бристоля, не существует.

Для улучшения качества многомерных систем регулирования применяют различные методы компенсации (или развязывания) перекрестных связей. Наиболее известным является метод синтеза стационарной автономной системы, заключающийся в определении передаточной матрицы компенсатора.

Однако автономное регулирование не всегда оказывается эффективным.

Е сли передаточная матрица объекта G (s) содержит элементы чистого запаздывания, то динамический компенсатор, как правило, должен включать элементы опережения, использующие будущие значения выходов. В чистом виде элементы опережения не могут быть реализованы, однако часто удается получить неплохие результаты, используя вместо них различные прогнозаторы. Слабым местом автономных систем является:

• п риближенность модели G (s) при синтезе системы управления;

• наличие неустойчивых звеньев, компенсация которых затруднительна;

• возможное ухудшение динамических характеристик замкнутой системы при компенсации перекрестных связей.

Влияние статических перекрестных связей, вызванных изменениями задающих воздействий, можно исключить, применив компенсацию задающих воздействий. Это реализуется в системах управления, инвариантных или комбинированных по задающему воздействию.

Недостатком систем с автономностью по задающим воздействиям является то, что компенсатор не стоит в цепи обратной связи, и, следовательно, не улучшает качества системы по отношению к возмущениям.

Еще один подход к синтезу многомерных САУ дает теория модального управления. Она главным образом основывается на линейности рассматриваемых моделей. С помощью этой теории можно устанавливать желаемые значения собственных чисел замкнутой системы (корней характеристического уравнения).

Для синтеза модального управления необходимо точно знать матрицу А и иметь возможность измерять все состояния.

Кроме вышеназванных, имеется еще целый ряд процедур (как правило, человеко-машинных) синтеза многомерных систем управления, позволяющих с помощью ЭВМ итеративно выбирать параметры обратных связей. Итерации продолжаются до тех пор, пока не будет обеспечено желаемое качество замкнутой системы.