6. Содержание отчета

7.1. Титульный лист отчета.

7.2. Наименование и цель работы.

7.3. Исходные параметры стержней, основные расчетные зависимости по п.11. раздела 5.

7.4. Протокол испытания на устойчивость.

7.5. Диаграмма "нагрузка–прогиб".

6.5. Критическое напряжение (на основе формулы Эйлера) для двух стержней.

7.6. Теоретическое значение прогиба пружины при предельной нагрузке для двух стержней.

7.7. Сравнение опытных значений прогиба с теоретическими для двух стержней при предельной нагрузке.

7.8. Выводы.

7. Контрольные вопросы

1. В чем заключается явление потери устойчивости сжатого

стержня?

2. Какая сила называется критической силой и от чего она зависит?

3. Какое дифференциальное уравнение из теории изгиба

лежит в основе вывода формулы Л. Эйлера?

4. Что называется гибкостью стержня? Приведите формулу.

5. В чём заключается различие в поведении идеальных и реальных стержней (стержней с начальными несовершенствами) при сжатии?

6. Как учитывается различное закрепление концов стержня

при определении критической силы?

7. Каков предел применимости формулы Л. Эйлера?

8. Как определяется предельная гибкость для формулы Л.

Эйлера?

9. Какая нагрузка называется критическая?

10. Как определяется критическая сила при напряжениях,

превышающих предел пропорциональности материала?

11. Какой вид имеет график изменения критической силы в

зависимости от гибкости (или длины) для стальных стержней?

8. Пример

Расчет с помощью таблиц φ(λ) осуществляется в следующем порядке:

1. Задаются значением коэффициента φ =0.5.

2. Устанавливают [σ_у], А=F/[σ_у], подбирают размеры сечения.

3. Находят J_min, i_min и .

4. Определяют новое значение φ₁. Если φ₁ значительно отли­чается от φ, то в качестве второго приближения берут φ₂ = (φ+ φ₁)/2 и повторяют расчет. Обычно требуется 2-3 попытки.

Считают сечение подобранным удовлетворительно, если σ и [σ_у] отличаются не более чем на 5%.

Пример. Стойка квадратного сечения длиной 1=1 м с шарнирно закрепленными концами (см. схемы 1и 3) нагружена осевой силой Р = 40 кн. Подобрать размеры сечения при основном допускаемом напряже­нии на сжатие [σ]=160 н/мм2 (сталь Ст. 3).

Решение. Для квадратного сечения со стороной а радиус инерции

Задаемся значением φ = 0,5; т. е. принимаем допуска­емое напряжение при сжатии с учетом возможности про­дольного изгиба

[σ_у] =0,5 [σ_с] =0,5·160=80 н/мм². Необходимая площадь сечения

Сторона сечения

радиус инерции

i_min=0,29 a = 0,29 • 22,4 = 6,7 мм.

При найденных размерах вычислим гибкость

По табл. для = 150, φ = 0,32. Поэтому допускаемое напряжение

[σ_у] = 0,32-160 = 51,2<80 н/мм².

Следовательно, выбранное сечение мало, и его надо увеличить. Новое значение φ найдем, как среднее арифметиче­ское:

φ = (0,5 + 0,32)/2 =0,41

Тогда

[σ_у]= 0,41 • 160 = 65,6 н/мм². При новом допускаемом напряжении

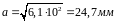
Тогда

По табл. 7

для = 130, φ = 0,40;

для = 140, φ = 0,36;

для =139

Следовательно,

| σ_у|=0,364• 160 =58,2 < 65,6 н/мм².

Размеры сечения вновь недостаточны. Опять возьмем полусумму значений φ:

φ = (0,41 +0,364)/2 = 0,387.

Тогда

[σ_у] = 0,387 • 160 = 62. н/мм²

Поэтому

По табл. находим φ = 0,38. Тогда

[σ_у] = 0,38 [σ_с] = 0,38 • 160 = 60,8 н/мм².

Это допускаемое напряжение близко к рабочему на­пряжению, возникающему в поперечном сечении стерж­ня

Следовательно, необходимо принять а = 25,5 мм.