МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Томский государственный университет

систем управления и радиоэлектроники

(ТУСУР)

ИСПЫТАНИЕ ПРЯМЫХ ГИБКИХ СТЕРЖНЕЙ НА СЖАТИЕ

Методические указания

к выполнению лабораторных работ

по прикладной механике

для студентов всех специальностей

Томск

2013

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Томский государственный университет

систем управления и радиоэлектроники

(ТУСУР)

Кафедра механики и графики (МиГ)

УТВЕРЖДАЮ

Зав. кафедрой МГ

________ Люкшин Б.А.

Механика

ИСПЫТАНИЕ ПРЯМЫХ ГИБКИХ СТЕРЖНЕЙ НА СЖАТИЕ

Методические указания

к выполнению лабораторных работ

по механике и прикладной механике

для студентов всех специальностей

Указания рассмотрены и

одобрены на методическом

семинаре кафедры МиГ,

протокол.

Разработчик

Доцент кафедры

механики и графики

_________ Реутов А.И.

"___"____________ 2013 г.

Томск

2013

СОДЕРЖАНИЕ

1. Цель работы . . . . . . . . . . 4

2. Краткие теоретические сведения . . . . . . 4

3. Оборудование, материалы и инструмент. . . . . . 9

4. Подготовка установки к работе. . . . . . . . 10

5. Порядок выполнения работы. . . . . . . . . 10

6. Содержание отчета. . . . . . . . . . 12

7. Контрольные вопросы. . . . . . . . . . 12

8. Пример . . . . . . . . . . . 12

9.Задача . . . . . . . . . . . . 14

Введение

Для надежной работы изделий и конструкций необходимо, чтобы детали, элементы конструкции обеспечивали необходимую прочность и были устойчивы. При действии внешних нагрузок они должны деформироваться в определенных пределах. Это связано с тем, что при потере устойчивости напряжения быстро нарастают, что может привести к разрушению деталей, элементов конструкции и изделия в целом. Поэтому в целом ряде случаев, в частности, для сжатых стержней, кроме расчета на прочность, необходим и расчет на устойчивость.

1. Цель работы

экспериментальное и теоретическое исследование поведения гибкого стержня при сжатии, построение диаграммы "нагрузка-прогиб", определение критической нагрузки.

сопоставление экспериментально полученной осадки пружины с рас­четной.

2. Краткие теоретические сведения

Под устойчивостью понимается свойство системы сохранять свое состояние при внешних воздействиях. Если система таким свойством не обладает, она называется неустойчивой. В реальных условиях всегда существуют какие-то причины, по которым может произойти отклонение от исходного равновесного состояния. В этом случае говорят, что произошла потеря устойчивости.

Наиболее простым случаем является потеря устойчивости централь­но сжатого стержня (рис. 1).

Рис.1.

Если сжимать стержень продольными силами до тех пор пока сжимающие силы не превзойдут некоторой величины, стержень будет испытывать обычное сжатие и ось его будет оставаться прямолинейной.

Однако если сжимающие силы станут больше предельной величины, то стержень внезапно выпучится и ось его изогнется. Произойдет потеря ус­тойчивости. Величина этой силы зависит от длины стержня и жесткости его поперечного сечения.

Предельное значение силы, при которой прямолиней­ная форма равновесия из устойчивой переходит в не­устойчивую, называется критической силой. Если нагрузка меньше критической величины, то возможна только одна прямолинейная форма устойчивого равновесия.

Стержням, работающим на сжатие, должны, конечно, придаваться такие размеры поперечных сечений, при которых критическая сила была бы значи­тельно больше силы, фактически действующей на стер­жень.

Если обозначить критическую силу Р_кр, а допускае­мую силу Р_д, то отношение P_кр/P_д = n > l называется запасом устойчивости.

n_{у =} P_кр/P_д ≥ [n_у]

где [n_у] — требуемый (допускаемый) коэффициент запаса устойчивости; для стальных стержней металлоконструкций [n_у] = 1,7—2,0; для деталей машин (домкраты, ходовые винты) [n_у] = 3,0—5,0.

Запас устойчивости, также как и запас прочности, неоднородных материалов берется выше, чем для однородных.

Исследование поведения гибкого стержня при сжатии предполагает анализ его устойчивости и определение условий потери устойчивости.

Сила, при которой стержень теряет устойчивость, носит название критической силы.

Задача устойчивости решается на основе модели идеального стержня. Считается, что ось стержня строго прямолинейна; внешние силы, включая реакции связей, приложены строго центрально.

Величина критической силы зави­сит от закрепления концов стержня.

Рассмотрим стержень с шарнирно-опертыми концами (рис. 2).

Под действием сжимающей силы, равной критической силе или несколько больше ее, стер­жень изогнется. Изгибающий момент в любом сечении стержня будет равен:

М = -Fу, ( )

т. е. сама нагрузка (изгибающий момент) зависит от деформации (изгиба) стержня.

Для вывода этой формулы примем, что изогнутая упругая линия стержня пред­ставляет собой синусоиду. Обозначим через f величину стрелы про­гиба посредине стержня, тогда уравнение упругой линии будет:

( )

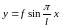Рис. 2.

На концах стержня при х = 0 и х = l , у = 0, т. е. прогиба не будет. Посредине стержня, т. е. при х — l/2, прогиб, как не­трудно видеть из уравнения (252), будет равен f .

Подставив значение у из уравнения (252) в выражение изгибающего момента (а), получим:

(б)

Подставив это выражение момента в общее уравнение упругой линии (196):

получим:

Так как при x = l/2, y = f , то

или

(1)

Здесь Е – модуль продольной упругости материала стерж­ня,

I_min – минимальный момент инерции поперечного се­чения стержня;

EI_min – жесткость поперечного сечения на изгиб (стержень изгибается в плоскости минимальной жёсткости),

l – длина стержня,

 – коэффициент приведения длины, учитывающий особенности закрепления стержня.

Эту задачу впервые решил академик Петербургской Академии наук Л. Эйлер в 1744 году, а выражение, определяющее величину критической силы стержня с шарнирно-опертыми концами назы­вается формулой Эйлера.

При шарнирном закреплении обоих концов стержня =1; для стержня с заделанными концами =0,5; для стержня с одним заделанным и другим свободным концом =2; для стержня с одним заделанным и другим шарнирно закрепленным концом =0,7.

Критическое напряжение (на основе формулы Эйлера)

где А – площадь поперечного сечения стержня,

 - гибкость стержня.

,например, для стали Ст3 (С235) _кр100.

i_min – минимальный радиус инерции В случае неприменимости формулы Эйлера критиче­ское напряжение, а значит, и критическая сила могут быть вычислены по эмпирическим формуле Ясинского. Для случая <_кр критическое напряжение вычисляется по эмпирической (полученной экспериментально) формуле Ясинского: 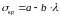коэффициенты "a" и "b" приведены в справочниках, например для Ст3: a=310МПа; b=1,14МПа.

Достаточно короткие стержни, для которых <₀=40 (для сталей) называются стержни малой гибкости. Такие стержни рассчитывают только на прочность.

В реальных условиях тонкий и длинный стержень не является идеальным. Как правило, уже до начала нагружения он имеет начальные неправильности (начальную погибь).

Рассмотрим шарнирно-опёртый по концам стержень (рис.9). В началь-ном состоянии ось стержня имеет форму полуволны синусоиды

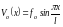^, (2)

где f₀ – стрела начального погиба.

При сжатии силой F стержень получает дополнительные перемещения

^. (3)

Здесь V – перемещение центра тяжести поперечного сечения в направлении оси y, или прогиб стержня; f – стрела прогиба. Форма упругой линии (3) подобна форме начальных неправильностей (2).

Величина прогиба определяется из решения дифференциального уравнения упругой линии

EI_minV"=-F(V+V_ο). (4)

Подставляя функции формы (2) и (3) в уравнение (4), находим

, (5)

где F_кр – критическая сила (1), рассчитанная при  =1. Выражение (5) носит название формулы Тимошенко.

l/2

f

f_o

x

l/2

y(V)

F

Рис. 2. Расчетная схема сжатого стержня

Следует иметь в виду, что поведение реального стержня (стержня с начальной погибью) при сжатии качественно отличается от поведения идеального стержня. Идеальный стержень при F  F_кр остаётся прямолиней-ным. Реальный же стержень уже при малых значениях силы F получает прогибы. Поэтому диаграмма “нагрузка – прогиб” получается нелинейной. По мере нарастания нагрузки прогибы растут. Причём, интенсивность прогибов зависит от начального погиба f₀: чем больше величина f₀, тем быстрее растут прогибы. При нагрузке, приближающейся к критической, прогибы быстро увеличиваются и при F = F_кр прогибы V→∞.

Экспериментальное исследование поведения гибкого стержня выпол-няется при помощи лабораторной установки М4, схема которой изображена на рис.10. Сжимающая сила создаётся при помощи съёмных грузов. Нагружение проводится ступенями с переменным шагом. На каждой ступени нагружения делается отсчёт по шкале прогибов.

3

9

6

4

5

10

11

2

7

9

10

11

12

8

1

Р

10

12

11

ис. . Схема лабораторной установки