9.6. Прогнозирование на основе динамических рядов

Прогнозирование – это определение значений признака в будущие периоды времени.

Процедура прогнозирования на основе тренда включает в себя следующие этапы:

1. расчет точечного прогноза;

2. расчет интервального прогноза;

3. оценка точности и надежности прогнозных значений.

Точечный прогноз представляет собой математическое ожидание значения признака в будущий момент времени. Вероятность точечного прогноза, т.е. того, что фактическое значение точно совпадет с прогнозным близка к нулю. Поэтому, практическое значение имеет интервальный прогноз, т.е. прогноз, который характеризуется определенной точностью и надежностью, при этом точность и надежность определяются базой прогноза.

Интервальный прогноз – это интервал, в который с определенной степенью вероятности попадет значение признака в прогнозный период или момент времени.

Интервальный прогноз можно рассчитать по формуле

,

где х_точ – точечный прогноз значения признака; m_xk – ошибка прогноза на t_k-й период или момент времени; t_Ст – коэффициент доверия Стьюдента.

Значение точечного прогноза определяется подстановкой номера прогнозного периода (или момента) времени в уравнение динамики и расчетом соответствующего ему значения признака. Например, для уравнения линейного тренда

,

где t_пр – номер прогнозного периода времени.

Ошибка прогноза учитывает ошибку тренда и ошибку колеблемости и рассчитывается по формуле

;

;

,

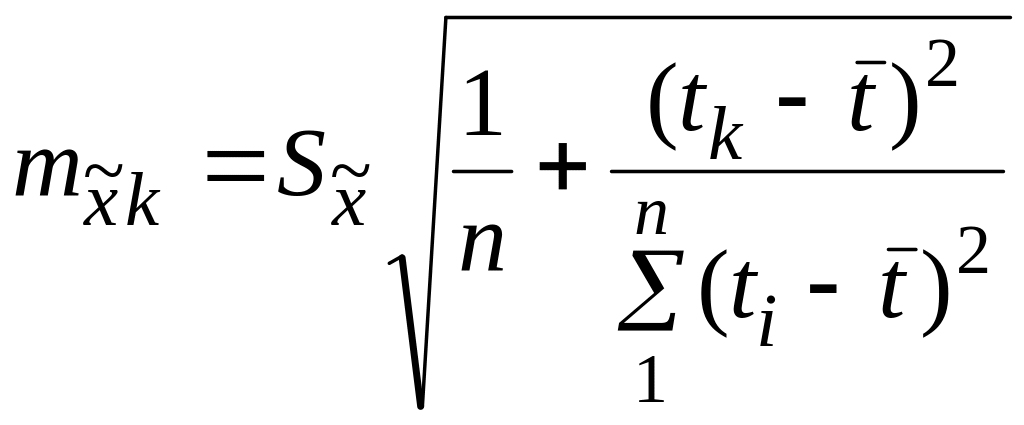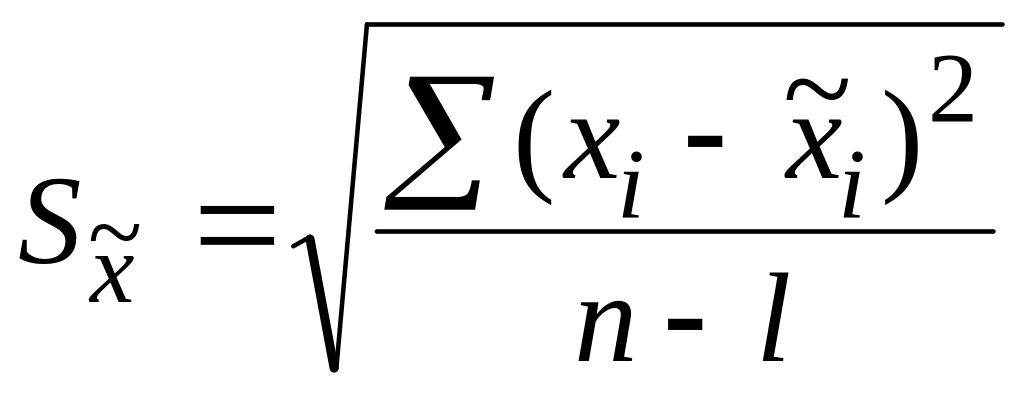где – ошибка линии тренда в t_k-м периоде; – среднее квадратичное отклонение фактических значений от тренда (ошибка колеблемости); n – база прогноза (число периодов в ряду динамики); t_k – номер прогнозного периода; – среднее значение из номеров периодов (моментов) времени в ряду динамики; – номера периодов времени в ряду динамики; – фактические значения уровней ряда динамики; – теоретические значения уровней ряда динамики; l – число потерянных степеней свободы (для линейного уравнения l = 2, для параболы l = 3).

Значение коэффициента доверия Стьюдента выбирается по таблице «Распределение Стьюдента» (приложение 2) по двум параметрам – степень значимости (обычно принимается равным 0,05) и число степеней свободы (n – l).

97