9.4. Методы выявления типа тенденции динамики. Расчет параметров тренда

Тренд – это аналитическое выражение, отражающее тенденцию динамики значений показателя. Тенденция динамики – это основное направление в изменении значений показателя с течением времени, обусловленное долговременно действующими факторами. Для выбора вида уравнения динамики (тренда) и расчета параметров можно использовать графический метод или метод наименьших квадратов.

Выявление типа тенденции динамики не является чисто математической задачей и требует предварительного качественного анализа. В ходе этого анализа необходимо ответить на вопросы: достаточно ли стабильными были условия развития изучаемого явления в прошедший период, не произошло ли существенных качественных изменений, каков характер действия основных факторов развития? Затем, следует сопоставить результаты последующего формального анализа с ответами на эти вопросы.

Описание графического метода и метода наименьших квадратов уже приводилось в теме 8 (п. 8.3). При определении уравнения динамики (тренда) в качестве факторного признака выступает время, в качестве результативного – уровень ряда динамики. В действительности изучаемый параметр изменяется, конечно же, не под влиянием времени, а под влиянием множества изменяющих свои значения с течением времени факторов, а время выступает лишь как обобщенный индикатор этих изменений. И внешне изменение показателя выглядит, как изменение под влиянием времени.

Графический метод определения тренда включает в себя следующие этапы:

1. нанести на поле координат (время – значение признака) точки, соответствующие значениям признака в каждый период времени;

2. на основе визуальной оценки расположения точек на поле координат провести прямую линию, наиболее точно отражающую тенденцию распределения точек (теоретически это может быть и парабола, и гипербола и т. д., но фактически, полагаясь на глазомер, отобразить криволинейные зависимости достаточно сложно);

3. выбрать на проведенной прямой две произвольные точки (для параболы – три точки) и, используя их координаты, записать и решить систему уравнений, определив, таким образом, параметры уравнения:

– система уравнений для прямой линии:

;

,

где (t₁, x₁) и (t₂, x₂) – координаты выбранных точек на прямой; а и b – неизвестные параметры уравнения;

– система уравнений для параболы:

;

;

,

где (t₁, x₁), (t₂, х₂) и (t₃, x₃) – координаты выбранных точек на линии тренда; а, b и с – неизвестные параметры уравнения;

– система уравнений для гиперболы:

;

,

где (t₁, x₁) и (t₂, х₂) – координаты выбранных точек на линии тренда; a и b – неизвестные параметры уравнения;

4. записать уравнение динамики, используя рассчитанные значения параметров a, b, c:

– для прямой линии ;

– для параболы ;

– для гиперболы .

Метод наименьших квадратов включает в себя следующие этапы:

1. рассчитать параметры уравнений по каждому из предполагаемых вариантов и записать соответствующие уравнения:

– система уравнений для расчета параметров уравнения прямой линейной зависимости

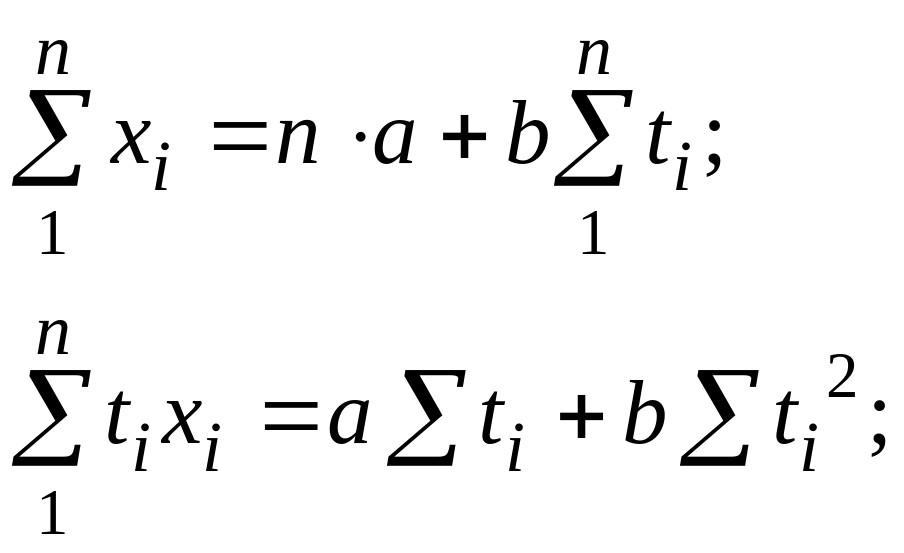
– система уравнений для расчета параметров уравнения параболы

– система уравнений для расчета параметров уравнения гиперболы

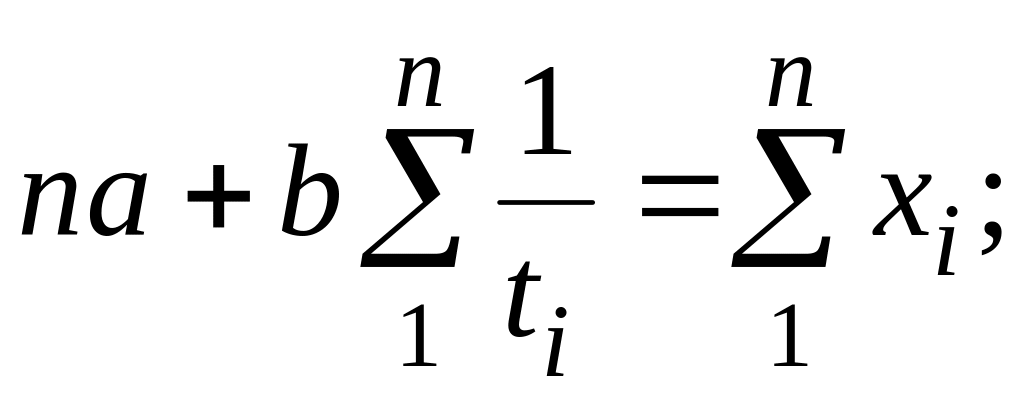
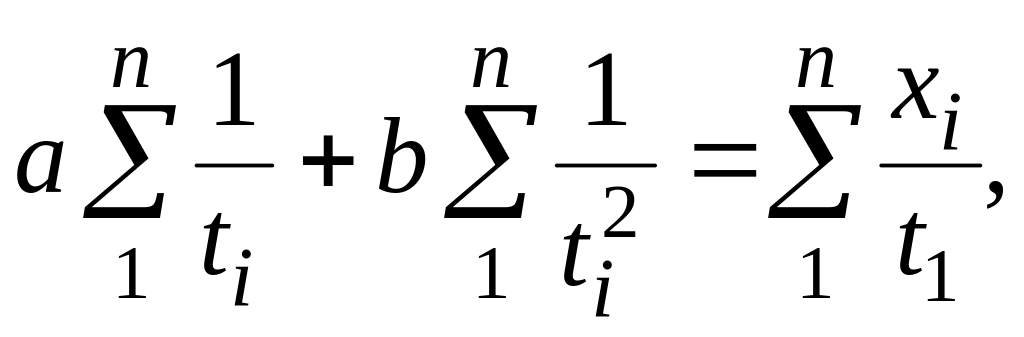
где t_i, x_i – соответственно периоды и уровни ряда динамики; а, b и с – неизвестные параметры соответствующего уравнения;

2. рассчитать сумму квадратов отклонений фактических значений признака от теоретических по каждому из предполагаемых вариантов и выбрать вариант уравнения, которому соответствует минимальное значение суммы квадратов отклонений;

3. записать уравнение динамики:

– для прямой линии ;

– для параболы ;

– для гиперболы .