13.Метод Зейделя чисельного розв’язання слар.

Метод простої ітерації досить повільно збігається. Для його прискорення існує метод Зейделя. Суть його в тому, що при обчисленні компонентів х_і^(к+1)вектора невідомих на (k+1)-ій ітерації використовуються х₁^(к+1), х₂^(к+1),...,х_і-1^(к+1), уже обчислені на (k+1)-ій ітерації. Значення інших компонентів беруться з попередньої ітерації. Так само, як і у методі простих ітерацій, будується еквівалентна СЛАР (3.26) і за початкове наближення береться вектор правих частин X⁰=(β₁,β₂,…, β_n)^*.

Тоді метод Зейделя для пошуку наближення Х^(к+1) має вигляд

Із цієї системи бачимо, що Х^k+1=β+BХ^k+1+CХ^k , де В - нижня трикутна матриця з діагональними елементами, що дорівнюють нулю, а C - верхня трикутна матриця з діагональними елементами, відмінними від нуля, α=В+С. Отже, ,

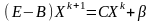звідки .

Таким чином, метод Зейделя є методом простих ітерацій з матрицею правих частин =(E-B)^-1C і вектором правих частин (E-B)^-1β, й, отже, збіжність і похибку методу Зейделя можна досліджувати за допомогою формул, виведених для методу простих ітерацій, у яких замість матриці підставлена матриця (E-B)^-1C, а замість вектора правих частин - вектор (E-B)^-1β. Для практичних обчислень важливо, що як достатні умови збіжності методу Зейделя можуть бути використані умови, наведені вище для методу простих ітерацій ( або, якщо використовується еквівалентна СЛАР у формі (3.1), -діагональна перевага матриці А). У випадку виконання цих умов для оцінки похибки на k -ій ітерації можна використати вираз

Відзначимо, що, як і метод простих ітерацій, метод Зейделя може збігатися й при порушенні умови .

14.Метод Гаусса чисельного розв’язання слар.

Цей метод базується на приведенні шляхом еквівалентних перетворень вихідної системи (3.1) до вигляду з верхньою трикутною матрицею.

с₁₁x₁+ c₁₂x₂ + … + c_1nx_n = d₁

0 + c₂₂x₂ + … + c_2nx_n = d₂

................................................ (3.3)

0 + … 0+ c_n-1,n-1x_n-1 + c_n-1,nx_n = d_n-1

0 + 0 + +0 + c_nnx_n = d_n

Тоді з останнього рівняння відразу визначаємо . Підставляючи його в попереднє рівняння, знаходимо x_n-1 і т.д. Загальні формули для отримання розв’язку мають вигляд

(3.4)

Запишемо загальні формули процесу. Нехай проведене виключення коефіцієнтів з k-1 стовпця. Тоді залишилися такі рівняння з ненульовими елементами нижче головної діагоналі:

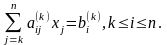(3.5)