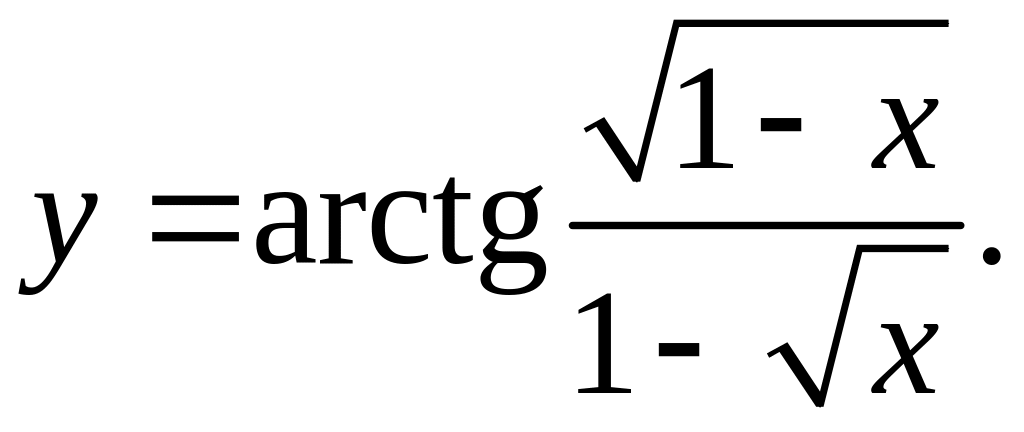- •5. Диференціальне числення функції
- •5.1. Похідна функції, її геометричний і фізичний зміст.
- •5.2. Основні правила диференціювання функцій
- •5.3. Похідні вищих порядків
- •5.4. Диференціал функції
- •5.5. Диференціювання за допомогою пакету Maxima
- •5.6. Наближені обчислення за допомогою диференціала
- •5.7. Дослідження функції за допомогою похідних
- •5.8. Визначення максимуму і мінімуму функції за допомогою пакету Maxma
5. Диференціальне числення функції
одній змінній.
5.1. Похідна функції, її геометричний і фізичний зміст.
Визначення. Похідній функції f(x) в точці х = х0 називається границя відношення приросту функції в цій точці до приросту аргументу, якщо він існує.
![]() .
(5.1)
.
(5.1)
 в
в
f(x)
f(x0 +(x) P
f
f(x0) M
x
0 x0 x0 + (x x
Рис. 5.1.
Хай
f(x)
визначена на деякому проміжку (а,
b).
Тоді
![]() тангенс кута нахилу січної МР до графіка
функції.
тангенс кута нахилу січної МР до графіка
функції.
![]() ,
,
де ( - кут нахилу дотичної до графіка функції f(x) в точці (x0, f(x0)).
Кут між кривими може бути визначений як кут між дотичними, проведеними до цих кривих в якій - набудь точці.
Рівняння
дотичної до кривої:
![]() .
(5.2)
.
(5.2)
Рівняння
нормалі до кривої:
![]() .
(5.3)
.
(5.3)
Фактично похідна функції показує як би швидкість зміни функції, як змінюється функція при зміні змінній.
Фізичний зміст похідної функції f(t), де t - час, а f(t) - закон руху – миттєва швидкість руху.
Відповідно, друга похідна функції - швидкість зміни швидкості, тобто прискорення.
Функція у = f(x), що має похідну в кожній точці інтервалу (а, b), називається такою, що диференціюється в цьому інтервалі. Відповідно операція знаходження похідної функції називається диференціюванням.
Розглянемо основні властивості функцій, що диференціюються.
Теорема 1 (необхідна умова існування похідної) Якщо функція f(x) має похідну в точці х0, то вона безперервна в цій точці.
Теорема 2. Якщо функція у = f(x) на інтервалі (а, b) монотонна і має в довільній точці х цього інтервалу похідну
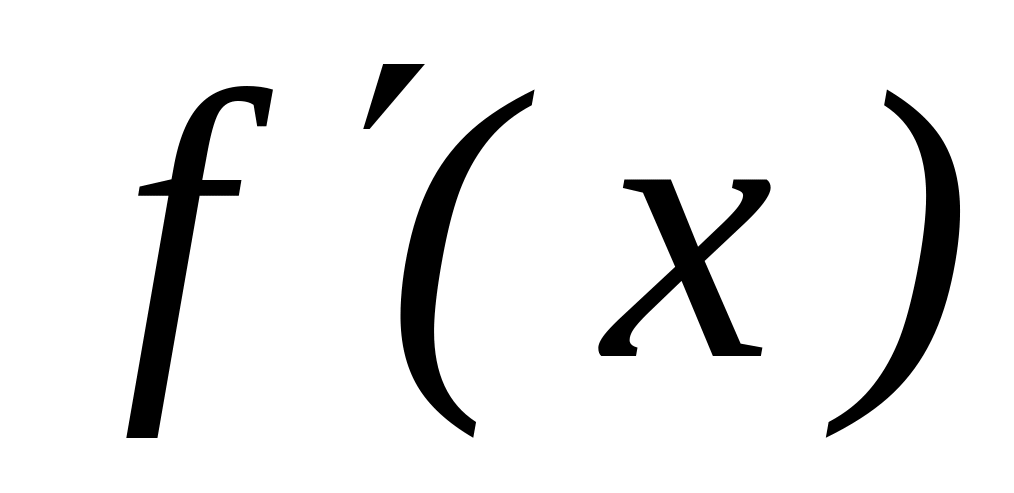 не рівною нулю, то зворотна функція х
= φ (у)
також має похідну
не рівною нулю, то зворотна функція х
= φ (у)
також має похідну
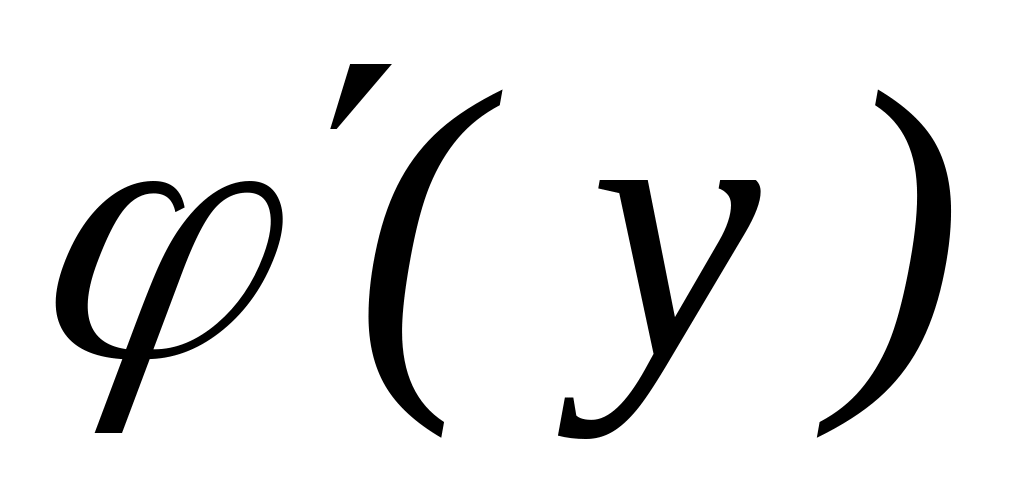 у відповідній точці і рівна
у відповідній точці і рівна
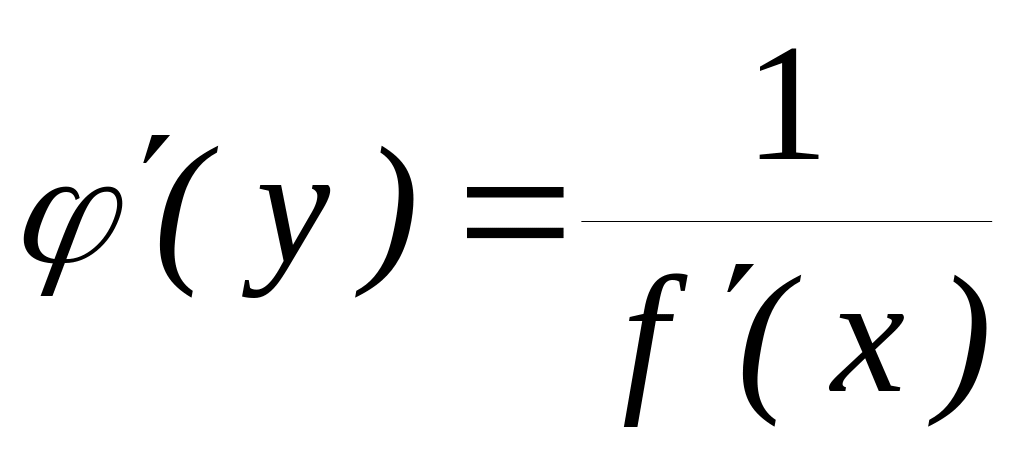 .
(5.4)
.
(5.4)
Отже, похідна зворотної функції дорівнює зворотній величині похідної даної функції.
5.2. Основні правила диференціювання функцій
На практиці знаходження похідної функції часто пов'язане з певними труднощами, тому зручно користуватися надалі наступними правилами диференціювання.
Хай функції u = u (x) і v = v(x) – диференційовані в точці х . а C – постійна величина (C = const). Мають місце наступні правила:
1)
![]() ;
;
2)
![]() ;
;
(u ( v)( = u( ( v( ;
(u(v)( = u(v( + u((v ;
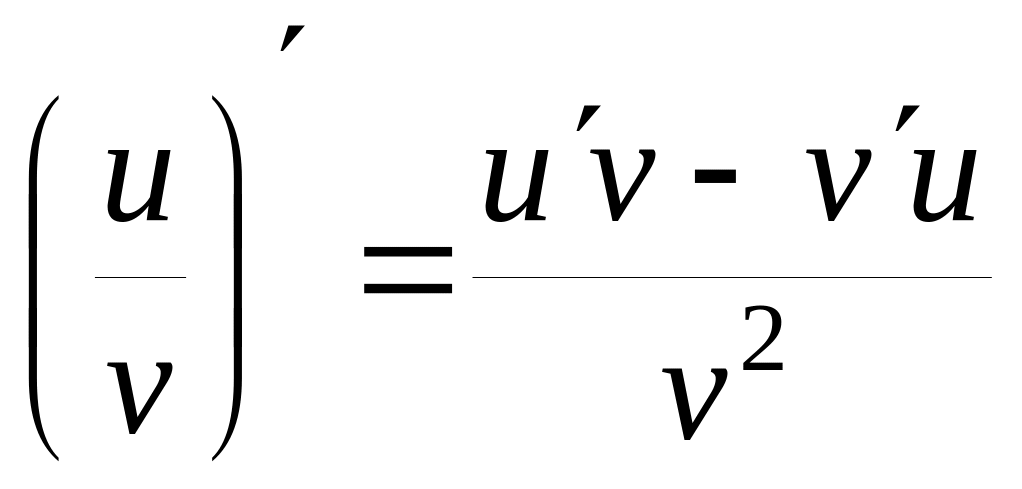 ,
якщо
v ( 0 .
,
якщо
v ( 0 .
Ці правила можуть бути легко доведені на основі теорем про границі.
Нижче наводиться таблиця похідних елементарних функцій:
-
1) С( = 0
9)
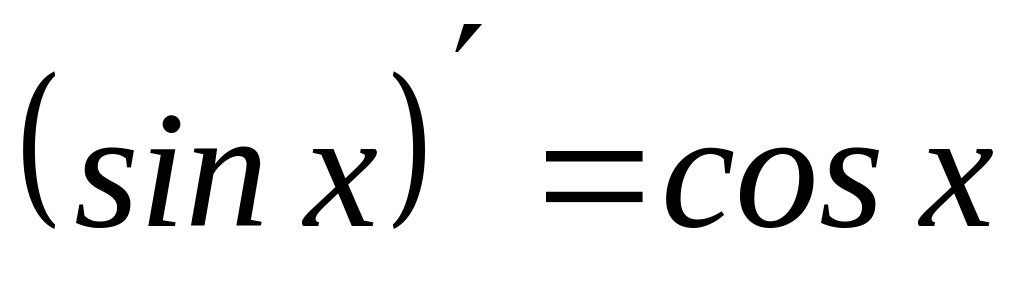
2) ( xm )( = m xm-1
10)

3)
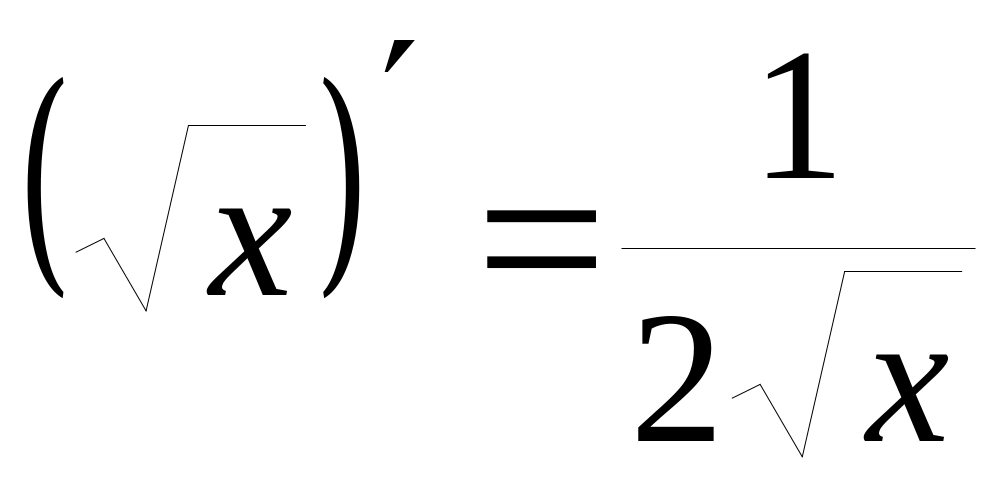
11)
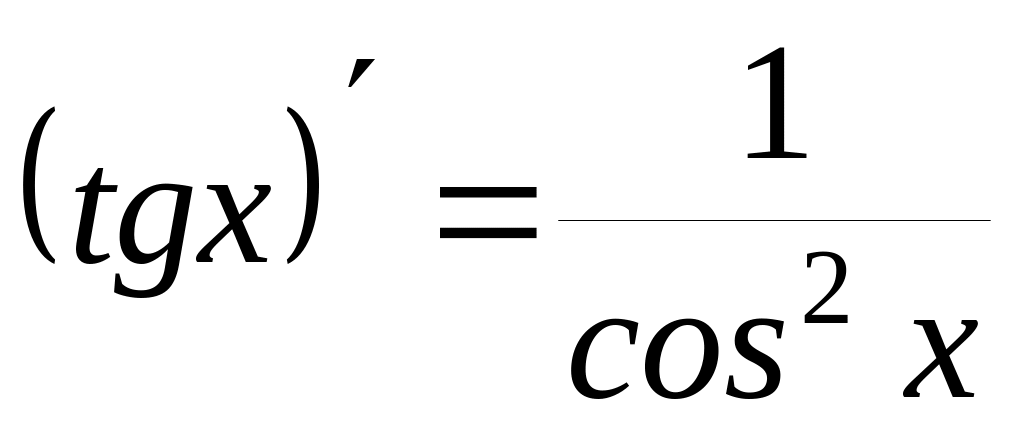
4)
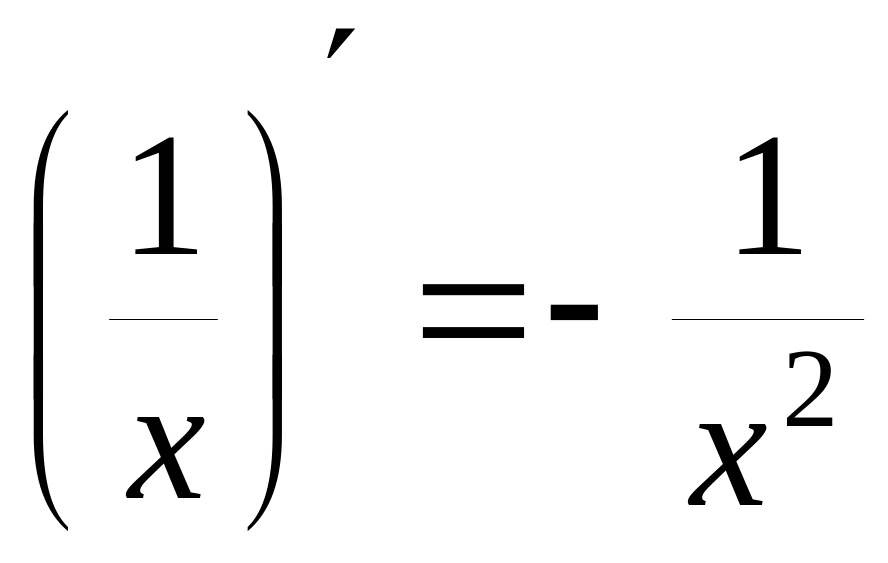
12)
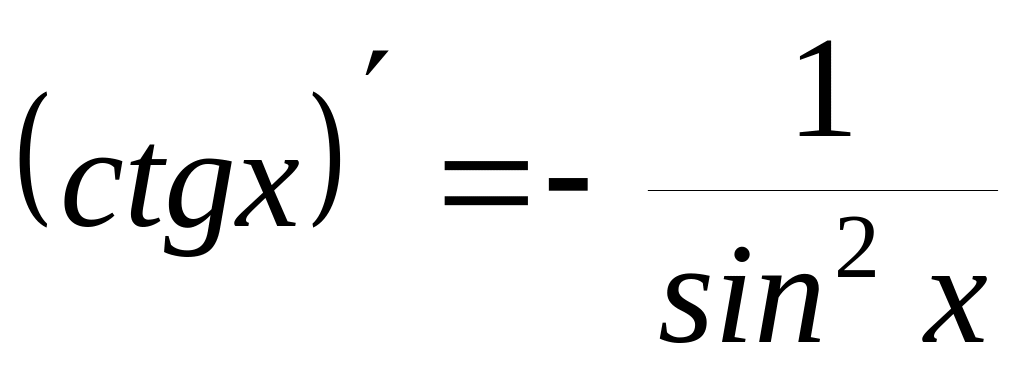
5)

13)
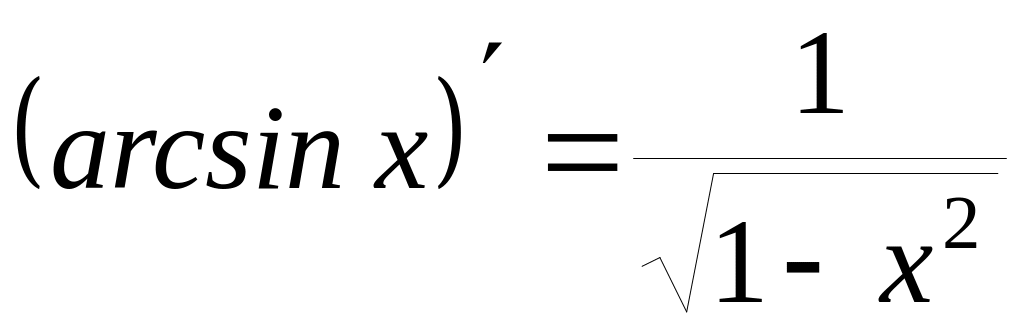
6)
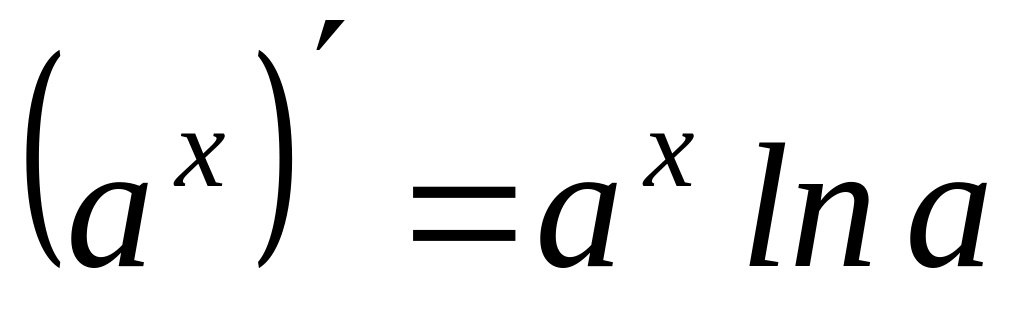
14)
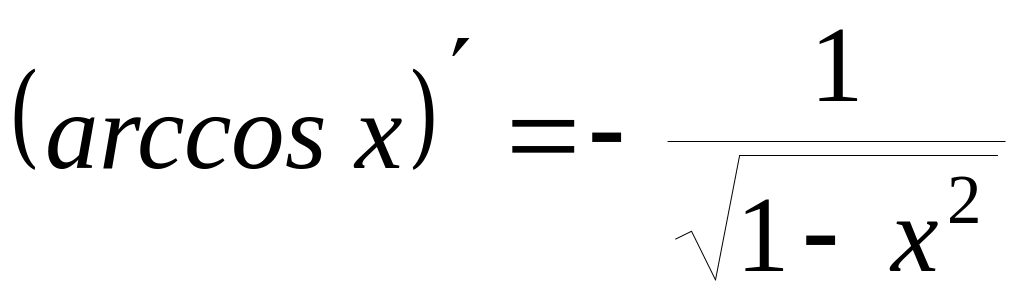
7)
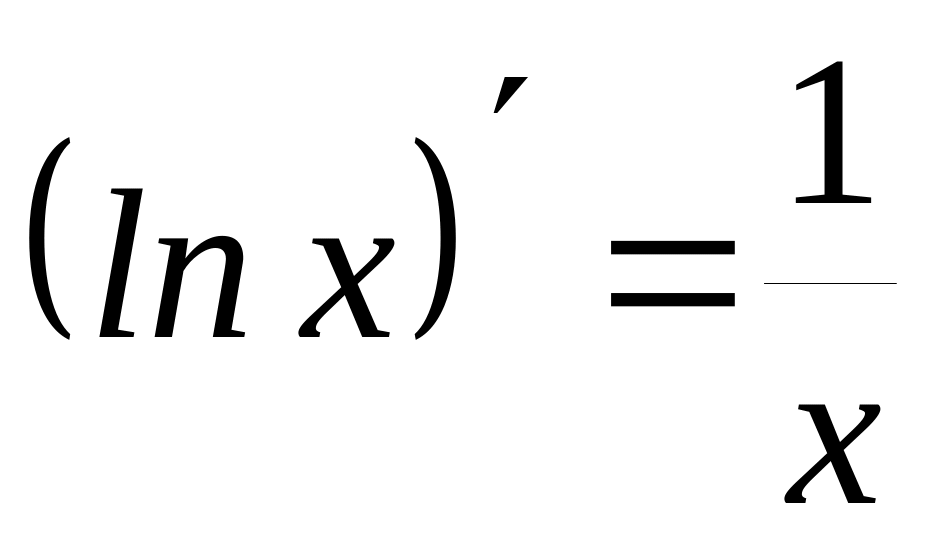
15)

8)

16)
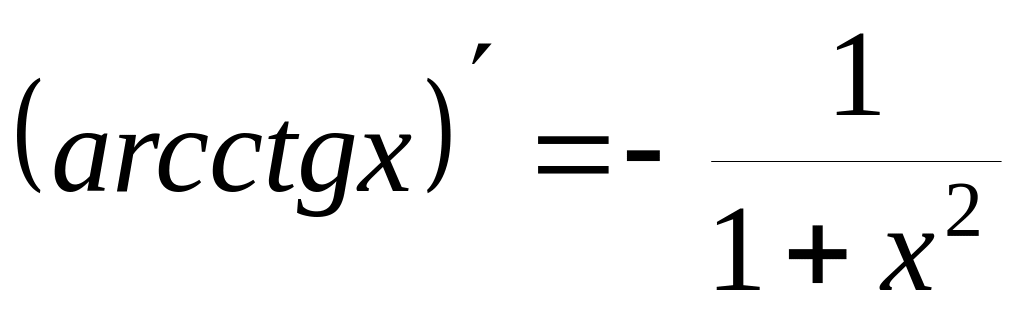
Похідна складної функції.
Теорема. Хай функції y = f(u) і u = g(x) диференційовані у відповідній точці, причому область значень функції g(x) входить в область визначення функції f.
Тоді
![]() . (5.5)
. (5.5)
Доведення.
![]() ,
,
![]()
(з урахуванням того, що якщо x0, то u0, тому u = g(x) – безперервна функція)
Тоді
![]() .
Теорема доведена.
.
Теорема доведена.
Приклади. Знайти похідну
1)
![]()
![]()
2)
![]()
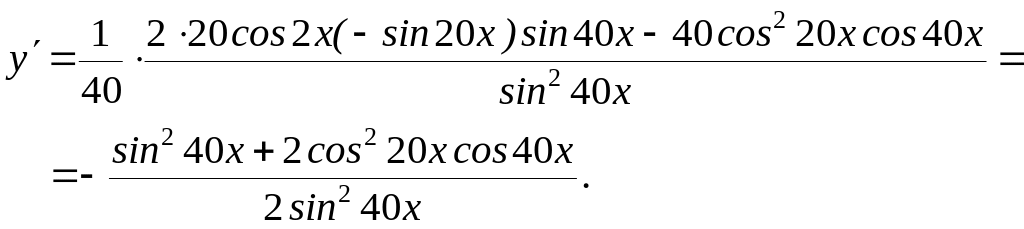
Логарифмічне диференціювання.
На практиці у ряді випадків для знаходження похідної функції зручно спочатку прологарифмувати цю функція, а потім результат продиференціювати. Така подвійна процедура називається логарифмічним диференціюванням. Метод логарифмічного диференціювання зручно застосовувати для знаходження похідних складних, особливо показникових функцій, для яких безпосереднє обчислення похідної з використанням правил диференціювання представляється трудомістким.
Розглянемо
функцію
![]() .
.
Тоді
(lnx)=
![]() ,
оскільки
,
оскільки
![]() .
Враховуючи отриманий результат, можна
записати
.
Враховуючи отриманий результат, можна
записати
![]() . Тут відношення
. Тут відношення
![]() називається логарифмічній похідній
функції f(x).
називається логарифмічній похідній
функції f(x).
В
результаті
![]() . (5.6)
. (5.6)
Приклади. 1) Похідна степенево-показової функції
![]() .
(5.7)
.
(5.7)
2)
![]() ,
,
![]()
3)
![]() ,
,
![]() .
.
Функція, задана параметрично
Хай залежність між аргументом х і функцією у задана в параметричному вигляді
![]() ,
де t – параметрична змінна.
,
де t – параметрична змінна.
Знайдемо похідну, вважаючи, що функції x(t) і у(t) мають похідні і крім того x(t) має зворотну функцію t = φ(х). За правилом диференціювання зворотної функції (5.4)
![]() .
.
За
правилом диференціювання складної
функції (5.5) маємо:
![]() ,
в результаті,
,
в результаті,
![]() тобто
тобто
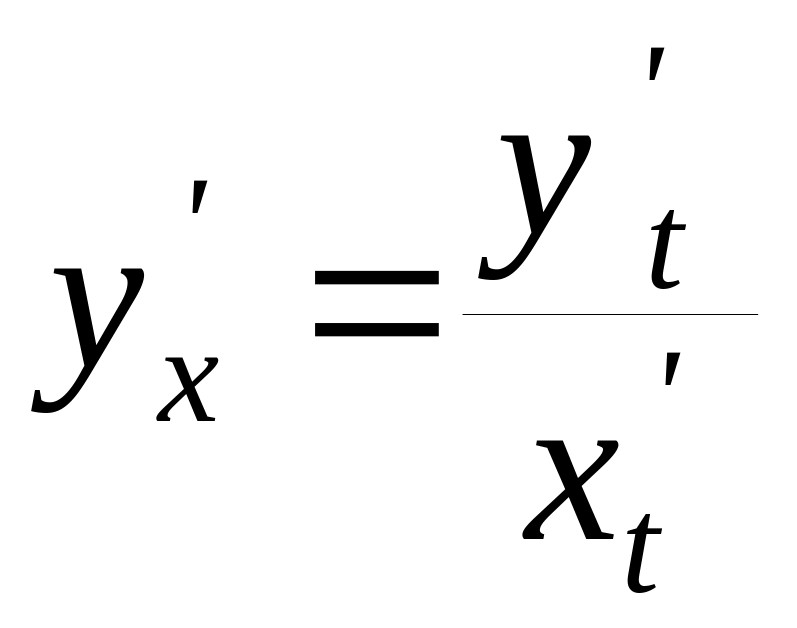 . (5.8)
. (5.8)
Отримана
формула (5.8) дозволяє знаходити похідну
![]() якщо залежність у
від х
задана параметрично.
якщо залежність у
від х
задана параметрично.
Приклад.
![]()
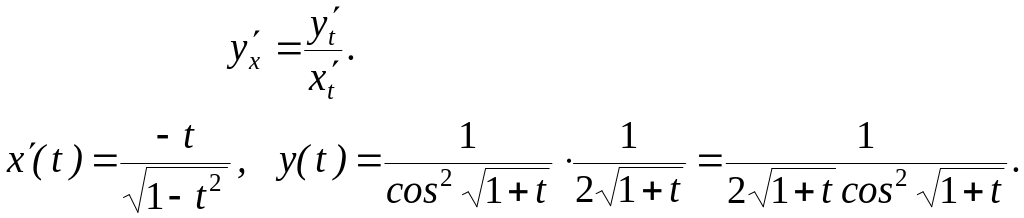
![]()
Приклади для самостійного розв’язання
Знайти похідну
1)
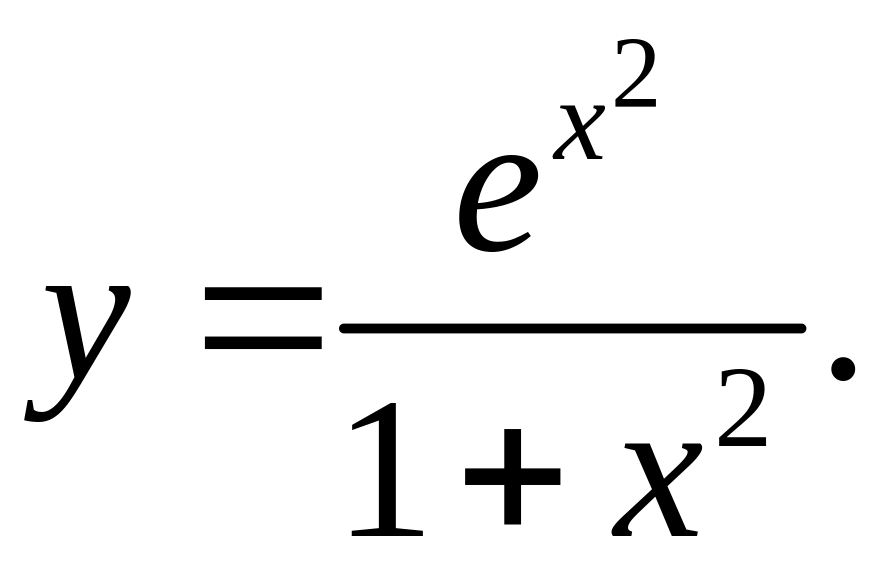 2)
2)
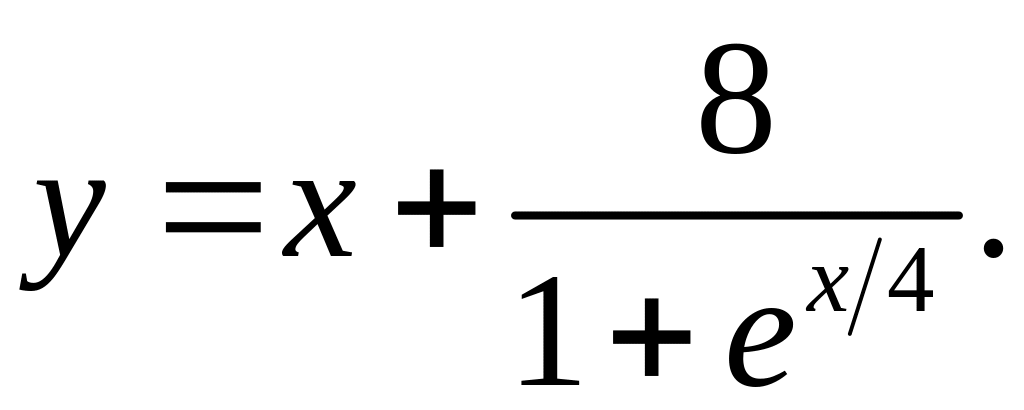 3)
3)
![]() 4)
4)
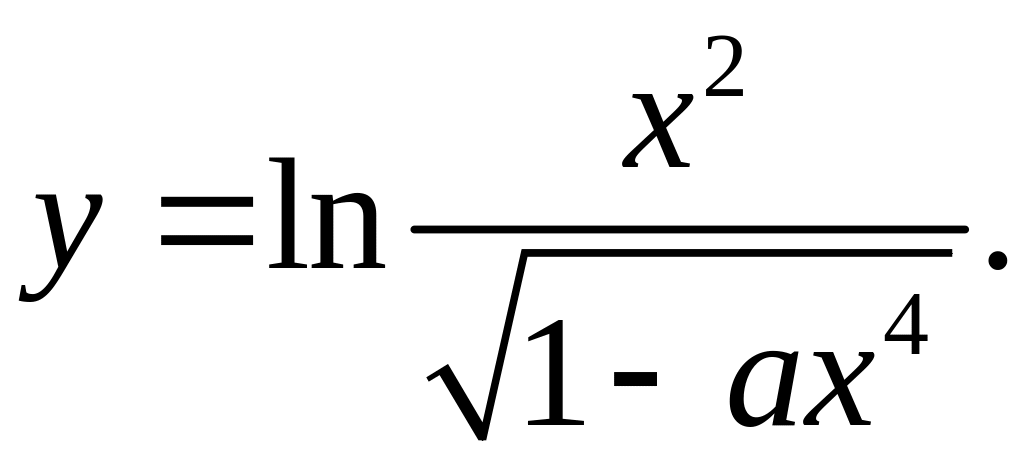
5)
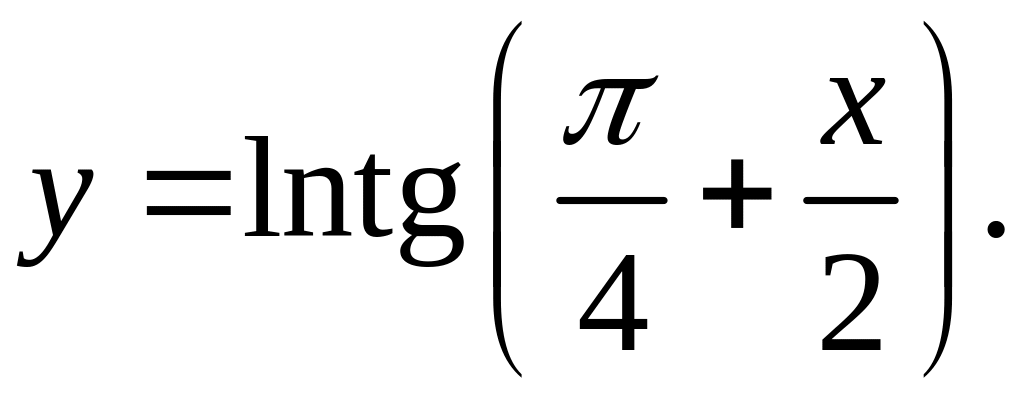 6)
6)
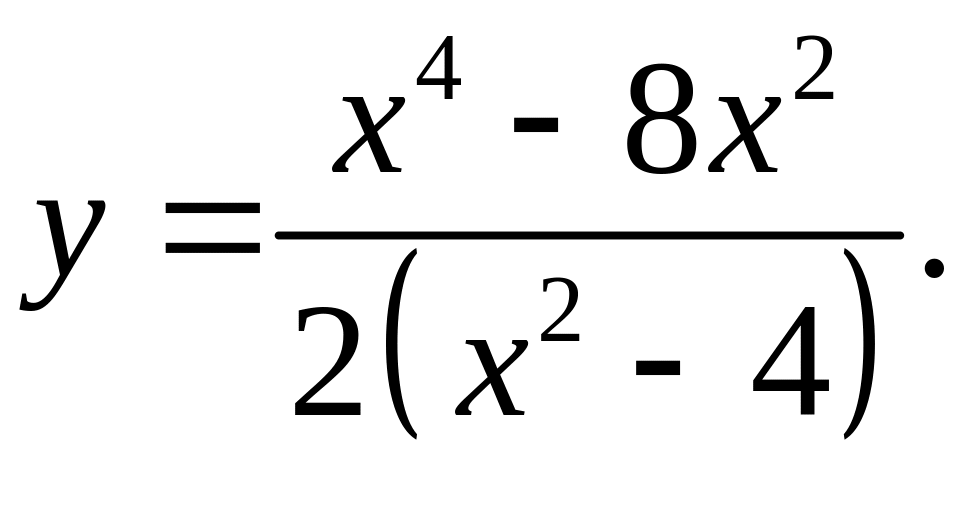 7)
7)
 8)
8)