8.3. Розвинення функції в ряд Тейлора в Maxima
У Maxima існує спеціальна функція, що дозволяє обчислювати ряди і многочлени Тейлора taylor.
Синтаксис застосовності функції taylor
taylor(expr, x, a, n),
тут expr - розвинений в ряд вираз;
a - значення x, в околиці якого виконується розвинення (по степеням x − a);
n - параметр, що вказує на порядок розвинення і представлений цілим пози-
тивним числом.
Якщо a вказується просто у вигляді імені змінної, то виробляється обчислення ряду і многочлена Маклорена.
Приклад 1. Знайти многочлен Тейлора 8-ій степені експоненціальної функції ex на початку координат
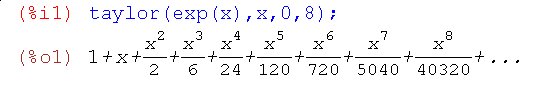
Разом з командою taylor для розвинення функцій і виразів в ряди використується команда powerseries (будується розкладання для заданого виразу по змінній x в околу a). Результатом виконання команди powerseries може бути побудова її ряду Тейлора в загальній формі, наприклад:
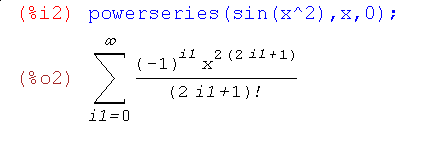
Ряди можна складати, віднімати, множити і ділити один на одного, при цьому точність розвинення враховується автоматично, наприклад
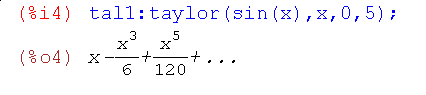
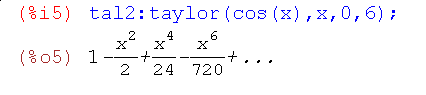
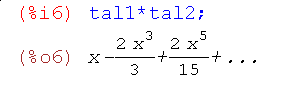
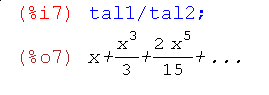
тобто розкладання йде до п'ятого порядку (точність першого ряду).
Завдання для самостійного розв‘язку
Розкласти функцію в ряд Тейлора по степеням х в точці х = 1 до шостого порядку
8.49.
Відповідь:
8.50.
. Відповідь:
8.51.
Відповідь:
8.52.
Відповідь:
8.53. Відповідь:
8.54.
Відповідь:
8.55.
Відповідь:
8.56. . Відповідь:
8.57.
. Відповідь:
8.58.
Відповідь:
8.59.
. Відповідь:
8.60.
.
Відповідь:
8.61.
Відповідь:
8.62.
Відповідь:
8.63.
Відповідь:
8.64.
Відповідь:
9. Література
1. Д.Т. Письменный. Конспект лекцій по высшей математике. М.: Айрис-пресс, 2010. – 608 с.
2. Вища математика. Підручник. За редакцією Шинкарика М.І. Видавництво Карп’юка, Тернополь. 2003. 483 с.
3. Курс вищої математики. Навчальний посібник. За редакцією Кузаконь В.М. Одеса: Видавництво ОНАХТ. 2012. 256 с.
4. В.Ю.Клепко, В.Л. Голець. Вища математика в прикладах і задачах: Навчальний посібник. К.: Центр учбової літератури, 2009.- 594 с.
