
8. Ряди
8.1. Числові ряди. Основні визначення.
Нехай a1 , a2, …, aп , … - числова послідовність. Сума членів послідовності
a1
+ a2+…+
aп
+
…
=
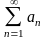 (8.1)
(8.1)
називається числовим рядом.
Кінцеві
суми
 =
=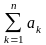 ,
n
= 1,2,3,…
,
n
= 1,2,3,…
називаються частковими сумами ряду (8.1).
Якщо
існує кінцева границя послідовності
часткових
сум
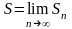 , то ряд називається збіжним,
а число S
- сумою
ряду.
, то ряд називається збіжним,
а число S
- сумою
ряду.
=
S
або
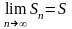 .
(8.2)
.
(8.2)
Якщо
не існує кінцевої границі послідовності
часткових сум
 ,
то ряд називається розбіжним.
,
то ряд називається розбіжним.
Ознаки збіжності ряду
Необхідна
ознака збіжності ряду.
Якщо ряд
збіжний,
то необхідно, щоб загальний член an
прямує до нуля, тобто
 .
.
Достатня
умова розбіжності числового ряду.
Якщо
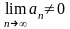 або ця границя не існує, то ряд розбігається.
або ця границя не існує, то ряд розбігається.
Достатні ознаки збіжності позитивних числових рядів.
Ознаки порівняння з «еталонним» рядом:
Нехай дано два позитивні ряди і
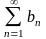 (an,
bn
0 )
і виконується нерівність an
bn
при будь-якому n,
тоді із збіжності ряду
виходить
збіжність ряду
,
а з розбіжності ряду
виходить
розбіжність ряду
.
(an,
bn
0 )
і виконується нерівність an
bn
при будь-якому n,
тоді із збіжності ряду
виходить
збіжність ряду
,
а з розбіжності ряду
виходить
розбіжність ряду
.Якщо для позитивних рядів і існує кінцева і відмінна від нуля
границя
 ,
то ряди
і
одночасно
збігаються
або розбігаються.
,
то ряди
і
одночасно
збігаються
або розбігаються.
«Етолонні» ряди:
Розбіжний гармонійний ряд
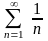 ;
;Узагальнений гармонійний ряд
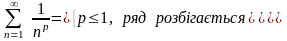 ;
;геометричний ряд
 .
.
Нехай дано два позитивні ряди і (an, bn 0 ) і виконується нерівність
 при будь-якому n,
тоді із збіжності ряду
виходить
збіжність ряду
,
а із розбіжності ряду
виходить
розбіжність ряду
.
при будь-якому n,
тоді із збіжності ряду
виходить
збіжність ряду
,
а із розбіжності ряду
виходить
розбіжність ряду
.
Приклади:
1.
Дослідити
на збіжність ряд

Оскільки
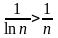 ,
а гармонійний ряд
,
а гармонійний ряд
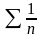 розбігається, то розбігається також і
ряд
розбігається, то розбігається також і
ряд
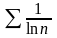 .
.
2.
Дослідити
на збіжність ряд

Оскільки
 ,
а ряд
,
а ряд
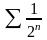 збігається (як убиваюча геометрична
прогресія), то ряд
збігається (як убиваюча геометрична
прогресія), то ряд
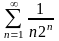 теж збігається.
теж збігається.
3.
Дослідити
на збіжність ряд
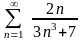 .
.
Порівнюємо
цей ряд із збіжним рядом
 ,
загальними членами цих рядів
,
загальними членами цих рядів
являються
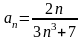 і
і
 .
Застосовуємо граничну ознаку порів-няння
.
Застосовуємо граничну ознаку порів-няння
 . Ряд збігається.
. Ряд збігається.
4.
Дослідити
на збіжність ряд
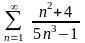 .
.
Порівнюємо
цей ряд із розбіжним рядом
,
застосовуємо граничну ознаку порівняння
 . Ряд розбігається.
. Ряд розбігається.
5.
Дослідити
на збіжність ряд
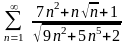 .
.
Порівнюємо
цей ряд із розбіжним рядом
,
застосовуємо граничну ознаку порівняння
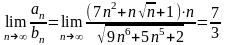 . Ряд розбігається.
. Ряд розбігається.
Ознака Даламбера
Нехай
для позитивного ряду
існує границя
 .
Тоді ряд збігається при l
< 1 і розбігається при
l
>1.
.
Тоді ряд збігається при l
< 1 і розбігається при
l
>1.
Приклади:
1.
Дослідити
на збіжність ряд
 .
.
За
ознакою Даламбера
 . Ряд збігається.
. Ряд збігається.
2.
Дослідити
на збіжність ряд
 .
.
За
ознакою Даламбера
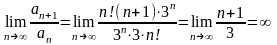 . Ряд
розбігається.
. Ряд
розбігається.
3.
Дослідити
на збіжність ряд
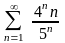
За
ознакою Даламбера
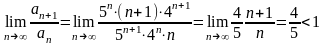 .
Ряд
збігається.
.
Ряд
збігається.
4.
Дослідити
на збіжність ряд
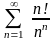 .
.
За
ознакою Даламбера
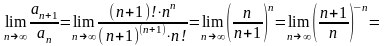
=
 .
Ряд збігається.
.
Ряд збігається.
Радикальна ознака Коші
Нехай
для позитивного ряду
(an
≥
0)
існує границя
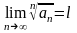 .
.
Тоді справедливі наступні твердження:
а) якщо, l < 1 те цей ряд збігається;
б) якщо, l > 1 те цей ряд розбігається.
Приклад.
Дослідити
на збіжність ряд
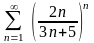 .
.
Розв‘язок. За радикальною ознакою Коші
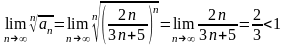 .
Ряд збігається.
.
Ряд збігається.
Інтегральна ознака Коші
Якщо
члени позитивного ряду
можуть
бути представлені як числові значення
деякої безперервної монотонно спадною
на проміжку [1,+∞) функції f(x)
так, що
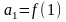 ,
,
 ,
…,
,
…,
 ,…,
то
ряд
і
невласний інтеграл
,…,
то
ряд
і
невласний інтеграл
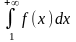 збігаються або розбігаються одночасно.
збігаються або розбігаються одночасно.
Приклади:
