
- •5. Невизначний інтеграл
- •5.1. Первісна функція і невизначений інтеграл
- •5.2.Основні методи інтегрування
- •1). Тригонометричні підстановки
- •2). Підстановки Ейлера
- •3). Метод невизначених коефіцієнтів.
- •5.3. Задачі для самостійного розв‘язку
- •5.4. Обчислення невизначених інтегралів в середовищі Maxima
1). Тригонометричні підстановки
Інтеграл
вигляду
 підстановкою
підстановкою
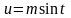 або
або
 зводиться до інтеграла від раціональної
функції відносно sin
t
або cos
t.
зводиться до інтеграла від раціональної
функції відносно sin
t
або cos
t.
Приклад.


Інтеграл
вигляду
 підстановкою
підстановкою
 або
або
 зводиться до інтеграла від раціональної
функції відносно sin
t
і cos
t.
зводиться до інтеграла від раціональної
функції відносно sin
t
і cos
t.
Приклад:


Інтеграл
вигляду
 підстановкою
підстановкою
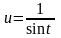 або
або
 зводиться до інтеграла від раціональної
функції відносно sin
t
або cos
t.
зводиться до інтеграла від раціональної
функції відносно sin
t
або cos
t.
Приклад.

2). Підстановки Ейлера
1.
Якщо а
> 0, то інтеграл вигляду
 раціоналізується підстановкою
раціоналізується підстановкою
 .
.
Якщо а < 0 і с > 0, то інтеграл вигляду раціоналізується підстановкою
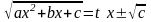 .
.
Якщо
а
< 0, а підкорінний вираз розкладається
на дійсні множники a
(x
– x1)(x
– x2),
те інтеграл вигляду
раціоналізується підстановкою
 .
.
3). Метод невизначених коефіцієнтів.
Розглянемо інтеграли наступних трьох типів:

де P(x) – многочлен, n – натуральне число.
Причому інтеграли II і III типів можуть бути легко приведені до вигляду інтеграла I типа.
Інтеграли типа I можна обчислювати, користуючись формулою
 ,
,
де Q(x) - деякий многочлен, степінь якого нижча за степінь многочлена P(x), а ( - деяка постійна величина.
Для
знаходження невизначених коефіцієнтів
многочлена Q(x),
степінь якого нижча за степінь многочлена
P(x),
диференціюємо обоє частини даного
виразу, потім умножають на
 і, порівнюючи коефіцієнти при однакових
степенях х,
визначають λ
і коефіцієнти многочлена Q(x).
і, порівнюючи коефіцієнти при однакових
степенях х,
визначають λ
і коефіцієнти многочлена Q(x).
Приклади.
 .
.
Диференціюємо цей вираз, потім помножимо на і згрупуємо коефіцієнти при однакових степенях х.

 =
=
 =
=
=
 .
.
Прирівняємо коефіцієнти при однакових степенях х

Таким чином,
 =
=
=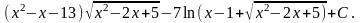










 ,
,
 .
Звідки
.
Звідки

Отже
 .
.
Інтегрування
диференціальних біномів. Розглядається
інтеграли
типа
 , де а,b
– дійсні числа; m,
n,
і p
– раціональні числа.
, де а,b
– дійсні числа; m,
n,
і p
– раціональні числа.
Як було доведено Чебишевим П.А., інтеграл від диференціального бінома може бути виражений через елементарні функції лише в наступних трьох випадках:
Якщо р – ціле число, то інтеграл раціоналізується за допомогою підстановки
 ,
де λ - спільний знаменник m
і n.
,
де λ - спільний знаменник m
і n.Якщо
 - ціле число, то інтеграл раціоналізується
підстановкою
- ціле число, то інтеграл раціоналізується
підстановкою
 ,
де s
– знаменник числа р.
,
де s
– знаменник числа р.
Якщо
 - ціле число, то використовується
підстановка
- ціле число, то використовується
підстановка , де s
– знаменник числа р.
, де s
– знаменник числа р.
Приклад.
Знайти інтеграл I
=
 .
.
Оскільки
диференціальний біном -

то
 . Тому робимо підстановку
. Тому робимо підстановку

тоді
 ,
,
 . В результаті
. В результаті
I
=
=

=
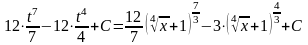 .
.
5.3. Задачі для самостійного розв‘язку
Знайти інтеграли
а). Безпосереднє інтегрування
5.1.
 Відповідь:
5.2.
Відповідь:
5.2.
 Відповідь:
Відповідь:
5.3.
 Відповідь:
5.4.
Відповідь:
5.4.
 Відповідь:
Відповідь:
5.5.
 Відповідь:
5.6.
Відповідь:
5.6.
 Відповідь:
Відповідь:
5.7.
 Відповідь:
5.8.
Відповідь:
5.8.
 Відповідь:
Відповідь:
5.9.
 Відповідь:
5.10.
Відповідь:
5.10.
 Відповідь:
Відповідь:
5.11.
 Відповідь:
5.12.
Відповідь:
5.12.
 Відповідь:
Відповідь:
5.13.
 Відповідь:
5.14.
Відповідь:
5.14.
 Відповідь:
Відповідь:
5.15.
 Відповідь:
5.16.
Відповідь:
5.16.
 Відповідь:
Відповідь:
5.17.
 Відповідь:
5.18.
Відповідь:
5.18.
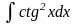 Відповідь:
Відповідь:
5.19.
 Відповідь:
5.20.
Відповідь:
5.20.
 Відповідь:
Відповідь:
5.21.
 Відповідь:
5.22.
Відповідь:
5.22.
 Відповідь:
Відповідь:
5.23.
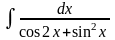 Відповідь:
5.24.
Відповідь:
5.24.
 Відповідь:
Відповідь:
5.25.
Відповідь:
5.26.
 Відповідь:
Відповідь:
5.
27.
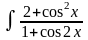 Відповідь:
5.28.
Відповідь:
5.28.
 Відповідь:
Відповідь:
b). Інтегрування методом підстановки
5.29.
 Відповідь:
5.30.
Відповідь:
5.30.
 Відповідь:
Відповідь:
5.31.
 Відповідь:
5.32.
Відповідь:
5.32.
 Відповідь:
Відповідь:
5.33.
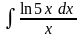 Відповідь:
5.34.
Відповідь:
5.34. Відповідь:
Відповідь:
5.35.
 Відповідь:
5.36.
Відповідь:
5.36.
 ;
Відповідь:
;
Відповідь:
5.37.
 ;
Відповідь:
5.38.
;
Відповідь:
5.38.
 ;
Відповідь:
;
Відповідь:
5.39.
 ;
Відповідь:
5.40.
;
Відповідь:
5.40.
 ;
Відповідь:
;
Відповідь:
5.41.
 ;
Відповідь:
5.42.
;
Відповідь:
5.42.
 ;
Відповідь:
;
Відповідь:
5.43.
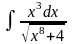 ;
Відповідь:
5.44.
;
Відповідь:
5.44.
 ;
Відповідь:
;
Відповідь:
5.45.
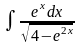 ;
Відповідь:
5.4
6.
;
Відповідь:
5.4
6.
 ;
Відповідь:
;
Відповідь:
5.47.
 ;
Відповідь:
5.48.
;
Відповідь:
5.48.
 ;
Відповідь:
;
Відповідь:
5.49.
 ;
Відповідь:
5.50.
;
Відповідь:
5.50.
 ;
Відповідь:
;
Відповідь:
5.51.
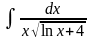 ;
Відповідь:
5.52.
;
Відповідь:
5.52.
 ;
Відповідь:
;
Відповідь:
5.53.
 ;
Відповідь:
5.54.
;
Відповідь:
;
Відповідь:
5.54.
;
Відповідь:
5.55.
 Відповідь:
5.56.
Відповідь:
5.56.
 Відповідь:
Відповідь:
c) Інтегрування частинами
5.59.
 Відповідь:
5.60.
Відповідь:
5.60.
 Відповідь:
Відповідь:
5.61.
 Відповідь:
5.62
Відповідь:
5.62
 Відповідь:
Відповідь:
5.63.
 Відповідь:
5.64.
Відповідь:
5.64.
 Відповідь:
Відповідь:
5.65.
 Відповідь:
5.66.
Відповідь:
5.66.
 Відповідь:
Відповідь:
5.67.
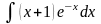 ;
Відповідь:
5.68.
;
Відповідь:
5.68.
 ;
Відповідь:
;
Відповідь:
5.69.
 ;
Відповідь:
5.70.
;
Відповідь:
5.70.
 ;
Відповідь:
;
Відповідь:
5.71.
 ;
Відповідь:
5.72.
;
Відповідь:
5.72.
 ;
Відповідь:
;
Відповідь:
5.73.
 Відповідь:
5.74.
Відповідь:
5.74.
 Відповідь:
Відповідь:
5.75.
 Відповідь:
5.76.
Відповідь:
5.76.
 Відповідь:
Відповідь:
5.77.
 Відповідь:
5.78.
Відповідь:
5.78.
 Відповідь:
Відповідь:
5.79.
 Відповідь:
5.80.
Відповідь:
5.80.
 Відповідь:
Відповідь:
5.81.
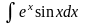 Відповідь:
5.82.
Відповідь:
5.82.
 Відповідь:
Відповідь:
5.83.
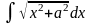 Відповідь:
5.84.
Відповідь:
5.84.
 Відповідь:
Відповідь:
d). Інтегрування раціональних дробів
5.85.
 Відповідь: 5.86.
Відповідь: 5.86. Відповідь:
Відповідь:
5.87.
 Відповідь: 5.88
Відповідь: 5.88
 Відповідь:
Відповідь:
5.89.
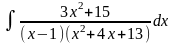 Відповідь: 5.90
Відповідь: 5.90
 Відповідь:
Відповідь:
5.91.
 Відповідь:
5.92.
Відповідь:
5.92.
 Відповідь:
Відповідь:
5.93.
 Відповідь:
5.94.
Відповідь:
5.94.
 Відповідь:
Відповідь:
5.95.
 Відповідь:
5.96.
Відповідь:
5.96.
 Відповідь:
Відповідь:
5.97.
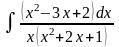 Відповідь:
5.98.
Відповідь:
5.98.
 Відповідь:
Відповідь:
5.99.
 Відповідь:
5.100.
Відповідь:
5.100.
 Відповідь:
Відповідь:
5.101.
 Відповідь:
5.102.
Відповідь:
5.102.
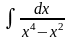 Відповідь:
Відповідь:
5.103.
 Відповідь:
5.104.
Відповідь:
5.104.
 Відповідь:
Відповідь:
e).
Інтегрування раціональних функцій

5.105.
 Відповідь: 5.106.
Відповідь: 5.106.
 Відповідь:
Відповідь:
5.107.
 Відповідь: 5.108.
Відповідь: 5.108.
 Відповідь:
Відповідь:
5.109.
 Відповідь: 5.110.
Відповідь: 5.110.
 Відповідь:
Відповідь:
5.111.
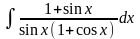 Відповідь: 5.112.
Відповідь: 5.112.
 Відповідь:
Відповідь:
5.113.
 Відповідь:
5.114.
Відповідь:
5.114.
 Відповідь:
Відповідь:
5.115.
 Відповідь:
5.116.
Відповідь:
5.116.
 Відповідь:
Відповідь:
5.117.
 Відповідь:
5.128.
Відповідь:
Відповідь:
5.128.
Відповідь:
5.129.
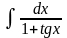 Відповідь:
5.130.
Відповідь:
5.130.
 Відповідь:
Відповідь:
5.131.
 Відповідь:
5.132.
Відповідь:
5.132. Відповідь:
Відповідь:
Інтегрування
ірраціональних функцій:
5.133.
 Відповідь:
5.134.
Відповідь:
5.134.
 Відповідь:
Відповідь:
5.135.
 Відповідь:
5.136.
Відповідь:
5.136.
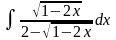 Відповідь:
Відповідь:
5.137.
 Відповідь:
5.138.
Відповідь:
5.138.
 Відповідь:
Відповідь:
5.139.
 Відповідь:
5.140.
Відповідь:
5.140.
 Відповідь:
Відповідь:
5.141.
 Відповідь:
5.142.
Відповідь:
5.142.
 Відповідь:
Відповідь:


