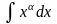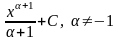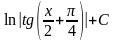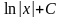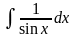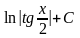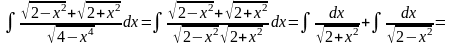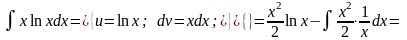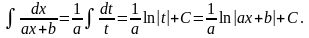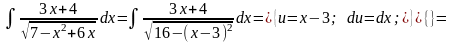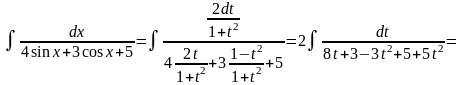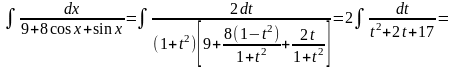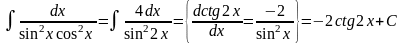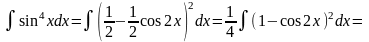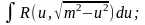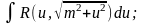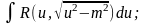- •5. Невизначний інтеграл
- •5.1. Первісна функція і невизначений інтеграл
- •5.2.Основні методи інтегрування
- •1). Тригонометричні підстановки
- •2). Підстановки Ейлера
- •3). Метод невизначених коефіцієнтів.
- •5.3. Задачі для самостійного розв‘язку
- •5.4. Обчислення невизначених інтегралів в середовищі Maxima
5. Невизначний інтеграл
5.1. Первісна функція і невизначений інтеграл
Функція F(x) називається первісною функцією функції f(x) на відрізку [а, b], якщо в будь-якій точці цього відрізку вірна рівність:
Fʹ(x) = f(x).
Невизначеним інтегралом функції f(x) називається сукупність первісних функцій, які визначені співвідношенням
F(x)+ C (С – деяке постійне число).
Позначення невизначеного інтеграла –
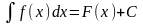 .
(5.1)
.
(5.1)
Властивості невизначеного інтеграла
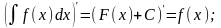
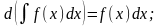
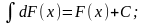
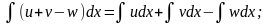 де u, v,
w – деякі функції від х.
де u, v,
w – деякі функції від х.
Таблиця інтегралів
Інтеграл |
Значення |
Інтеграл |
Значення |
|||
1 |
|
-lncosx+C |
9 |
|
ex + C |
|
2 |
|
lnsinx+ C |
10 |
|
sinx + C |
|
3 |
|
|
11 |
|
-cosx + C |
|
4 |
|
|
12 |
|
tgx + C |
|
5 |
|
|
13 |
|
-ctgx + C |
|
6 |
|
ln |
14 |
|
arcsin |
|
7 |
|
|
15 |
|
|
|
8 |
|
|
16 |
|
|
|
5.2.Основні методи інтегрування
Безпосереднє інтегрування. Метод безпосереднього інтегруванням заснований на припущенні про можливе значення первісної функції з подальшою перевіркою цього значення диференціюванням.
Приклад.
1.
Потрібно знайти значення інтеграла
. На основі формули диференціювання
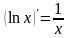 можна зробити вивід, що шуканий інтеграл
дорівнює
можна зробити вивід, що шуканий інтеграл
дорівнює
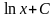 ,
де С
– деяке постійне число. Однак, з іншого
боку
,
де С
– деяке постійне число. Однак, з іншого
боку
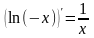 . Таким чином, остаточно можна зробити
вивід:
. Таким чином, остаточно можна зробити
вивід:
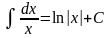 .
.
2.
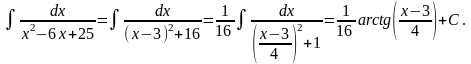
Метод
підстановки (заміна змінної). Якщо
потрібно знайти інтеграл
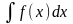 ,
то часто виявляється зручним виробити
заміну змінної інтегрування, вважаючи
x
=
(t)
і dx
= (t)
dt
в результаті отримаємо:
,
то часто виявляється зручним виробити
заміну змінної інтегрування, вважаючи
x
=
(t)
і dx
= (t)
dt
в результаті отримаємо:
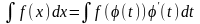 .
.
Приклади. Знайти невизначений інтеграл:
1.
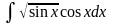 .
.
Зробимо заміну t = sinx, dt = cosx dt.
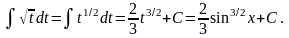
2.
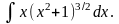
Заміна
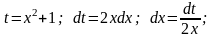 дає:
дає:
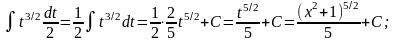
3.
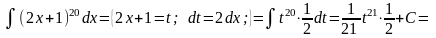
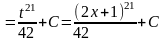
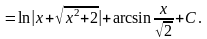
5.
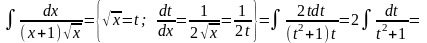
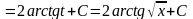
Інтегрування
частинами.
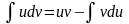 (5.2)
(5.2)
Приклади.
1.
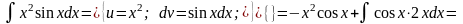
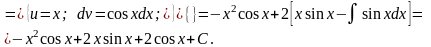
2.
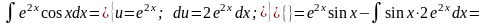
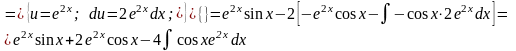
Тоді
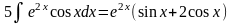 і
і
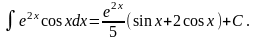
3.
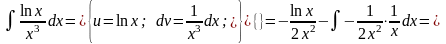
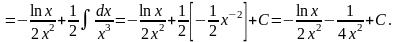
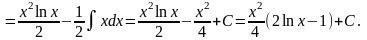
Інтегрування раціональних і дробово-раціональних функцій
1. Інтегрування простих раціональних дробів. До простих раціональних дробів відносяться функції наступних чотирьох типів:
I.
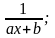 III.
III.
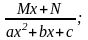
II.
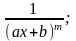 IV.
IV.
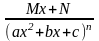
m, n – натуральні числа (m 2, n 2) і b2 – 4ac <0 .
Перші два типи інтегралів від елементарних дробів наводяться до табличних підстановкою t = ах + b.
II.
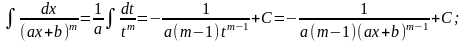
Інтеграл дробу вигляду III може бути представлений у вигляді:
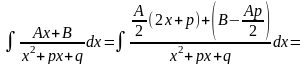
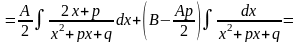
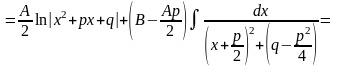
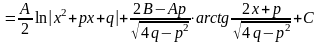
Приклади.
.
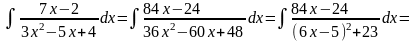 =
=
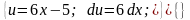
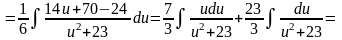
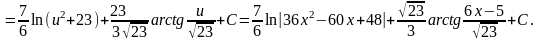
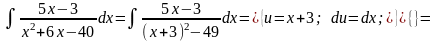
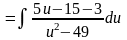 =
=
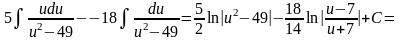
=
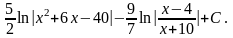
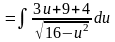
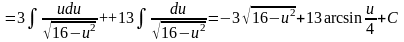 =
=
=
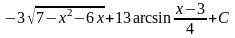 .
.
Розглянемо тепер методи інтеграції простих дробів IV типа.
Спочатку
розглянемо випадок при М
= 0, N
= 1. Тоді інтеграл вигляду
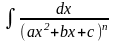 можна шляхом виділення в знаменнику
повного квадрата представити у вигляді
можна шляхом виділення в знаменнику
повного квадрата представити у вигляді
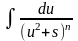 . Зробимо наступне перетворення:
. Зробимо наступне перетворення:
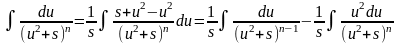 .
.
Другий інтеграл, що входить в цю рівність, братимемо по частинах.
Позначимо:
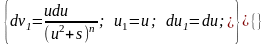
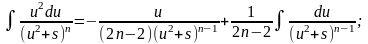
Для вихідного інтеграла отримуємо:
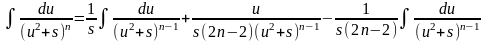
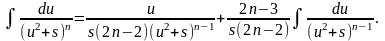
Отримана формула називається рекурентною.
Повернемося тепер до інтеграла від елементарного дробу вигляду IV в загальному випадку.
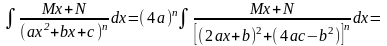
=
 =
=
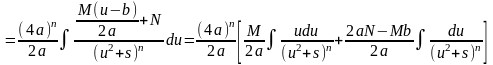
Приклад.
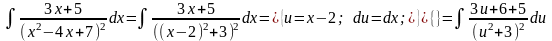 =
=
=
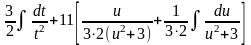 =
=
 =
=
=
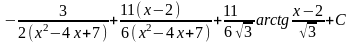 .
.
Інтегрування
дробово-раціональних функцій.
Відношення
двох многочлен-нів
 ( Pm(x)
–
многочлен степені m,
а Qn(x)
– многочлен степені n
) – називається дробово-раціональною
функцією
(раціональним
дробом).
( Pm(x)
–
многочлен степені m,
а Qn(x)
– многочлен степені n
) – називається дробово-раціональною
функцією
(раціональним
дробом).
Всякий неправильний раціональний дріб шляхом ділення чисельника на знаменник можна представить у вигляді суми многочлена і правильного раціонального дробу, тобто
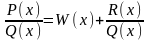 .
.
Якщо
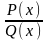 - правильний раціональний дріб, знаменник
Q(x)
якою представлений у вигляді добутку
лінійних і квадратичних множників
- правильний раціональний дріб, знаменник
Q(x)
якою представлений у вигляді добутку
лінійних і квадратичних множників
Q(x)=
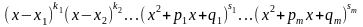 ,
,
то цей дріб може бути представлений у вигляді суми простих дробів:
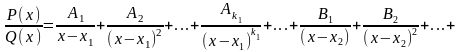
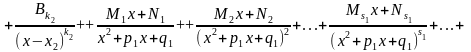
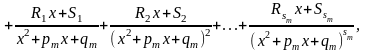
де Ai, A2,…,B1, B2,…,M1, N1,…, R1,S1,… – деякі постійні величини.
Приклади.
1.
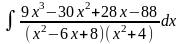
Оскільки
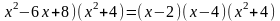 ,
то
,
то
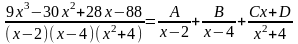
Наводячи до спільного знаменника і прирівнюючи відповідні чисельники, отримуємо:
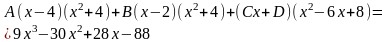
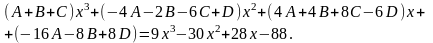
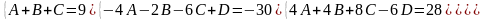
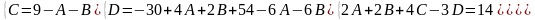
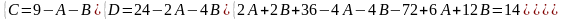
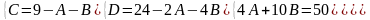
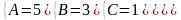
Таким чином
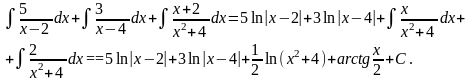
2.
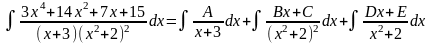
Знайдемо невизначені коефіцієнти:
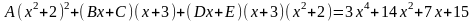
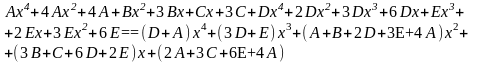

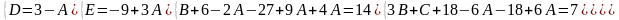
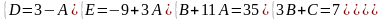
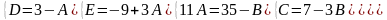
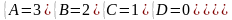
Тоді значення заданого інтеграла:
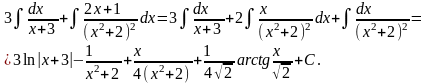
Інтегрування
тригонометричних функцій. Розглянемо
інтеграла вигляду
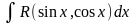 ,
де R
– раціональна функція від змінних sinx
і cosx.
Він обчислюються за допомогою універсальної
підстановки
,
де R
– раціональна функція від змінних sinx
і cosx.
Він обчислюються за допомогою універсальної
підстановки
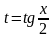 .
Ця підстановка дозволяє перетворити
тригонометричну функцію в раціональну.
.
Ця підстановка дозволяє перетворити
тригонометричну функцію в раціональну.
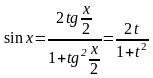 ,
,
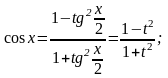
Тоді
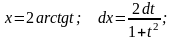
Таким
чином:
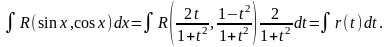
Приклади.

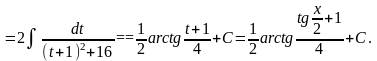
На практиці застосовують і інші, простіші підстановки, залежно від властивостей підінтегральної функції. Інколи зручні наступні правила:
1) якщо функція R є непарною відносно cosx. В цьому випадку зручно скористатися підстановкою sin x = t
Приклад.
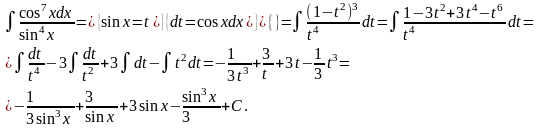
2) якщо функція R є непарною відносно sinx. В цьому випадку застосо-вується підстановка cos x = t
Приклад.
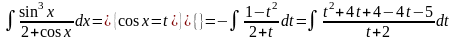 =
=
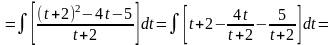
=
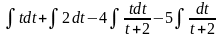 =
=
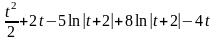 =
=
=
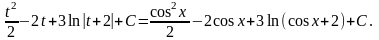
3) якщо функція R парна відносно sinx і cosx. В цьому випадку інтеграл раціоналізується підстановкою tgx = t. Така ж підстановка застосовується, якщо інтеграл має вигляд
Приклад.
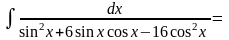
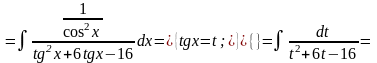
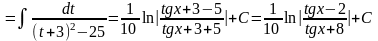 .
.
Інтеграли
типа
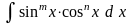
Для знаходження таких інтегралів застосовуються наступні підстановки:
sin x = t, якщо n – ціле позитивне непарне число;
cos x = t, якщо m – ціле позитивне непарне число;
tg x = t, якщо m + n – парне негативне ціле число;
якщо m і n – цілі парні ненегативні числа, то для пониження порядку використовуються формули
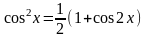
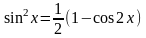 ,
,
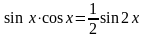 .
.
Приклади.
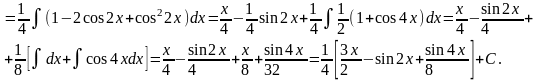
Інтеграли
типа
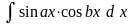 ,
,
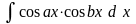 ,
,
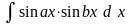
обчислюються за допомогою формул
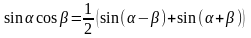 ,
,
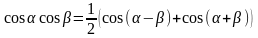 ,
,
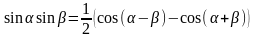 .
.
Приклади.
1.
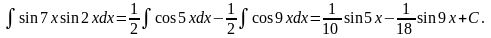
2.
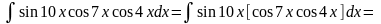
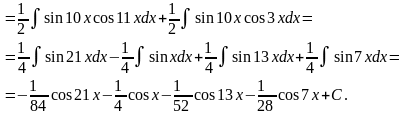
Інтегрування деяких ірраціональних функцій
Інтеграл
вигляду
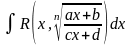 ,
де
n- натуральне число.
,
де
n- натуральне число.
За
допомогою підстановки
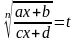 функція раціоналізується
функція раціоналізується
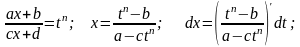
Тоді
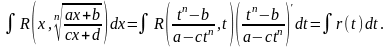
Приклад.
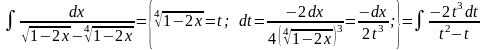 =
=
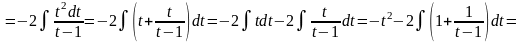

Якщо до складу ірраціональної функції входить коріння різних степенів, то у якості нової змінної треба узяти корінь степені, рівної найменшому загальному кратному степенів коріннів, що входять у вираз.
Приклад.
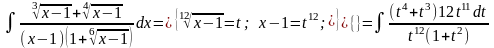 =
=
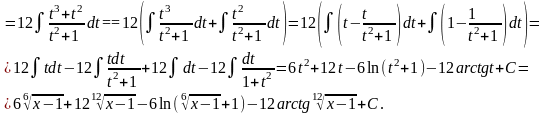
Інтеграли
вигляду
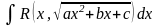 .
Як відомо, квадратний тричлен шляхом
виділення повного квадрата може бути
приведений до вигляду:
.
Як відомо, квадратний тричлен шляхом
виділення повного квадрата може бути
приведений до вигляду:
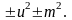
Таким чином, інтеграл наводиться до одного з трьох типів:
Можливі три способи інтегрування таких функцій.

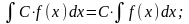
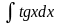
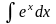
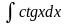
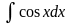
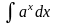
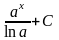
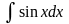

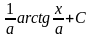
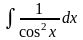
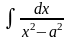
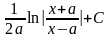
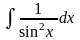
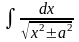
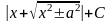

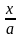 + C
+ C