5.6. Приближённые вычисления с помощью дифференциала
Приближённые вычисления с применением дифференциала функции основаны на приближённой замене приращения функции в точке на её дифференциал
.
(5.11)
Абсолютная погрешность такой замены является, как следует из (5.9), имеет более высокий порядок, чем x.Это равенство позволяет с большой точностью вычислить приближённое приращение любой дифференцируемой функции. Обычно дифференциал находится значительно проще, чем приращение этой функции.
Из равенства (5.11) следует
.
(5.12)
Формула (5.12) используется для вычисления приближённого значения функции.
Примеры. 1) Вычислить приближенно с помощью дифференциала
,
.
Выберем
следовательно
,
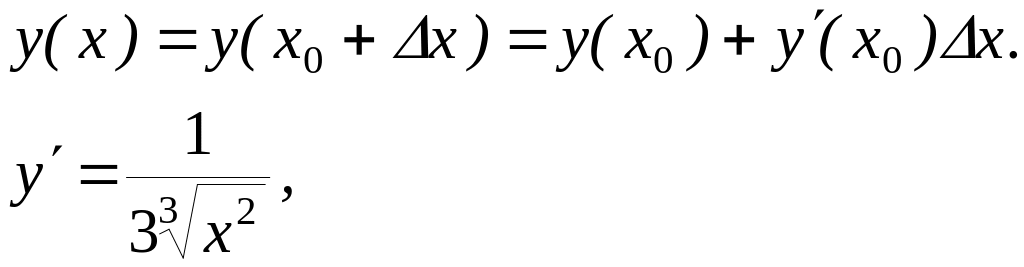
Вычислить приближенно с помощью дифференциала
y = arctg x, x = 0,98.
Выберем
следовательно
Воспользуемся формулой (5.12)
,
,
В
результате arctg
0,98
.
5.7. Исследование функции при помощи производных
Теоремы о среднем
При исследовании поведения дифференцируемых на некотором отрезке [a,b] функций важны следующие теоремы о среднем.
Теорема (Ролль). Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка с, a < с < b, в которой производная f(x) равная нулю, т.е. f(с) = 0.
Доказательство. По свойству функций, непрерывных на отрезке функция f(x) на отрезке [a, b] принимает наибольшее и наименьшее значения. Обозначим эти значения М и m соответственно. Возможны два различных случая М = m и M m.
Пусть M = m. Тогда функция f(x) на отрезке [a, b] сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае в качестве с можно принять любую точку интервала.
Пусть
М
≠ m.
Так как значения на концах отрезка
равны, то функция принимает хотя бы одно
из значений М
или m
во внутренней точке с
интервала (a,b).
Пусть, например, функция принимает
значение М
в точке х
= с (a
< с
< b),
т.е. f(с)
= M.
Так как М
- наибольшее значение функции, то для
всех
выполняется неравенство
.
Найдём производную f(x) в точке х = с:
В
силу предыдущего неравенства выполняется
условие
,
если
,
т.е.
и поэтому
.
Если
же
,
т.е.
,
то
.
Таким
образом,
В случае, когда f(с) = m, доказательство аналогичное.
Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует по крайней мере одна точка с, в которой касательная к графику y = f(x) параллельна оси Ох.
Теорема (Коши). Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g(x) 0 на интервале (a, b), то существует по крайней мере одна точка с, a < с < b, такая, что
.
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке с.
Доказательство. Рассмотрим вспомогательную функцию
,
которая на интервале [a, b] удовлетворяет условиям теоремы Ролля. Легко видеть, что при х = а и х = b F(a) = F(b) = 0. Тогда по теореме Ролля существует такая точка с, a < с < b, такая, что F(с) = 0. Т.к.
,
то
Но
,
то
.
Теорема доказана.
Теорема
(Лагранж). Если
функция f(x)
непрерывна на отрезке [a,
b]
и дифференцируема на интервале (а, b),
то на этом интервале найдется по крайней
мере одна точка с
,
такая, что выполняется равенство
.
(5.13)
Доказательство.
Теорему Лагранжа можно рассматривать,
как частный случай теоремы Коши.
Действительно, положим g(x)
= х, тогда
g(x)=1,
g(с)=1
и
.
Подставляя эти значения в формулу
получаем
или
. Теорема доказана.
Полученное выражение (5.13) называется формулой Лагранжа или формулой конечных приращений. Согласно этой формуле приращение дифференцируемой функции на отрезке [a, b] равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка.
Раскрытие неопределённостей (правила Лопиталя)
К разряду неопределенностей, связанных с вычислением пределов, принято относить следующие соотношения:
.
Теорема (правило Лопиталя) Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.
.
Доказательство. Применив формулу Коши, получим:
где с - точка, находящаяся между а и х. Учитывая, что f(a) = g(a) = 0:
Пусть
при х
а
отношение
стремится к некоторому пределу. Т.к.
точка с
лежит между точками а
и х,
то при х
а
получим с
а, а
следовательно и отношение
стремится к тому же пределу. Таким
образом, можно записать:
. Теорема доказана.
Примеры.
1) Найти предел:
=
=
=
=
0
2)
Найти предел:
.
;
;
;
;
;
;
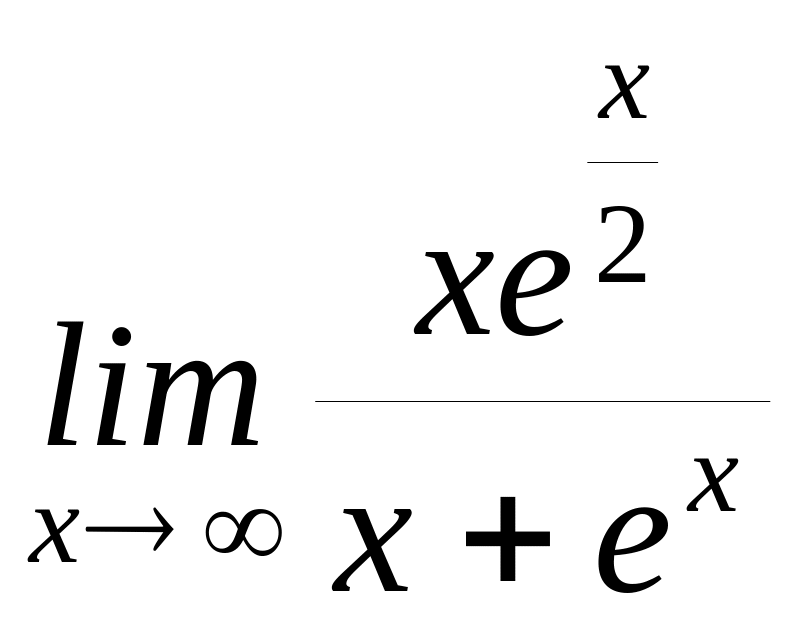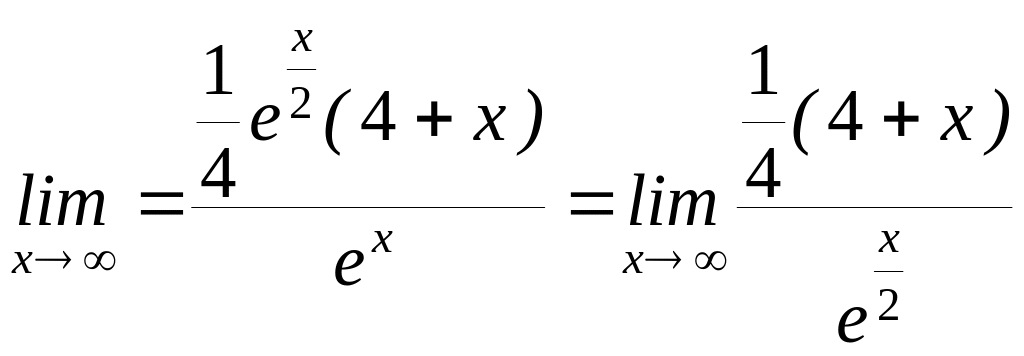
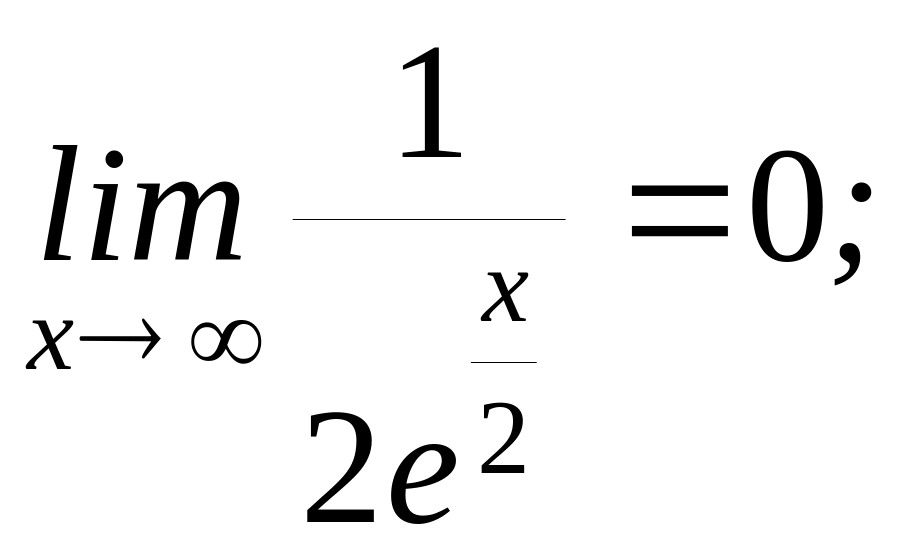
следует заметить, что правило Лопиталя – всего лишь один из способов вычисления пределов. Часто в конкретном примере наряду с правилом Лопиталя может быть использован и какой – либо другой метод (замена переменных, домножение и др.).
3) Найти предел:
.
;
;
- опять получилась
неопределенность.
Применим правило Лопиталя еще раз.
;
;
- применяем правило
Лопиталя еще раз.
;
;
;
Неопределенности
вида
можно раскрыть с помощью логарифмирования.
Такие неопределенности встречаются
при нахождении пределов функций вида
,
f(x)
> 0 вблизи точки а
при х
а. Для
нахождения предела такой функции
достаточно найти предел функции
ln y = g(x) lnf(x).
4).
Найти предел
.
Здесь y = x x, ln y = x lnx.
Тогда
.
Следовательно
5) Найти предел
.
;
-
получили неопределенность.
Применяем правило Лопиталя еще раз.
;
.
Примеры для самостоятельного решения
Найти производную
1)
.
2)
.
3)
4)
.
5)
.
6)
.
Возрастание и убывание функций.
При исследовании функций и построении их графиков важным является выяснение области монотонности (возрастания и убывания) функции.
Теорема 1 (необходимые условия). Если функция f(x) имеет производную на отрезке [a, b] и возрастает (убывает) на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f(x) 0 (f(x) ≤ 0).
Теорема 2 (достаточные условия). Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f(x) > 0 (f(x) < 0) для a < x < b, то эта функция возрастает (убывает) на отрезке [a, b].
Доказательство.
Если функция f(x) возрастает, то f(x + x) > f(x) при x > 0 и
f(x + x) < f(x) при х < 0, тогда:
Пусть f(x) > 0 для любых точек х1 и х2, принадлежащих отрезку [a, b],
причем x1 < x2.
Тогда по теореме Лагранжа: f(x2) – f(x1) = f(с)(x2 – x1), x1 < с < x2
По условию f(с) > 0, следовательно, f(x2) – f(x1) > 0, т.е. функция f(x)
возрастает.
Аналогично можно сделать вывод о том, что если функция f(x) убывает на отрезке [a, b], то f(x) 0 на этом отрезке. Если f(x) < 0 в промежутке (a, b), то f(x) убывает на отрезке [a, b]. Теорема доказана.
Максимум и минимум функций
Определение. Функция f(x) имеет в точке х1 максимум, если ее значение в этой точке больше значений f(x1 + x) < f(x1) во всех точках некоторого интервала, содержащего точку х1. Функция f(x) имеет в точке х2 минимум, если f(x2 +x) > f(x2) при любом х ( х может быть и отрицательным).
Очевидно, что функция, определенная на отрезке может иметь локальный максимум (локальный минимум) только в точках, находящихся внутри этого отрезка. Необходимо различать максимум (минимум) функции и её наибольшее (наименьшее) значение на отрезке – это понятия принципиально различные.
Определение. Точки максимума и минимума функции называются точками экстремума.
Теорема (необходимое условие существования экстремума). Если функция f(x) дифференцируема в точке х = х1 и точка х1 является точкой экстремума, то производная функции обращается в нуль в этой точке.
Доказательство. Предположим, что функция f(x) имеет в точке х = х1 максимум. Тогда при достаточно малых положительных х > 0 верно неравенство:
,
т.е.
Тогда
По определению:
.
Т.е. если х 0, но х < 0, то f(x1) 0, а если х 0, но х > 0, то f(x1) 0.
А это возможно только в том случае, если при х 0 f(x1) = 0.
Для случая, если функция f(x) имеет в точке х2 минимум теорема доказывается аналогично. Теорема доказана.
Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.
Теорема (достаточные условия 1 существования экстремума). Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х1). Тогда если при переходе через точку х1 слева направо производная функции f(x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.
Доказательство.
Пусть
По теореме Лагранжа: f(x) – f(x1) = f(с)(x – x1), где x < с < x1.
Тогда: 1) если х < x1, то с < x1; f(с) > 0; f(с)(x – x1) < 0, следовательно
f(x) – f(x1) < 0 или f(x) < f(x1).
2) если х > x1, то с > x1 f(с) < 0; f(с)(x – x1) < 0, следовательно
f(x) – f(x1) < 0 или f(x) < f(x1).
Таким
образом, значение функции f(x)
в точке х1
является
наибольшим на интервале
,
т.е. f(x)
< f(x1)
в всех точках вблизи х1.
Это означает, что х1
– точка максимума.
Доказательство теоремы для точки минимума производится аналогично.
Теорема (достаточные условия 2 существования экстремума). Если в точке х1 первая производная функции f(x) равна нулю ( f(x1) = 0), а вторая производная в точке х1 существует и отлична от нуля ( f(x1) ≠ 0), то функция f(x) в точке х = х1 имеет максимум, если f(x1) < 0 и минимум, если f(x1) > 0.
Доказательство. Пусть f(x1) = 0 и f(x1) < 0. Т.к. функция f(x) непрерывна, то f(x1) будет отрицательной и в некоторой малой окрестности точки х1.
Т.к. f(x) = (f(x)) < 0, то f(x) убывает на отрезке, содержащем точку х1, но f(x1) = 0, т.е. f(x) > 0 при х < x1 и f(x) < 0 при x > x1. Это и означает, что при переходе через точку х = х1 производная f(x) меняет знак с “+” на “-“, т.е. в этой точке функция f(x) имеет максимум.
Для случая минимума функции теорема доказывается аналогично.
Если f(x) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.
Наибольшее и наименьшее значения функции на отрезке
Пусть функция у = f(x) непрерывна на отрезке [a, b]. Из свойств непрерывных функций следует, что эта функция в указанной области достигает своего наибольшего и наименьшего значений. Причём эти значения функция может принимать либо во внутренней точке отрезка, либо на границе отрезка.
На основе вышесказанного правило нахождения наибольшего и наименьшего значения функции на отрезке сводится к следующим действиям:
Найти критические точки функции.
Найти значения функции в критических точках.
Найти значения функции на концах отрезка.
Выбрать среди полученных значений наибольшее и наименьшее.
Пример. Найти наибольшее и наименьшее значения функции
на
отрезке [-1,3].
Решение. Находим критические точки данной функции, определим производную функции
;
откуда f(x) = 0 при х1 = 1 и при х2 = 2 , обе эти точки принадлежат отрезку [-1,3] . Находим значения функции в критических точках х1 , х2 и на концах отрезка -1 , 3: f(1) = 1, f(2) = 0, f(-1) = -27, f(3) = 5. Сравнивая данные величины, находим наибольшее и наименьшее значения
fниб = 5 в точке х = 3, fним = -27 в точке х = -1.
Задачи для самостоятельного решения
Найти наименьшее и наибольшее значения функции
1)
[-2;1]
. 2)
[2;4] .
3)
[-2;-0,5]
. 4)
[-2;1]
.
Выпуклость (вогнутость) графика функции. Точки перегиба.
Определение. Кривая обращена выпуклостью вверх на некотором интервале, если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой (см. рис 5.3).
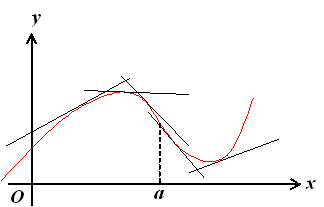
Рис. 5.3. Иллюстрация определения выпуклости и вогнутости
графика функции (при x < a кривая выпукла, при x > a кривая вогнута,
при x = a - точка перегиба) .
Теорема.
Если во всех
точках интервала (a,
b)
вторая производная функции f(x)
(
)
отрицательна, то кривая y
= f(x)
выпукла. Если же
в любой точке
интервала
(a,
b),
то кривая y
= f(x)
вогнута.
Доказательство. Пусть х0 (a, b). Проведем касательную к кривой в этой точке.
Уравнение
кривой: y
= f(x);
уравнение касательной:
Следует доказать,
что
.
По теореме Лагранжа для f(x) – f(x0):
,
x0
< c
< x.
По теореме Лагранжа
для
Пусть
х > x0
тогда x0
< c1
< c
< x.
Т.к. x
– x0
> 0 и c
– x0
> 0, и кроме
того по условию
,
следовательно,
.
Пусть
x
< x0
тогда x
< c
< c1
< x0
и x
– x0
< 0, c
– x0
< 0, т.к. по
условию
то
.
Аналогично доказывается, что если f(x) > 0 на интервале (a, b), то кривая y = f(x) вогнута на интервале (a, b). Теорема доказана.
Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная пересекает кривую.
Теорема (достаточное условие точек перегиба). Пусть кривая определяется уравнением y = f(x). Если вторая производная f(a) = 0 или f(a) не существует и при переходе через точку х = а f(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
Доказательство. 1) Пусть f(x) < 0 при х < a и f(x) > 0 при x > a. Тогда при x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба (см рис. 5.3).
2) Пусть f(x) > 0 при x < b и f(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба. Теорема доказана.
Пример. Определить точки перегиба функции y = x3 + 2x2 + x. Находим производные
;
;
→
.
Определим
поведение функции
при
и при
. Результаты исследования представим
в таблице
-
x
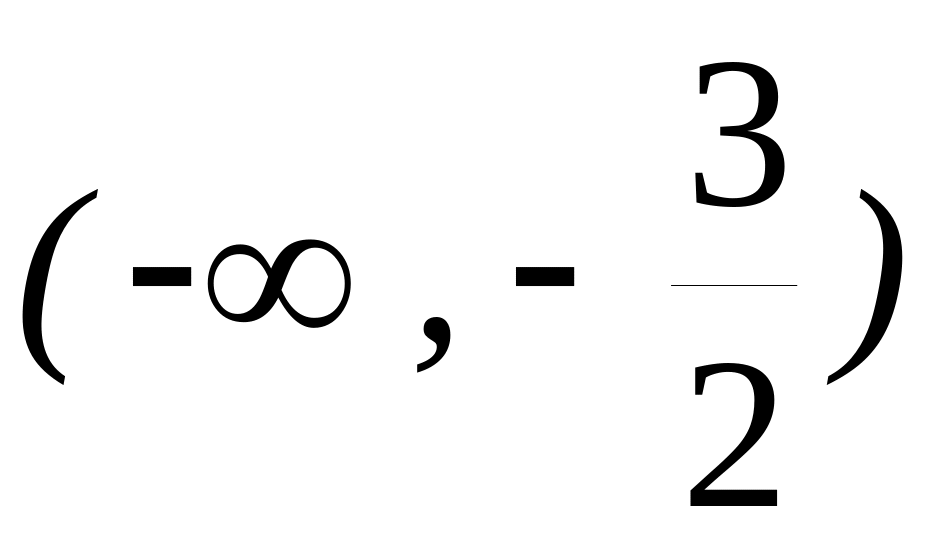
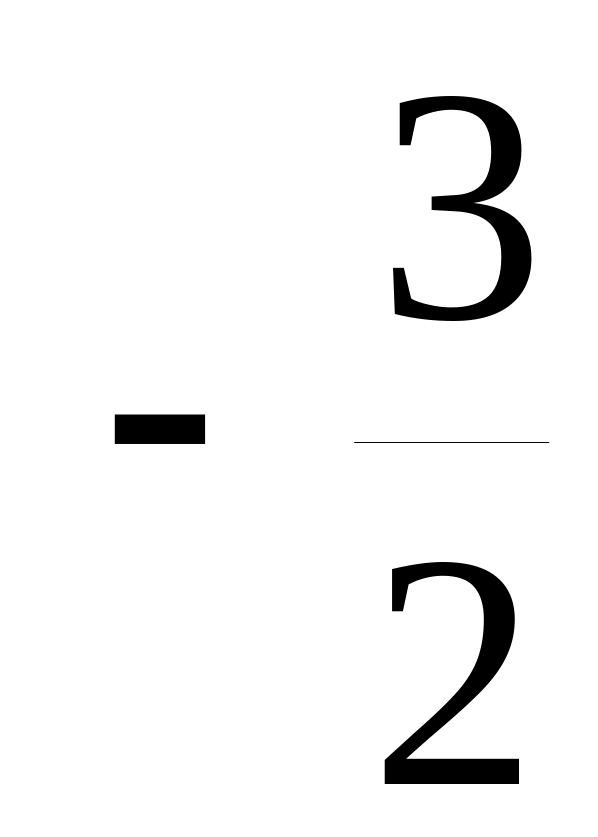
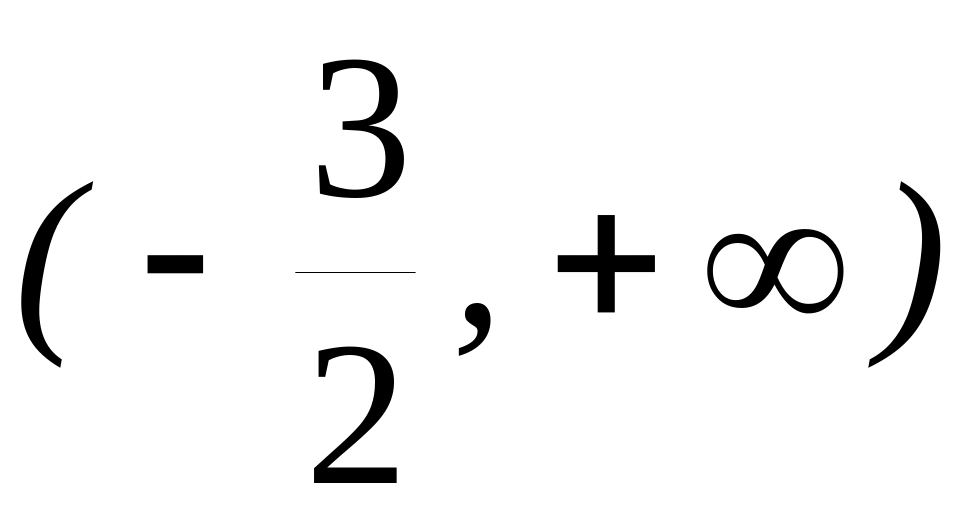
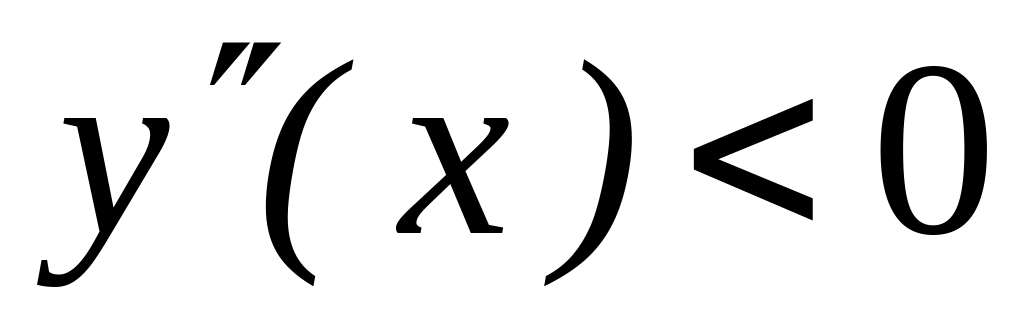
0
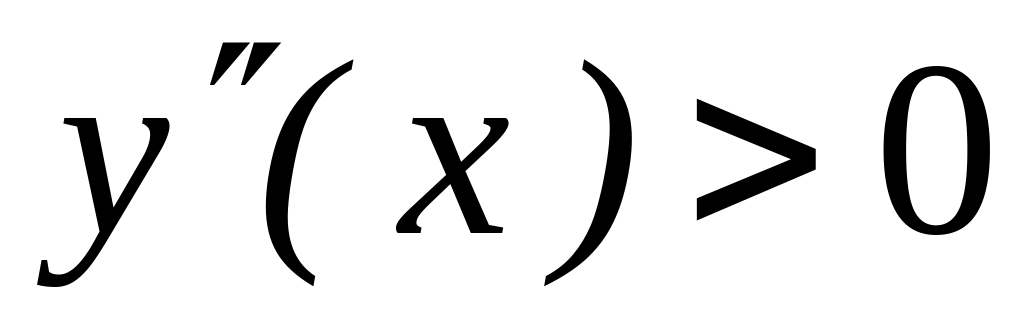
выпукла
точка перегиба
вогнута
Асимптоты графика функции
Часто оказывается, что график функции при удалении текущей точки кривой на бесконечность неограниченно приближается к некоторой прямой. Такие прямые называются асимптотами. Исследование функций на наличие асимптот имеет большое значение при определении характера поведение графика кривой. Следует отметить, что не любая кривая имеет асимптоты. При наличии у кривой асимптот различают три их вида: вертикальные, горизонтальные и наклонные.
Определение.
Прямая х
= а называется
вертикальной
асимптотой
графика функции y
= f(x),
если
или
или
.
Например,
для функции
прямая х
= 5 является вертикальной асимптотой,
так как
,
.
Определение.
Прямая
называется наклонной
асимптотой
графика функции y
= f(x)
при
,
если f(x)
можно представить в виде
f(x)
=
,
где
при
.
Это определение относится также и к горизонтальной асимптоте, если k = 0.
Для
точного определения наклонной асимптоты
необходимо найти способ вычисления
коэффициентов k
и b.
Разделим обе части предыдущего равенства
на х
и переходя к пределу когда
,
получим
, т.е.
.
(5.14)
Затем
из равенства
,
переходя к пределу при
,
получим
,
т.е.
.
(5.15)
Пример.
Найти асимптоты функции
.
Прямая х = -2 является вертикальной асимптотой кривой.
Найдем наклонные асимптоты.
.
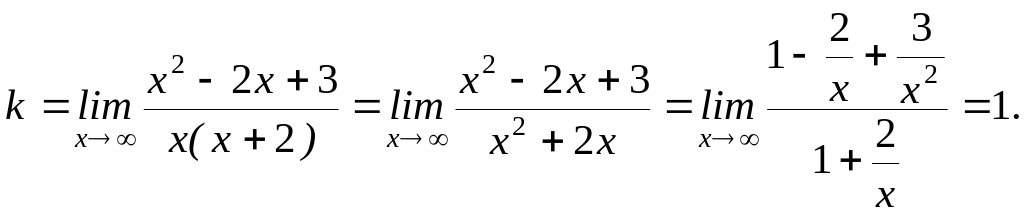
Таким образом, прямая у = х – 4 является наклонной асимптотой.
Схема исследования графика функции
Приведенный в разделе 5.6 теоретический обзор свойств функций позволяет рекомендовать следующую схему проведения исследования функций и построения их графиков.
Найти область определения функции у = f(x).
Определить возможный тип симметрии функции: четность или нечетность функции.
При наличии симметрии достаточно построить график функции на правой координатной полуплоскости и затем отобразить его на левую половину: зеркально относительно оси Оу в случае четности f(x) или с центральной симметрией при нечетности f(x).
3. Найти точки пересечения графика функции с осями координат Ох и Оу,
т. е. решить соответственно уравнения у = f(0) и f(x) = 0.
4. Найти асимптоты.
5. Найти точки возможного экстремума.
6. Найти критические точки.
7. Исследовать знаки первой и второй производных, определить участки монотонности функции, направление выпуклости графика, точки экстремума и перегиба.
8. Определить максимум и минимум функции на области ее определения. Если областью определения функции является отрезок [а, Ь], необходимо вычислить значения функции в его концах и сопоставить их с локальными экстремумами.
9. Построить график функции с учетом проведенного исследования.
Пример.
Исследовать функцию
и построить ее график.
1. Областью определения функции являются все значения х, кроме х = 0.
2. Функция является функцией общего вида в смысле четности и нечетности.
3. Точки пересечения с координатными осями:
c
осью Ох:
y
= 0; x
=
; с осью Оу:
x
= 0; y
– не существует.
4.
Точка х
= 0 является точкой разрыва
,
следовательно, прямая х
= 0 является вертикальной асимптотой.
Наклонные асимптоты ищем в виде: y = kx + b.
Наклонная асимптота у = х.
5. Находим точки экстремума функции.
;
y
= 0 при х
= 2, у
=
при х
= 0.
y > 0 при х (-, 0) – функция возрастает,
y < 0 при х (0, 2) – функция убывает,
у > 0 при х (2, ) – функция возрастает.
Таким образом, точка (2, 3) является точкой минимума.
Для определения характера выпуклости/вогнутости функции находим вторую производную.
> 0 при любом х
0, следовательно, функция вогнутая на
всей области определения.
6. Построим график функции.
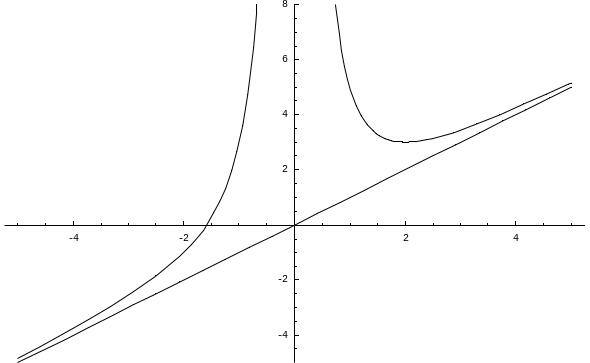
Рис. 5.4. График функции .