5.3. Производные высших порядков

Пусть мы нашли от функции у = f(х) ее производную у′ = f ′(х). Производная от этой производной и называется производной второго порядка от функции f(х) и обозначается y′′ или f ′′(х) или . Аналогично определяются и обозначаются: производная третьего порядка у′′′ = f′′′(x) = ;

производная четвертого порядка у^IV= f^IV(x) = ;….

производная n-oго порядка у⁽ⁿ⁾ = f ⁽ⁿ⁾(x) = .

Примеры. 1) у = 5х⁴ – 3х³ + 2х – 2. Найти у′′.

Решение. Находим в начале первую производную: у′ = 20х³ – 9х² +2, потом вторую от первой производной: у′′ = 60х² – 18х.

2) y = х sinx. Найти у′′′.

Решение. y` = sin x + x cos x

y′′ = cosx + cosx – x sinx = 2cosx – x sinx

y′′′ = -2sinx – sinx – x cosx = -3sinx – x cosx.

5.4. Дифференциал функции

Пусть функция y = f(x) имеет производную в точке х:

Тогда можно записать: , где   0, при х  0.

Следовательно: . (5.9)

Величина x - бесконечно малая более высокого порядка, чем f(x)x, т.е. f(x)x- главная часть приращения у.

Определение. Дифференциалом функции f(x) в точке х называется главная линейная часть приращения функции.

Дифференциал функции обозначается как dy или df(x).

Из определения дифференциала следует, что dy = f(x)x или

dy = f(x)dx. (5.10)

Геометрический смысл дифференциала

Выясним геометрический смысл дифференциала. Для этого проведём к графику функции у = f(x) в точке М(х,у) касательную МК и определим ординату этой касательной для точки (см. рис. 5.2). На рисунке |LM| = Δx, |LN| = Δy.

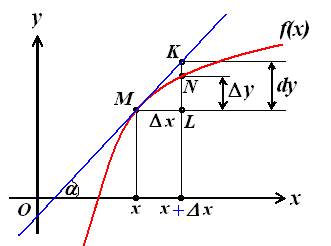
Рис. 5.2.

Из прямоугольного треугольника MKL (рис 5.2) : KL = dy = tgx = yx, т.е. дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.

Свойства дифференциала.

Если u = f(x) и v = g(x )- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:

1. d(u  v) = (u  v)dx = udx  vdx = du  dv,

2. d(uv) = (uv)dx = (uv + vu)dx = vdu + udv,

3. d(Cu) = Cdu,

4. .

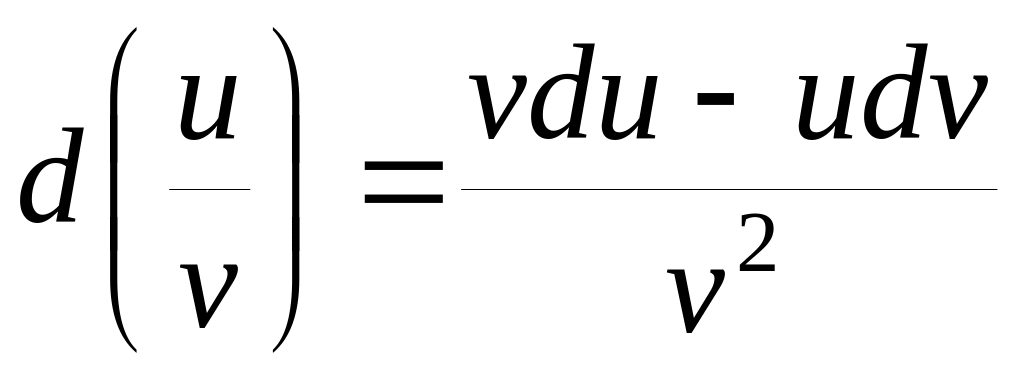5.5. Дифференцирование с помощью пакета Maxima

Пакет Maxima предоставляет мощные средства для дифференцирования функций и вычисления дифференциалов. Для вычисления простейшей производной следует в командном окне после приглашения Maxima ввести команду следующего вида:

diff(<функция>,<переменная>);

где <функция> – выражение, задающее функцию (не обязательно одной переменной), напрмер 4*х^5+3*x^2-5 ;

<переменная> – имя переменной, по которой будет вестись дифференцирование, например x;

С помощью команды diff можно вычислять производные высших порядков. При этом команда эта команда имеет следующий формат:

diff(<функция>,<переменная>,<порядок>);

где <порядок> - порядок вычисляемой производной.

Примеры. 1) Найти производную второго порядка функции

(%i5) d2:diff((x)^cos(x),x,2);

(%o5) x^cos(x)*(cos(x)/x-log(x)*sin(x))^2+x^cos(x)*(-(2*sin(x))/x-cos(x)*log(x)-cos(x)/x^2)

2) Найти производную третьего порядка функции

(%i6) d3:diff(cos(8*x^2),x,3);

(%o6) 4096*x^3*sin(8*x^2)-768*x*cos(8*x^2).

3) Найти дифференциал функции двух переменных

(%i8) diff(2*x*y+y/(3*x));

(%o8) (2*x+1/(3*x))*del(y)+(2*y-y/(3*x^2))*del(x)