- •5. Дифференциальное исчисление функции одной переменной.
- •5.1. Производная функции, ее геометрический и физический смысл.
- •5.2. Основные правила дифференцирования функций
- •5.3. Производные высших порядков
- •5.4. Дифференциал функции
- •5.5. Дифференцирование с помощью пакета Maxima
- •5.6. Приближённые вычисления с помощью дифференциала
- •5.7. Исследование функции при помощи производных
- •5.8. Определение максимума и минимума функции с помощью пакета Maxma
5. Дифференциальное исчисление функции одной переменной.
5.1. Производная функции, ее геометрический и физический смысл.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
![]() .
(5.1)
.
(5.1)
 у
у
f(x)
f(x0 +x) P
f
f(x0) M
x
0 x0 x0 + x x
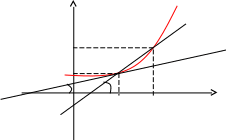
Рис. 5.1.
Пусть
f(x)
определена на некотором промежутке (a,
b).
Тогда
![]() тангенс угла наклона секущей МР к графику
функции.
тангенс угла наклона секущей МР к графику
функции.
![]() ,
,
где - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение
касательной к кривой:
![]() (5.2)
(5.2)
Уравнение
нормали к кривой:
![]() .
(5.3)
.
(5.3)
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t - время, а f(t)- закон движения – мгновенная скорость движения.
Соответственно, вторая производная функции - скорость изменения скорости, т.е. ускорение.
Функция у= f(x), имеющая производную в каждой точке интервала (а, b), называется дифференцируемой в этом интервале. Соответственно операция нахождения производной функции называется дифференцированием.
Рассмотрим основные свойства дифференцируемых функций.
Теорема 1 (необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точке.
Теорема 2. Если функция у = f(x) на интервале (а, b) монотонна и имеет в произвольной точке х этого интервала производную
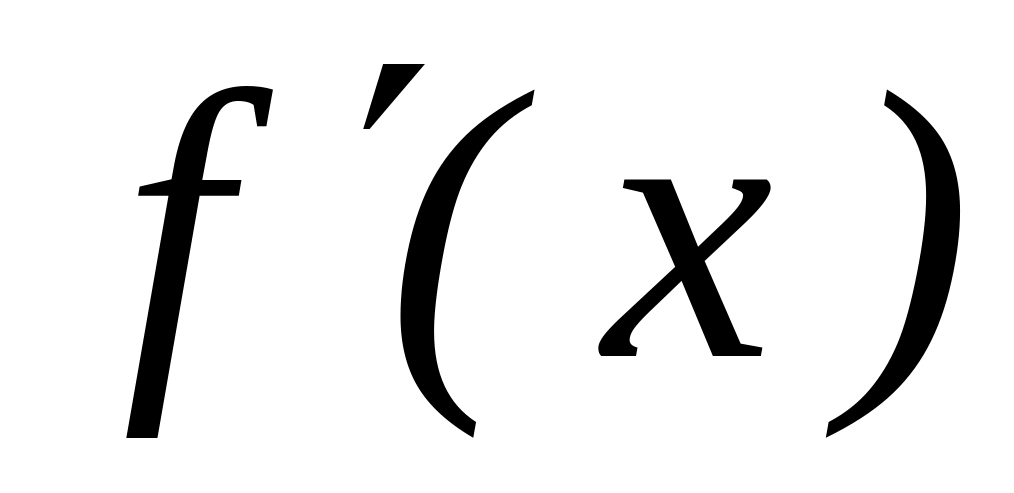 не
равную нулю, то обратная ей функция х
= φ (у) также
имеет производную
не
равную нулю, то обратная ей функция х
= φ (у) также
имеет производную
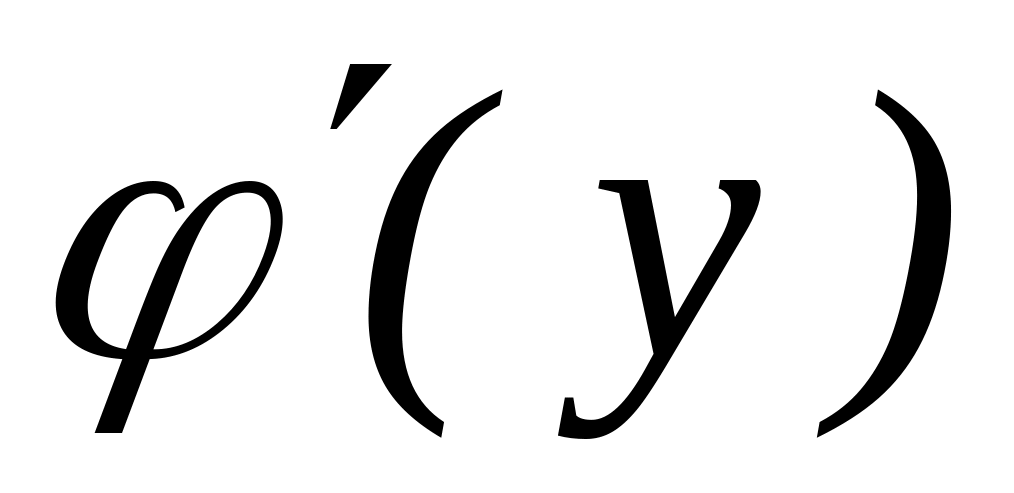 в соответствующей точке и равна
в соответствующей точке и равна
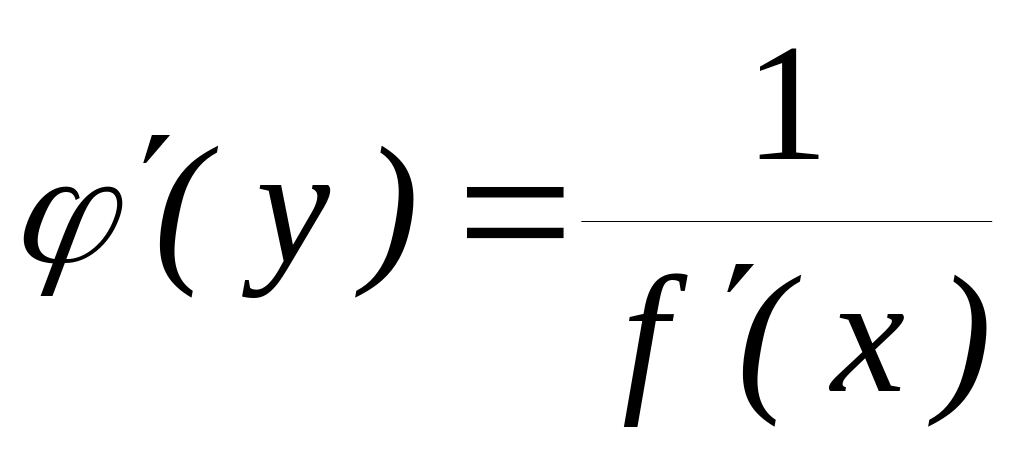 .
(5.4)
.
(5.4)
Следовательно, производная обратной функции равна обратной величине производной данной функции.
5.2. Основные правила дифференцирования функций
На практике нахождение производной функции часто связано с определёнными трудностями, поэтому удобно пользоваться в дальнейшем следующими правилами дифференцирования.
Пусть функции u = u (x) и v = v(x) – дифференцируемы в точке х . а C – постоянная величина (C = const). Имеют место следующие правила:
1)
![]() ;
;
2)
![]() ;
;
(u v) = u v ;
(uv) = uv + uv ;
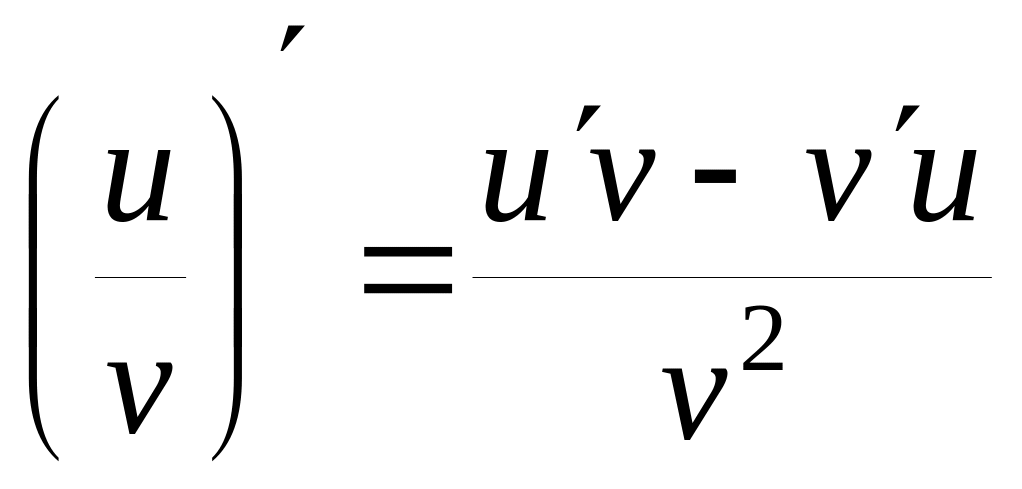 ,
если v
0 .
,
если v
0 .
Эти правила могут быть легко доказаны на основе теорем о пределах.
Ниже приводится таблица производных элементарных функций:
-
1) С = 0
9)
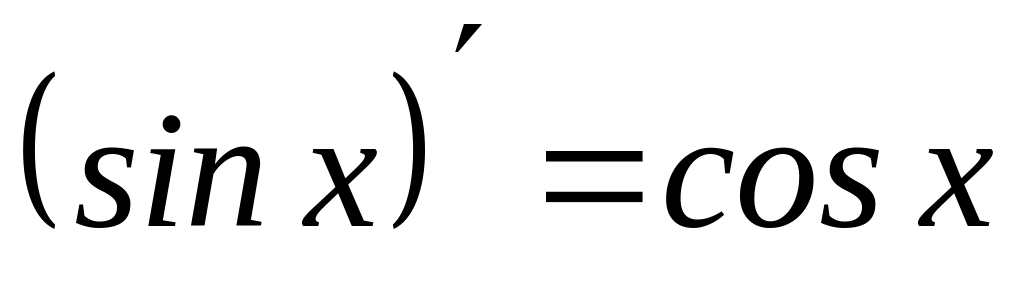
2) ( xm ) = m xm-1
10)
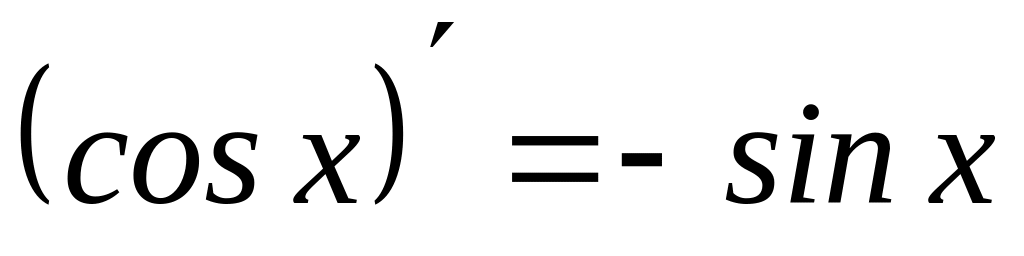
3)
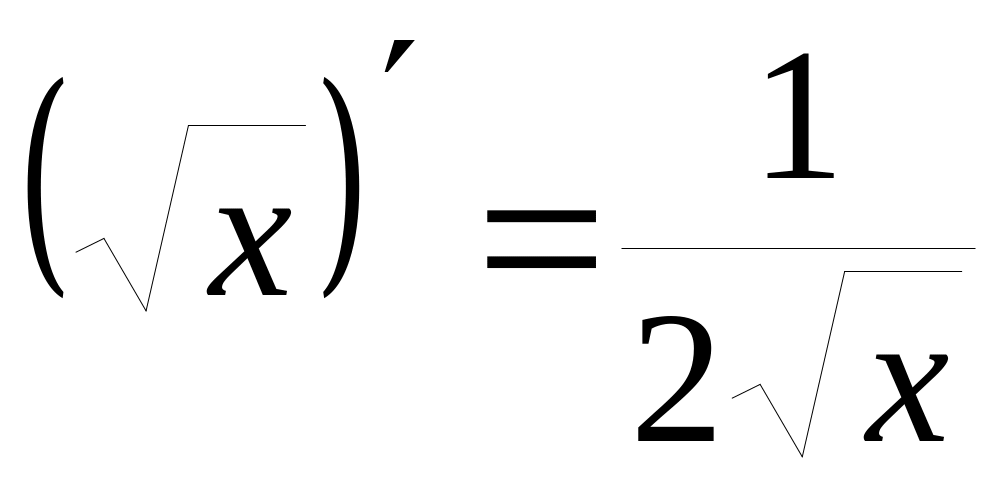
11)
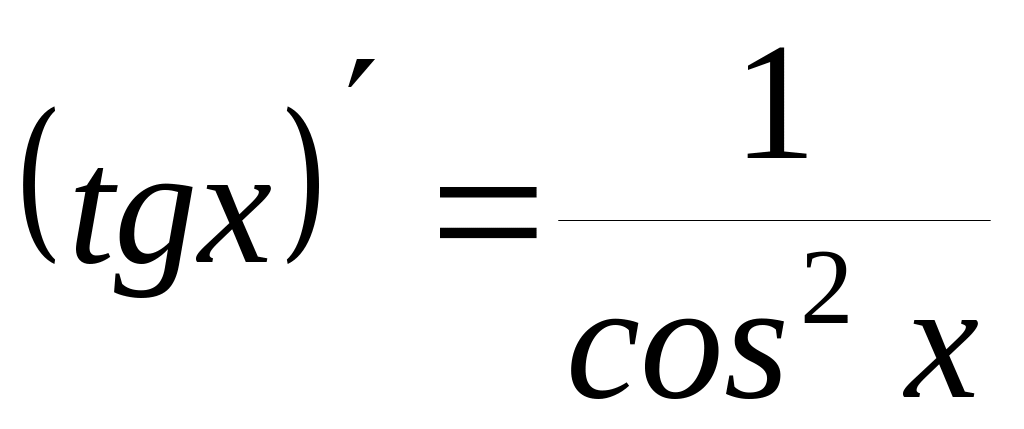
4)
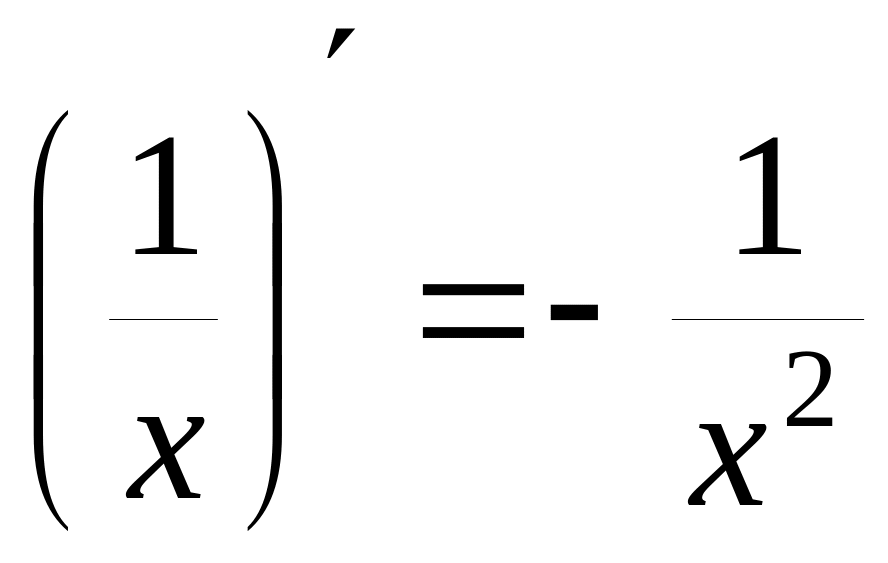
12)
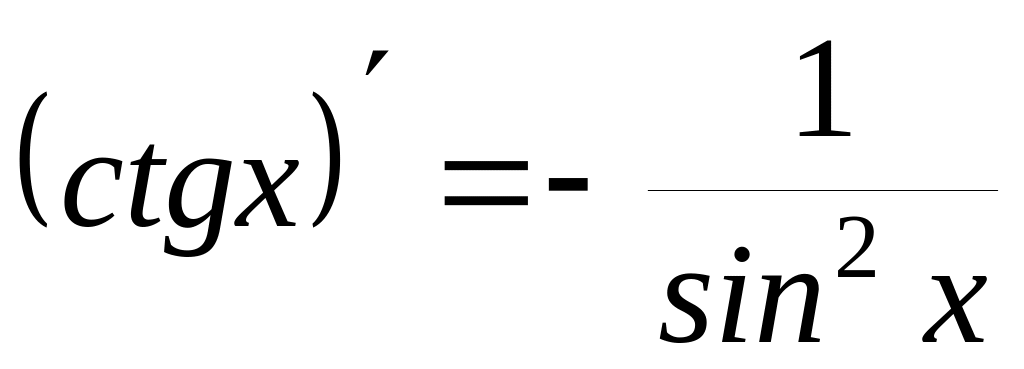
5)

13)
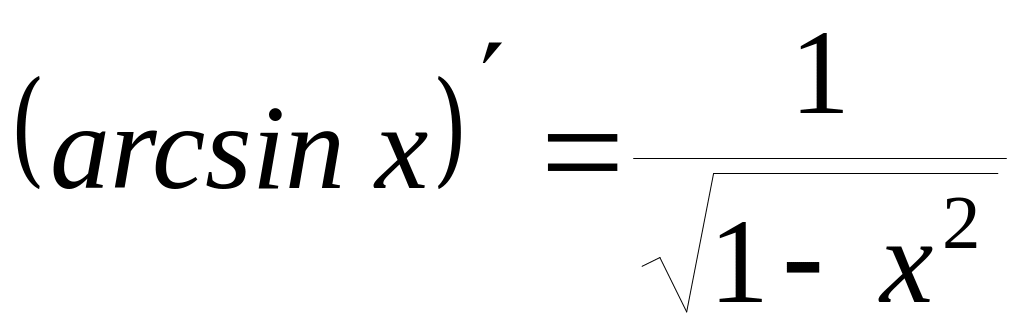
6)
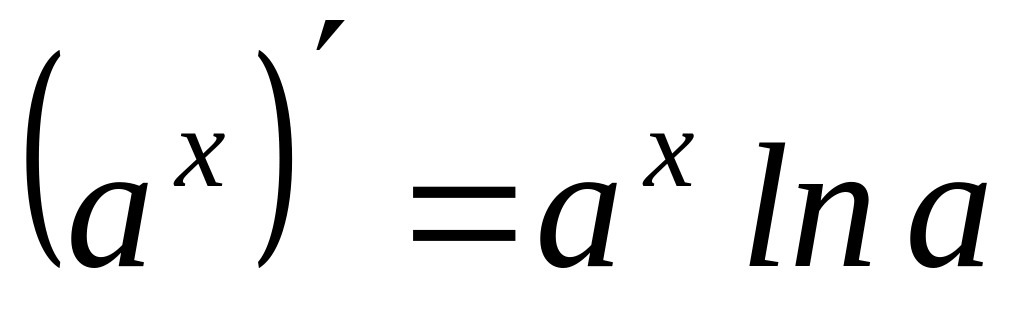
14)
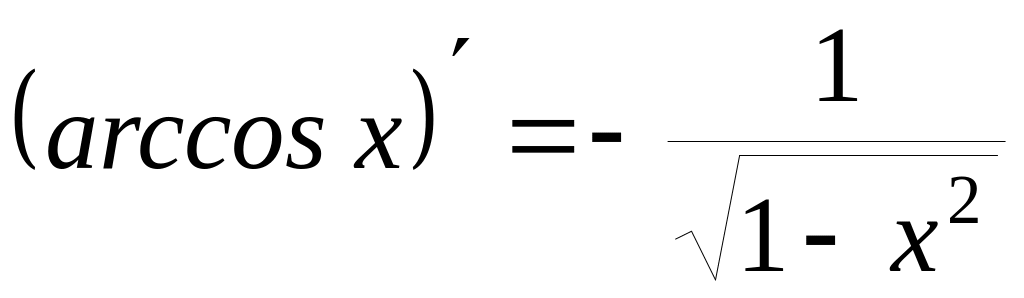
7)
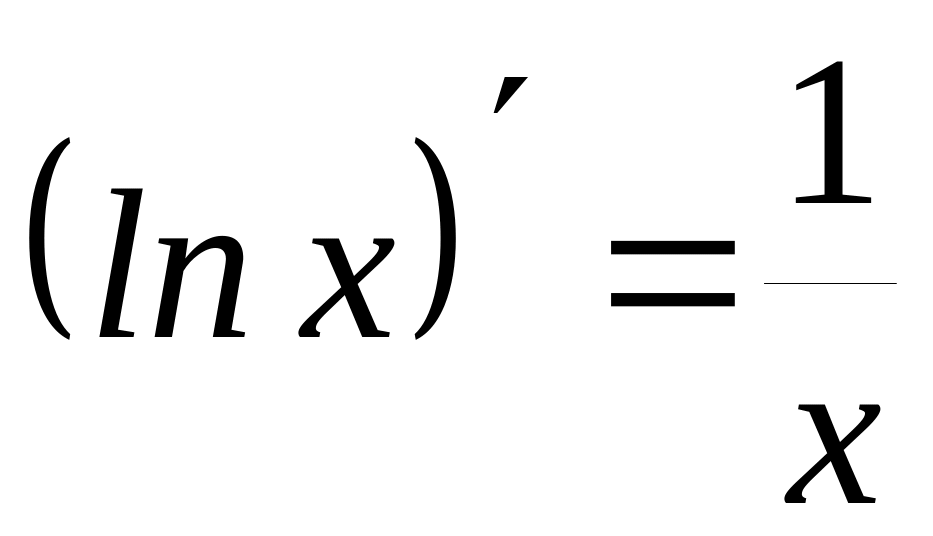
15)
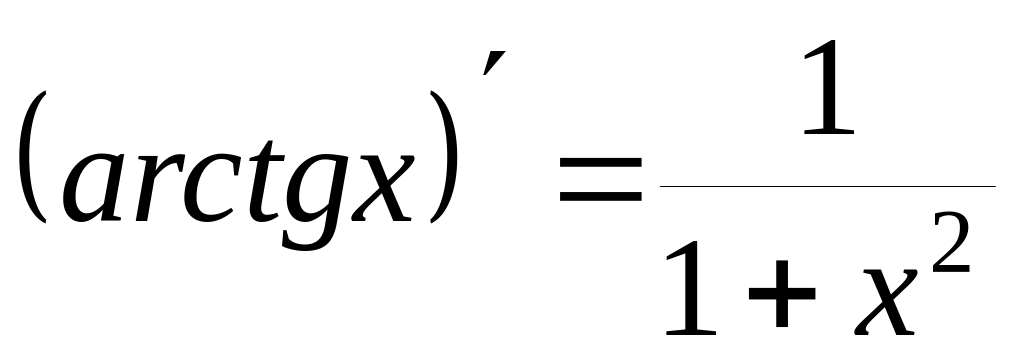
8)
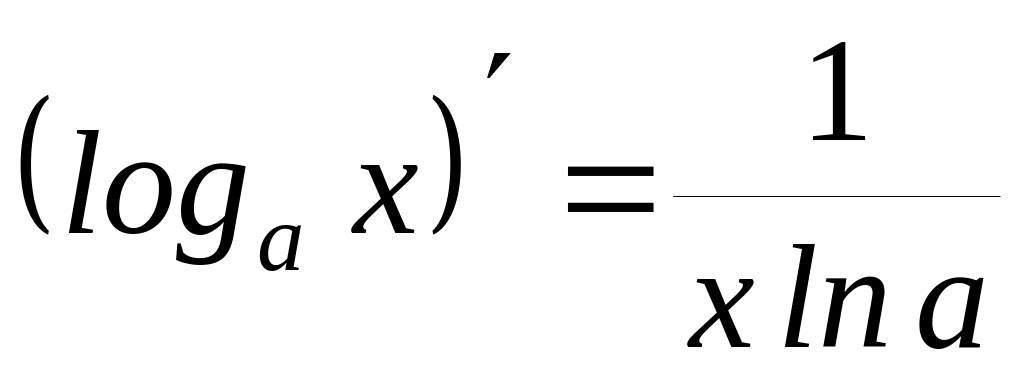
16)
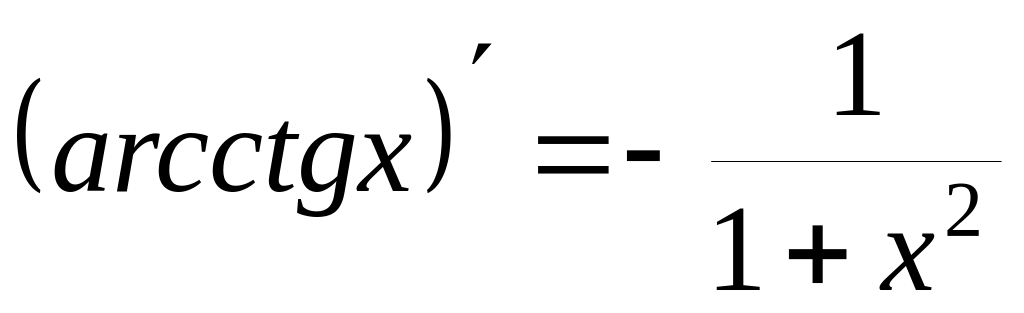
Производная сложной функции.
Теорема. Пусть функции y = f(u) и u = g(x) дифференцируемы в соответствующей точке, причем область значений функции g(x) входит в область определения функции f.
Тогда
![]() .
(5.5)
.
(5.5)
Доказательство.
![]() ,
,
![]()
( с учетом того, что если x0, то u0, т.к. u = g(x) – непрерывная функция)
Тогда
![]() Теорема доказана.
Теорема доказана.
Примеры. Найти производную
1)
![]()
![]()
2)
![]()
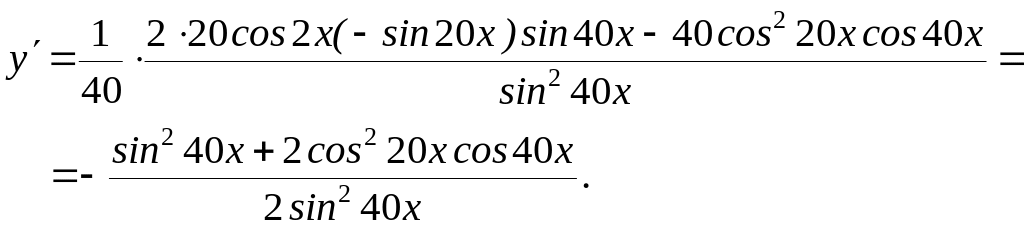
Логарифмическое дифференцирование.
На практике в ряде случаев для нахождения производной функции удобно вначале прологарифмировать эту функция, а затем результат продифференцировать. Такая двойная процедура называется логарифмическим дифференцированием. Метод логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.
Рассмотрим
функцию
![]() .
.
Тогда
(lnx)=
![]() ,
т.к.
,
т.к.
![]() .
Учитывая полученный результат, можно
записать
.
Учитывая полученный результат, можно
записать
![]() .
Здесь отношение
.
Здесь отношение
![]() называется логарифмической
производной
функции f(x).
называется логарифмической
производной
функции f(x).
В
результате
![]() . (5.6)
. (5.6)
Примеры. 1) Производная степенно-показательной функции
![]() .
(5.7)
.
(5.7)
2)
![]() ,
,
![]()
3)
![]() ,
,
![]() .
.
Функция, заданная параметрически
Пусть зависимость между аргументом х и функцией у задана в параметрическом виде
![]() ,
где t
– параметрическая переменная.
,
где t
– параметрическая переменная.
Найдём
производную
![]() ,
считая, что функции x(t)
и y(t)
имеют производные и кроме того x(t)
имеет обратную функцию t
= φ(х).
По правилу дифференцирования обратной
функции (5.4)
,
считая, что функции x(t)
и y(t)
имеют производные и кроме того x(t)
имеет обратную функцию t
= φ(х).
По правилу дифференцирования обратной
функции (5.4)
![]() .
.
По
правилу дифференцирования сложной
функции (5.5) имеем:
![]() , в результате
, в результате
![]() ,
т.е.
,
т.е.
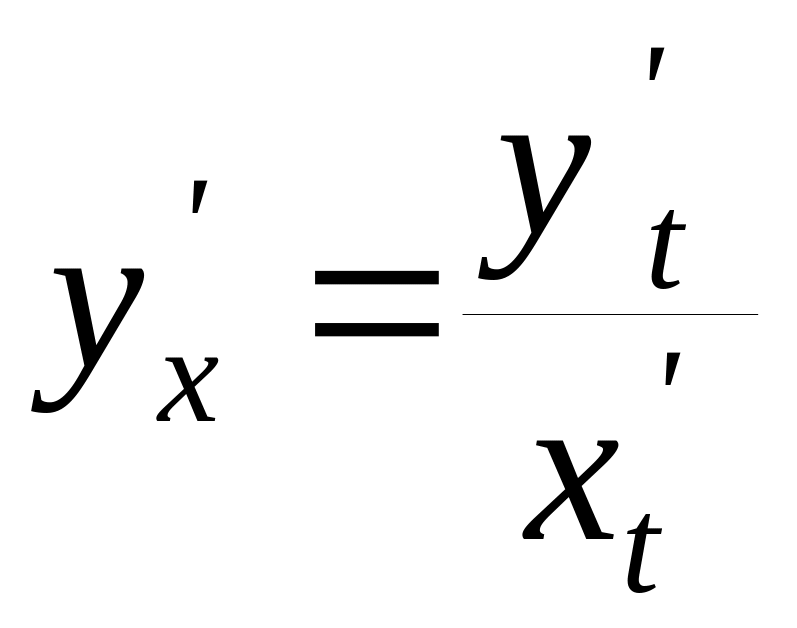 . (5.8)
. (5.8)
Полученная
формула (5.8) позволяет находить производную
![]() если зависимость у
от х
задана параметрически.
если зависимость у
от х
задана параметрически.
Пример.
![]()
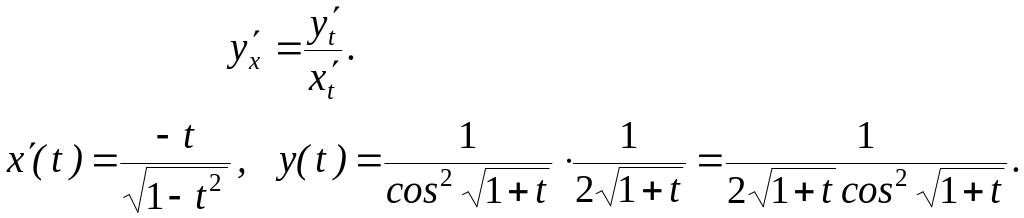
![]()
Примеры для самостоятельного решения
Найти производную
1)
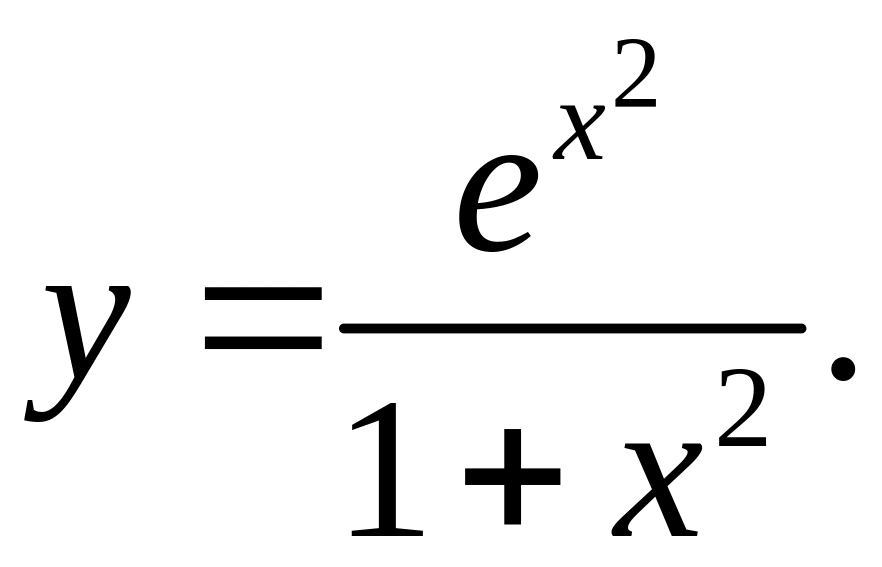 2)
2)
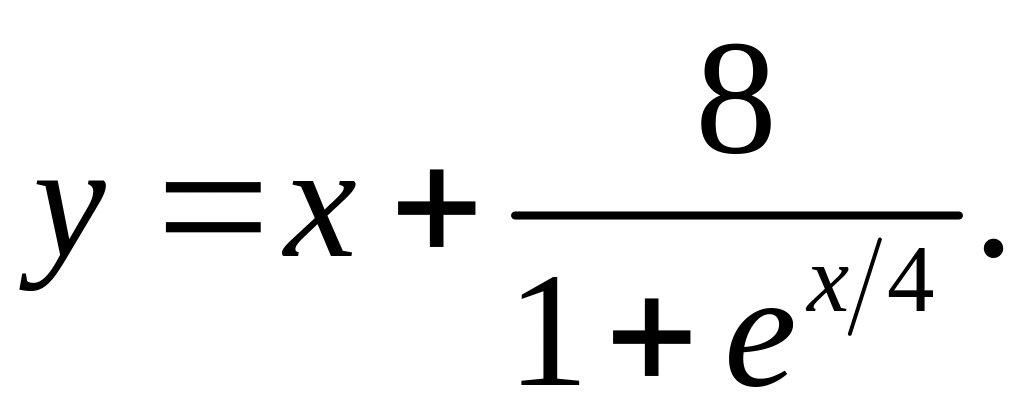 3)
3)
![]() 4)
4)
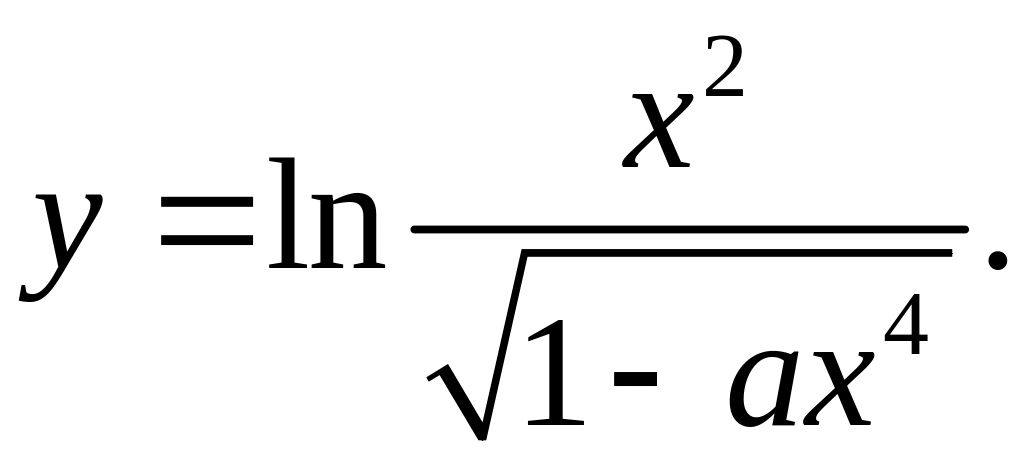
5)
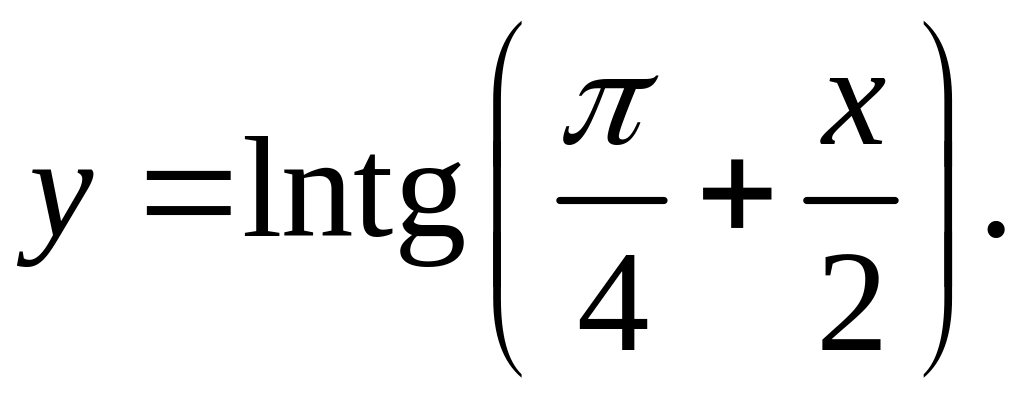 6)
6)
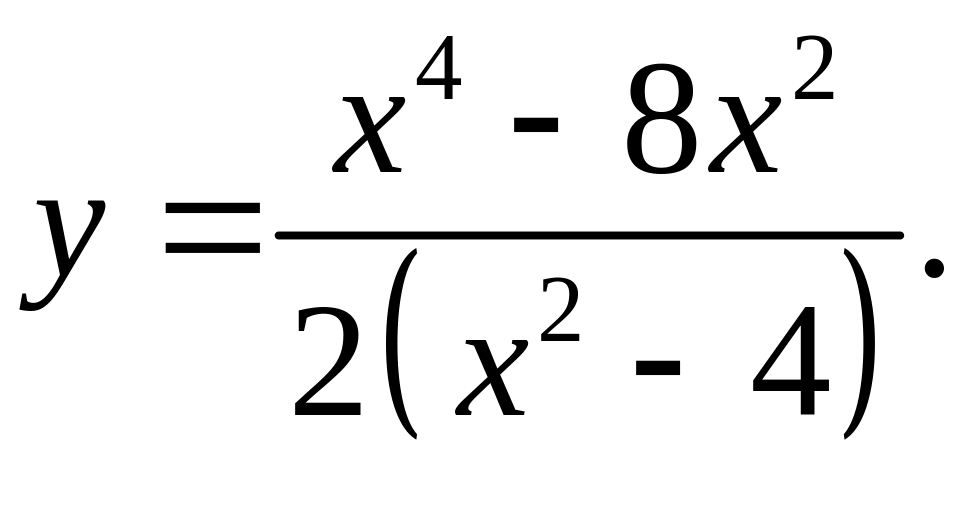 7)
7)
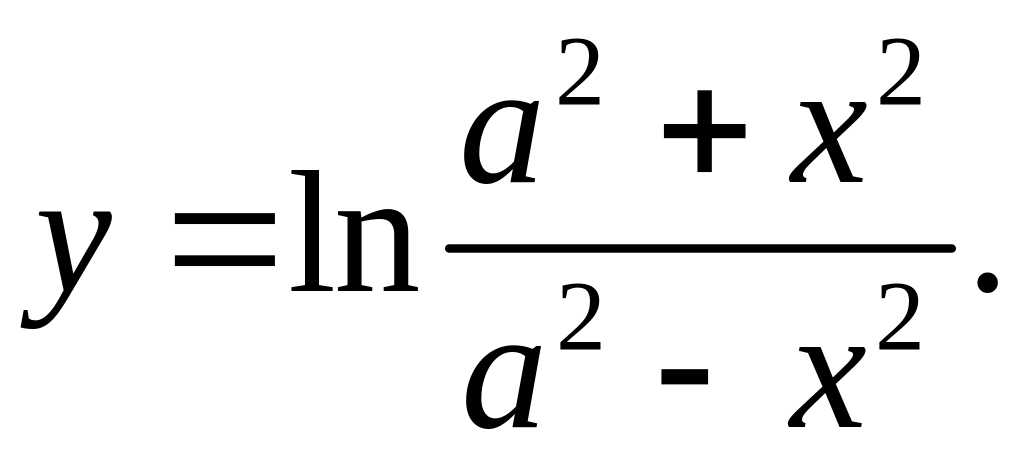 8)
8)