Причины возникновения гетероскедастичности

Гетероскедастичность может быть следствием разных причин.

1.Довольно часто гетероскедастичность возникает, если анализируемые объекты, говоря нестрого, неоднородны (сильно отличаются один от другого). Например, если исследуется зависимость прибыли предприятия от каких-либо факторов, скажем, от размера основных фондов, то естественно ожидать, что для больших предприятий колебание прибыли будет выше, чем для малых.

2.Возможны ошибки и неточности в исходных данных (ошибки измерения). Часто бóльший разброс наблюдается при больших значениях зависимой переменной. Если в данных содержится значительная ошибка, то, естественно, большим будет и отклонение, рассчитанное по ошибочным данным.

Для того чтобы избавиться от гетероскедастичности, необходимо наблюдениям с наименьшими дисперсиями придать наибольшие веса, а с максимальными дисперсиями – наименьшие. При известных для каждого наблюдения значениях дисперсии ошибок эта идея реализована в методе взвешенных наименьших квадратов, именуемом также взвешенный МНК, или обобщенный МНК.

Метод взвешенных наименьших квадратов (Взвешенный мнк)

Рассмотрим процедуру оценивания параметров для парной линейной регрессионной модели с гетероскедастичностью:

.

Преобразуем эту модель, разделив каждое наблюдение на соответствующее ему значение стандартного отклонения :

, (5.5)

где .

Для преобразованной модели (5.5) условия гомоскедастичности выполнены, так как . Применяя к (5.5) обычный метод наименьших квадратов, оценки параметров получим минимизацией суммы взвешенных квадратов отклонений:

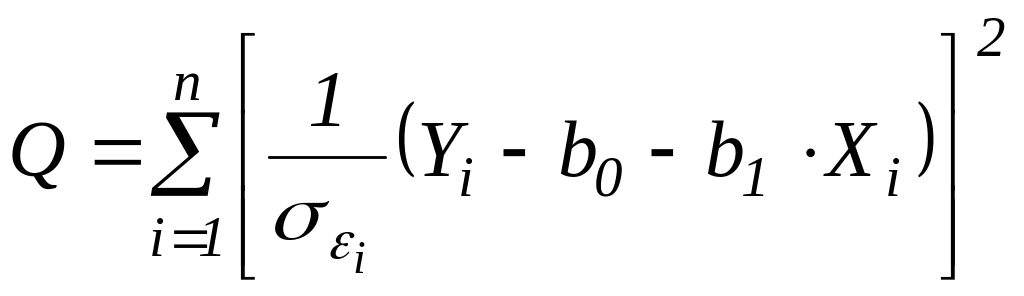. (5.6)

Содержательный смысл такого подхода.

Используя обычный МНК, мы минимизируем сумму квадратов отклонений

, (5.7)

в которую, говоря нестрого, разные слагаемые дают разный статистический вклад из-за различной дисперсии, что в конечном итоге и приводит к неэффективности МНК-оценки. “Взвешивая” каждое наблюдение с помощью коэффициента , мы устраняем такую неоднородность: наблюдениям с бóльшей дисперсией придается меньший вес . Оценки МНК параметров преобразованной модели дают непосредственно оценки исходной модели.

При использовании взвешенного МНК оценки параметров не только получаются несмещенными (они будут таковыми и для обычного МНК), но и более точными (имеют меньшую дисперсию), чем невзвешенные оценки.

Ключевым моментом при применении метода взвешенных наименьших квадратов является выбор весов.

Предпосылки к выбору весов

1. На практике дисперсии ошибок неизвестны, поэтому их заменяют оценками . Тогда модель (5.5) примет вид:

. (5.8)

После замены переменных, обычным МНК оценивается преобразованная модель вида:

, (5.9)

для которой значения преобразованных переменных вычисляются по формулам .

При оценивании параметров модели (5.9) следует иметь ввиду, что в модели (5.9) отсутствует свободный член.

2. Число оценок дисперсии ошибок равно “n”. Проблема заключается в том, что без дополнительных ограничений невозможно получить приемлемые оценки дисперсии ошибок.

Рассмотрим некоторые примеры наложения таких ограничений:

1. В первом приближении веса могут устанавливаться пропорционально остаткам невзвешенной регрессии.

2. Для экономических данных стандартные отклонения ошибок часто пропорциональны значениям объясняющей переменной , т.е. . Тогда модель (5.8) примет вид:

. (5.10)

После замены переменных, обычным МНК оценивается преобразованная модель вида:

, (5.11)

для которой значения преобразованных переменных вычисляются по формулам . Заметим, что параметры и поменялись ролями: коэффициент при будет эффективной оценкой параметра , а свободный член – эффективной оценкой параметра исходной модели.

3. При построении множественной линейной регрессии в некоторых ситуациях априорно можно считать, что ошибка прямо пропорциональна одной из независимых переменных, например :



Тогда, разделив i-тое уравнение на , i=1,...,n (n – количество наблюдений), и вводя новые независимые переменные и новую зависимую переменную , i=1,...,n, j=1,...,m (m – число независимых переменных), получим классическую регрессионную модель. МНК-оценки параметров этой модели дают непосредственно оценки параметров исходной модели.

4. Может оказаться целесообразным предположить, что не стандартные отклонения ошибок, а дисперсии ошибок пропорциональны значениям , т.е. .