7.4 Относительный метод измерения теплофизических свойств жидкостей с использованием временных интегральных характеристик температур и тепловых потоков на основе преобразования Лапласа

7.4.1 Физическая и математическая модель метода и устройства

В лабораторной практике постоянно возникает необходимость экспрессного определения комплекса теплофизических свойств жидкостей. Исходя из этого, авторами статьи [41] были разработаны нестационарный метод и устройство для измерения коэффициентов теплопроводности, температуропроводности и объемной теплоемкости плоского горизонтального слоя жидкости.

В основу разработанного метода положена физическая модель (рис. 7.2) в виде трехслойной плоской системы, на внешних границах которой при х = 0 и поддерживают постоянную температуру Т₀ , условно принимаемую за начало отсчета Т₀ = 0.

На границах между слоями 2 и 3 считаются заданными граничные условия четвертого рода [1]. На границе между слоями 1 и 2 задано граничное условие четвертого рода специального вида, учитывающее наличие в этом месте внутреннего плоского источника тепла с поверхностной плотностью q(τ).

Рис. 7.2 Физическая модель устройства

Математическая модель рассматриваемой физической системы выражается формулами:

;

;

;

;

;

;

;

;

;

.

C использованием преобразования Лапласа

математическая модель принимает вид:

; (7.19)

; (7.20)

; (7.21)

; (7.22)

; (7.23)

; (7.24)

. (7.25)

Запишем общие решения уравнений (7.19) – (7.21) в виде [16]:

; (7.26)

;

,

где С₁, С₂, С₃, С₄, С₅, С₆ – коэффициенты, определяемые с использованием граничных условий (7.22) – (7.25).

Учитывая (7.22), получаем С₂ = 0.

Если известно значение интеграла

,

тогда из (7.26) следует

.

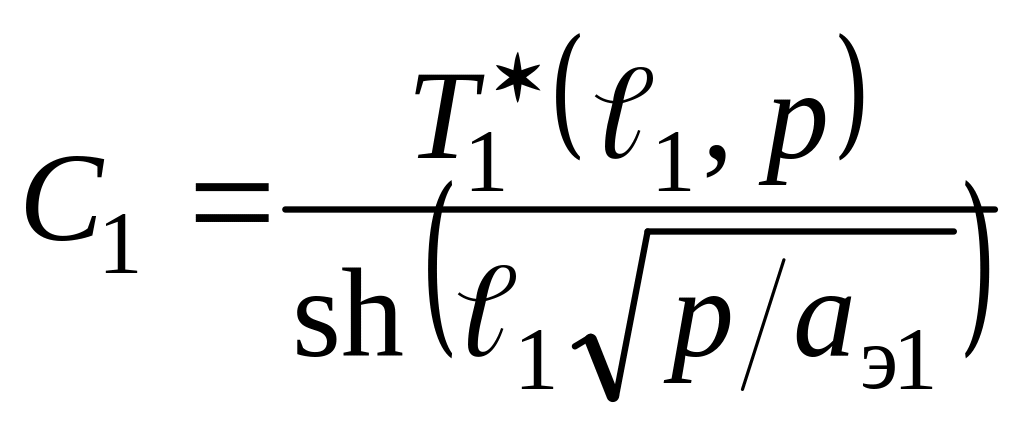Постоянные С₃, С₄ определяем как решение системы алгебраических уравнений

(7.27)

получающейся с использованием граничных условий (7.23). В результате решения системы уравнений (7.27) находим, что значения

;

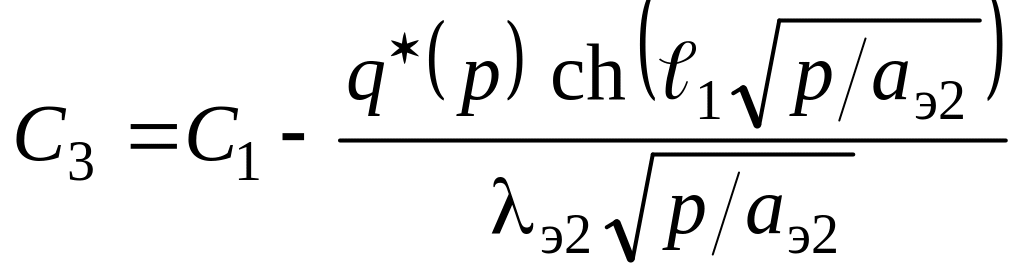
зависят от параметра р преобразования Лапласа.

С использованием обозначений

на основе граничных условий (7.24), (7.25) получаем систему уравнений

откуда

;

;

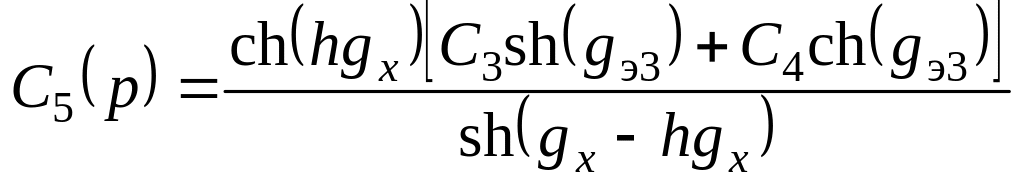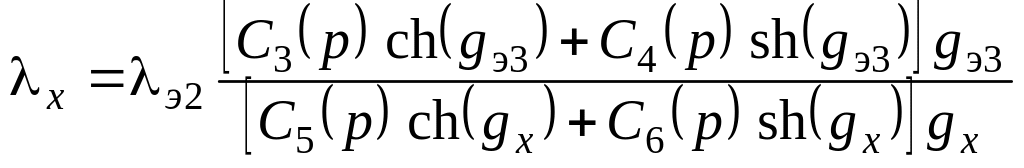. (7.28)

Для определения значения неизвестного g_x зададимся двумя значениями параметра преобразования Лапласа р₁ = р и р₂ = kp, где k – постоянная величина. Тогда в дополнение к выражению (7.28) получим

. (7.29)

Поделив (7.28) на (7.29), получаем уравнение для вычисления значения параметра g_x

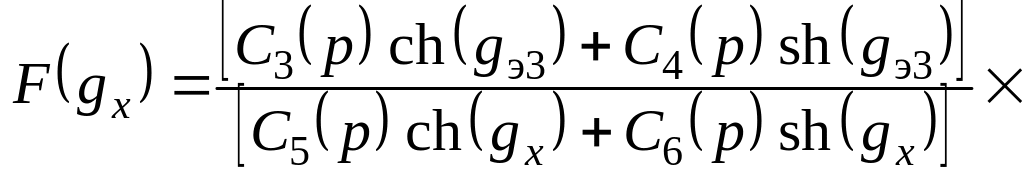
. (7.30)

Вычислив значение g_x как корень уравнения (7.30), коэффициент теплопроводности рассчитаем по (7.28), коэффициент температуропроводности определим из выражения

. (7.31)

Коэффициент объемной теплоемкости жидкости вычислим по формуле

. (7.32)

С целью упрощения алгоритма обработки экспериментальной информации уравнение (7.30) преобразуем к виду

, (7.33)

где

; ;

.