Задача 4. Графическое решение задачи линейного програмирования.
Для изготовления двух видов продукции используется три вида сырья. При производстве единицы продукции первого вида затрачивается 5 кг сырья первого вида, 10 кг сырья второго вида и 10 кг сырья третьего вида. При производстве единицы продукции второго вида затрачивается 3 кг сырья первого вида, 12 кг сырья второго вида и 8 кг сырья третьего вида. Запасы сырья первого вида составляют 220 кг, второго – 220 кг, третьего – 240 кг. Прибыль от реализации единицы продукции первого вида составляет 16 ден. ед., прибыль от реализации единицы продукции второго вида составляет С2 14 ден. ед.
Определить оптимальный план выпуска продукции(количество выпускаемой продукции округлить до целого числа), чтобы прибыль от реализации была максимальной.
Пусть x1 – оптимальное количество выпускаемого продукта 1, x2 – продукта2.
Запишем целевую функцию:
16 x1+14 x2 – max.
И ограничения:
5 x1 + 3 x2 <= 220
10 x1 + 12 x2 <=220
10 x1 + 8 x2 <=240
x1>=0
x2>=0
Нарисуем ОДЗ системы неравенств ограничений в 1-ом квадранте:
Уравнения прямых x2 (x1)
x2=220/3-(5/3) x1.
x2=220/12-(10/12) x1
x2=30-(10/8) x1
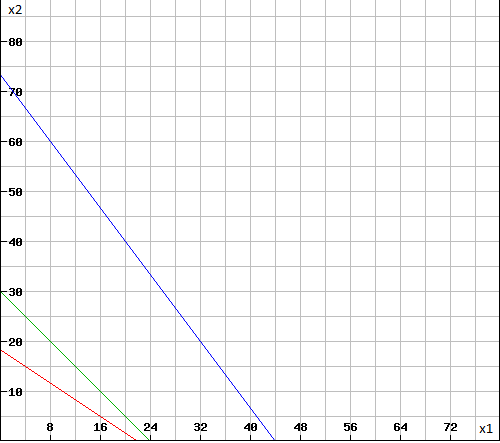
Очевидно, ОДЗ – это треугольник ABC:
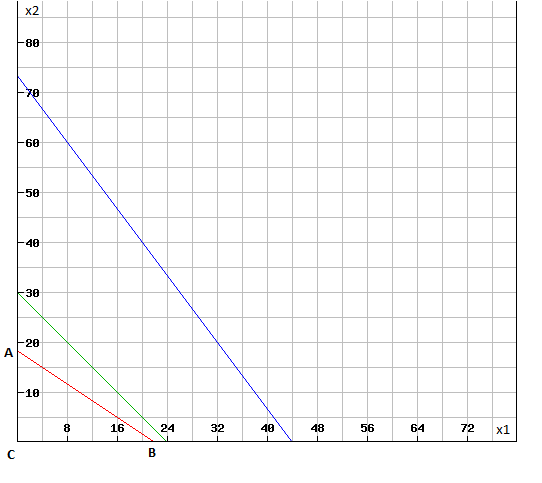
Целевая функция 16 x1+14 x2.
Нормаль к ней – вектор (16,14).
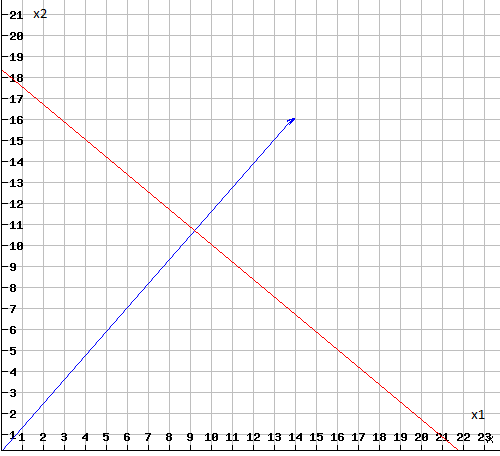
Двигаем целевую функцию вдоль нормали для нахождения максимума:
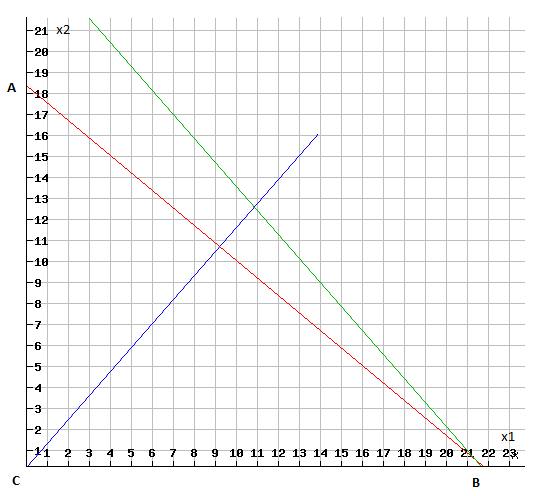
Очевидно, максимум в точке оптимума B (22,0). Следовательно, в оптимуме x2=0.
Из ограничения (красная линия):
x2=220/12-(10/12) x1 =>
x1=22.
Тогда максимальное значение целевой функции:
16 x1+14 x2=352.
Ответ: Оптимальный план выпуска продукции с целью максимизации прибыли: выпустить 22 единицы товара первого вида, и не выпускать товар второго вида. При оптимальном плане прибыль составит 352 ден. ед.
Задача 4. Симплекс-метод
Запишем ограничения в канонической форме, включив базисные переменные.
5 x1+3 x2+ x3=220
10 x1+12 x2+ x4=220
10 x1+8 x2+ x5=240
Целевая функция f(x)=16 x1+14 x2.
Составим симплекс-таблицу для целевой функции f(x).
Базис |
План |
x1 |
x2 |
x3 |
x4 |
x5 |
x3 |
220 |
5 |
3 |
1 |
0 |
0 |
x4 |
220 |
10 |
12 |
0 |
1 |
0 |
x5 |
240 |
10 |
8 |
0 |
0 |
1 |
f(x) |
0 |
-16 |
-14 |
0 |
0 |
0 |
Найдем генеральный элемент. Столбец – максимум модуля коэффициента в строке f(x) : max{16,14}=16, столбец x1. Строка – минимум отношения плана к значению в ячейке столбца: min{220/5,220/10,240/10}=22 – строка 2. Тогда выделим базисную переменную x1 и запишем вторую симплекс-таблицу:
В строке с x1 разделим все коэффициенты на 10, чтобы сделать x1 базисной (с коэффициентом единица).
Базис |
План |
x1 |
x2 |
x3 |
x4 |
x5 |
x3 |
|
|
|
|
|
|
x1 |
22 |
1 |
1,2 |
0 |
0,1 |
0 |
x5 |
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
Выразили x1:
x1=22-1,2 x2-0,1 x4
Подставим x1 в f(x):
F(x)=352-5,2 x2-1,6 x4. Внесем в симплекс-таблицу:
Базис |
План |
x1 |
x2 |
x3 |
x4 |
x5 |
x3 |
|
|
|
|
|
|
x1 |
22 |
1 |
1,2 |
0 |
0,1 |
0 |
x5 |
|
|
|
|
|
|
f(x) |
352 |
0 |
5,2 |
0 |
1,6 |
0 |
Все коэффициенты в строке f(x) неотрицательны, значит оптимум найден.
Ответ: x1=22, x2=0, максимум f(x) – 352.