2. Квантование отсчетов непрерывных сигналов. Средняя мощность шумов квантования. Определение необходимого числа шагов для линейной шкалы квантования.

С целью уменьшения эффекта накапливания помех в СП данных широко использ метод регенерации сигналов, искаженных шумом. Если реализ приним сигнала находится в зоне правильн приема, то выносится опред решение, в соответств с котор формир элемент сигнала, очищенный от шумов. Указанный способ устранения шумов работоспособен только при перед цифров сигналов, т.е сигн с конечным числом состояний. Воспользуемся данным методом для перед отсчетов непрерыв первич сигналов. В этом вся область допуст мгновенных значений отсчетов а(it) делится на М разреш или квантованных уровней (рис 1(а)) и каждый раз при перед очередн отсчета его значение округл до ближайшего разреш уровня. При этом, возникает ошибка округления(квантовния), (рис 1 (б))

_кв(it)=а(it)-а_кв(it)

разность  м/д двумя соседн уровн квантования назыв шагом квантов. Поскольку на приеме наблюд не истенные значения, а квантованные

а_кв(it)= а(it)- _кв(it), то на вых ФНЧ приема вместе с полезным сигналом а(t) будет присутствовать шум квантования _кв. введение квантованных сигналов пораждает уже на передаче шум, эффективная мощн которого не должна превышать допустимого значения для стандартных каналов ТЧ.

Средн мощн шумов квантов.

В предположении идеальной передачи квантованного сигнала помехозащищенность А_{з кв} будет опред только шумами квантования, т.е А_{з кв}=10lg(P_c/P_кв),

где Р_с-средняя мощн сигн, Р_кв-средн мощн шума квантов. Условно квантов можно осущ путем пропуск отсчет сигн через четырехполюсник-квантователь с кусочно-ломанной амплитудной хар-ой (рис 2 (а)). амплитудная хар-ка квантов а_кв=F(а) м/б предст в виде суммы идеальн лин-ой хар-ки, опред-ей искажение сигнала(рис 2(б)). хар-ка квантов имеет 2 участка: зону квант и зону огранич. В зоне квант погрешн _кв всегда наход в пределах -/2.. /2. в зоне огранич, когда а>U_огр (U_огр-порог огранечения квантователя), погрешность _огр=а- U_огр пропорциональна значению квантуемого отсчета. Поэтому результирующий шум на выходе канала при передаче квантованных значений случайного сигнала будет состоять из 2 слагаемых- шума квант и шума ограничения.при малых средн мощн(уровнях) сигнала, т.е при узкой плотности распер мгновенных значений(кривая 1 на рис в), все его реализации наход в пред зоны квантования, а при больш средн мощн сигн(кривая 2 на рис г) значит часть его реализации попадает в зону ограничения. Опред мощн шума квант, пологая, что плотность распред w(a) мгновенных значений квант сигн известна. При дост больш числе уровн-й квант М можно счит, что плотн распред w(a)_I в пред кажд i-го участка квантов равномерна, т.е имеет вид прямоугольн с ширин  и ординатой w(a_i). Поэт дисперсия шума квантов для i-го участка опред известн соотнош

Но в силу сделанного допущения плотн распр w(a) в пред кажд i-го участка постоянна,тюе не завист от а и приблизит равна w(a_i). Тогда последн интеграл после замены переменных (а-а_i) привод к виду

Где р_i=w(а_i)_i- вероятн попод сигн в i-ю зону квант. Суммарн дисперс буд опред суммой дисперсией в каждой зоне квантов или

При равномерн квантов, когда все шаги _i одинаковы, а полная вероятность р_i=1, получаем

Из последней формулы следует, что при равномерн квантов дисперсия ²_кв завист лишь от шага квантован  и не завис от уров сигнала. При заданном динамическом диапаз сигн велич  однозначно опред необходимое число уровней квантов М.

Рис. 1.К понятию квантования сигналов по уровню.

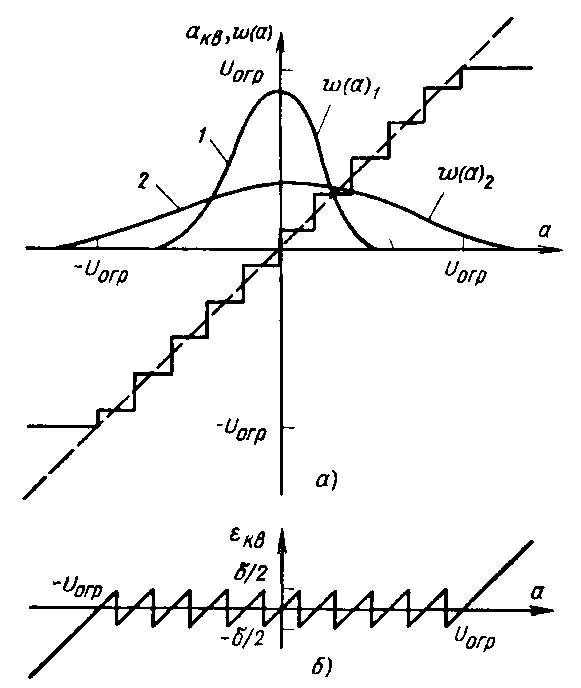
Рис 2. К определению мощности шумов квантования и ограничения.

Определение необходимого числа шагов для линейной шкалы квантования.

На рис 3 приведена зависим вероятн ошибки от числа уровней М при отношен сигн-помеха равном 20дБ.

Эксперимент-но установл, что кач-во перед непр сигн методом кванто-ой АИМ будет удовлетворительным, если вероятн ошибочной регистрации передов уровня не привеш 10^-8 на весь тракт. Ошибки возник в кажд пункте регенер, практич можно счит независимыми. Поэтому при числе регенераторов в тракте , равном К, вероятн ошибки на кажд регенер не долж превыш 10^-8/К. из рис след, что обеспеч так вер ошиб в случ идеальн хар-к тракта можно только при М<32, но тогда будут большие шумы квантов. Если же в тракте перед есть АЧИ и ФЧИ , то даже при любых малых их значен вер ошиб не будет равна 0 в отсут помех в тракте. Следов, устр эффект накапл помех в тракте за счет перед сигн метод квант АИМ невозможно.

Рис 3. Зависимость вероятности ошибки от числа уровней квантования.