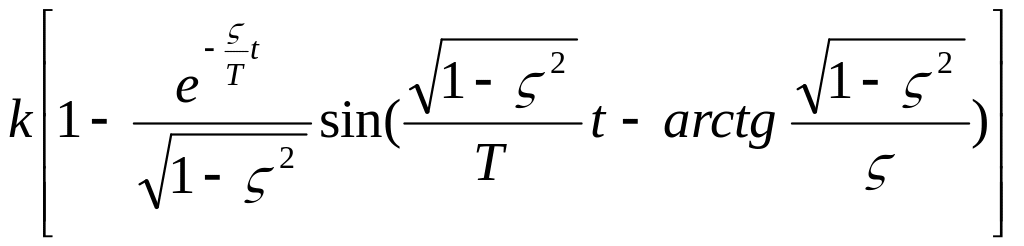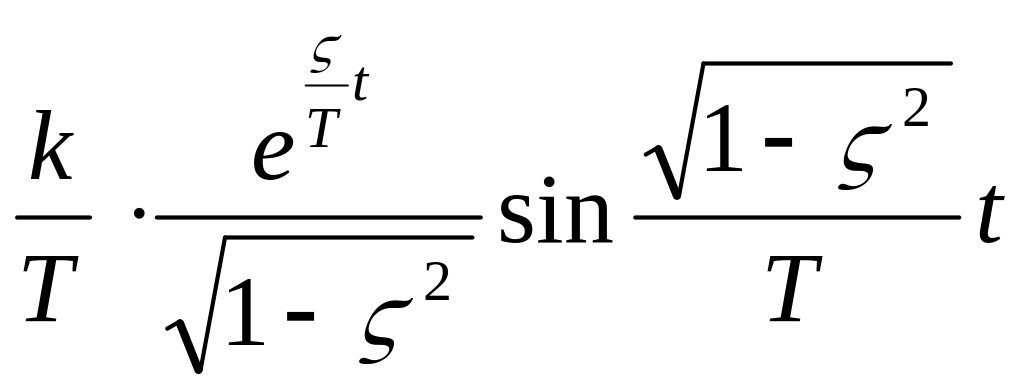2.Елементарні (типові) динамічні ланки, їхні рівняння й динамічні функції

Під звичайними елементарними (типовими) динамічними ланками розуміють ланки, рух яких описується лінійними диференціальними рівняннями не вище другого порядку з позитивними коефіцієнтами.

1. Рівняння й передатні функції Таблиця 1.3

№ п. п.	Ланка	Рівняння
1	Підсилювальне
2	Інтегруюче
3	Аперіодичне: стійке нестійке
4	Коливальне: стійке нестійке консервативне
5	Що диференціює: ідеальне першого порядку другого порядку
6	Запізніле

2.Частотні функції

№ П.П.	Ланка
1	Підсилювальне		0
2	Інтегруюче
3	Аперіодичне: стійке нестійке
4	Коливальне: стійке нестійке консервативне		0 при при
5	Що диференціює: ідеальне першого порядку другого порядку
6	Запізніле		-

3. Тимчасові функції

№ п.п.	Ланка
1	2	3	4
1	Підсилювальне		при 0 при
2	Інтегруюче
3	Аперіодичне: стійке нестійке
4	Коливальне: стійке нестійке консервативне
5	Що диференціює: ідеальне першого порядку другого порядку
6	Запізніле

Позначення, прийняті в таблиці:

-коефіцієнт перетворення;

T - постійна часу;

- коефіцієнт загасання;

1(t) -одиничний перепад (одинична східчаста функція);

одиничний імпульс (дельта-функція).

До звичайних динамічним ланками ставляться: підсилювальне ( безінерційне, пропорційне), що інтегрує, стійке аперіодичне, стійке коливальне, ідеальне що диференціює, що диференціює першого порядку й диференціює другого ланки.

До особливих елементарних ланки лінійних САУ ставляться: не мінімально-фазові ланки; нестійкі ланки; ланки з розподіленими параметрами; ірраціональні, трансцендентні.

Не мінімально - фазові ланки мають передатну функцію з нулями в правій напівплощині. Нестійкі ланки мають полюса в правій напівплощині. Ірраціональні ланки описуються ірраціональними передатними функціями, а трансцендентні- трансцендентними передатними функціями.

Динамічні функції звичайних ланок і деяких типів особливих ланок наведені в таблиці 1.

Структурні схеми САУ

Структурною схемою називається графічне зображення елемента або САУ, що відображає систему диференціальних рівнянь, що описують процеси керування в цих елементах або САУ.

Умовні зображення елементів структурних схем наведені на мал.1.12.

Методика складання структурних схем

Загальне правила, які повинні виконуватися при складання структурних схем:

1. структурна схема повинна обов'язково мати вхідні й вихідні зовнішні зв'язки, що задають із фізичних міркувань;

2. кожен вхідний сигнал, що є незалежною функцією часу, повинен мати тільки вхід у структурну схему;

3. вихідний сигнал може замикатися усередині структурної схеми й має вихід виді відгалуження (система, замкнута по вихідному сигналі) або не замикатися усередині структурної схеми (система, замкнута по вихідному сигналі);

4. всі внутрішні зв'язки, обумовлені системою рівнянь, повинні обов'язково мати входи й виходи.

Послідовність складання структурної схеми САУ по заданій системі диференціальних рівнянь її окремих елементів наступна:

а) система диференціальних рівнянь записується в операторной формі;

б) для кожного рівняння системи умовно вибираються вхідна й вихідна величини;

в) кожне рівняння вирішується щодо вихідної величини або члена, що містить її старшу похідну;

г) будуються графічні відображення кожного з диференціальних рівнянь;

д) будується загальна структурна схема як сукупність графічних відображень кожного диференціального рівняння.

Рис 1.12 Умовні позначки елементів структурних схем

Динамічна ланка Підсумовуюча ланка (суматор

Функціональна ланка

Множна ланка

Приклад 1.7. Побудувати структурну схему двигуна постійного струму з незалежним порушенням при керуванні по ланцюзі якоря (мал. 1.13), якщо його рух може бути записано системою лінеаризованих рівнянь (знаки збільшень опущені):

(1.17)

(1.18)

(1.19)

де U(t)-напруга прикладене до ланцюга якоря;

i(t)- струм у ланцюзі якоря;

R;L -активний опір й індуктивність ланцюга якоря;

-коефіцієнт э.д. с. двигуна;

w(t)-кутова швидкість обертання ротора двигуна;

обертаючий момент двигуна

коефіцієнт моменту двигуна;

момент опору від сил сухого тертя;

коефіцієнт грузлого тертя;

J- момент інерції обертаючих частин.

Як вихідна величина двигуна приймається кутова швидкість

Рис.1.13 Принципова схема двигуна постійного струму наприклад 1.7.

Рис. 1.14 Структурна схема, що відповідає (1.22).

Рис .1.15 Структурна схема, що відповідає рівнянню (1.23)

Рішення:

1. рівняння (1.17)-(1.19) в операторній формі приймуть вид:

(1.20)

(1.21)

2. вхідною величиною рівняння (1.20) є напруга U, у якості вихідної приймемо струм i . Вхідною величиною для рівняння (1.21) буде величина I , вихідний - кутова швидкість w;

3. вирішуємо рівняння (1.20) щодо першої похідної струму i і рівняння (1.21) щодо першої похідної швидкості w. Одержимо :

(1.22)

(1.23)

4. будуємо схему, що відповідає рівнянню (1.22),- мал. 1.14; будуємо схему, що відповідає рівнянню (1.23),- мал. 1.15;

5. поєднуємо мал. 1.14 й 1.15, замикаємо зворотний зв'язок через ланку й одержуємо структурну схему двигуна (мал. 1.16).

Рис. 1.16 Структурна схема наприклад 1.7.