2.4 Лабораторная работа № 4

Определение вариации социально-экономических показателей

Цель работы: научиться рассчитывать, анализировать и делать выводы по численному значению абсолютных и относительных показателей вариации: размаху вариации, среднему линейному отклонению, дисперсии, среднему квадратическому отклонению, коэффициенту осцилляции, линейному коэффициенту вариации и коэффициенту вариации.

Общие сведения

К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.

Размах вариации – показатель, определяющий насколько велико различие между единицами совокупности, имеющими наибольшее и наименьшее значение признака. Зависимость для его расчета имеет вид

.                (5)

Среднее линейное отклонение - показатель, отражающий типичный размер признака. Расчетная зависимость для его определения имеет вид

а) простое среднее линейное отклонение для не сгруппированных данных

, (6)

где n – число наблюдений признака.

б) взвешенное среднее линейное отклонение для интервального вариационного ряда

.              (7)

Рассмотрим пример расчета взвешенного среднего линейного отклонения  по исходным данным, приведенным в таблице 3.    

Таблица 3 –   Распределение населения Пензенской области по возрастным группам на начало 2005 года (без возрастной группы 70 лет и старше)

Возрастной интервал,	Численность  населения, тыс. чел,
0-4	56,7
5-9	57,3
10-14	80,6
15-19	116,6
20-24	104,7
25-29	97,2
30-34	94,7
35-39	93,2
40-44	115,5
45-49	121,4
50-54	111,3
55-59	86,7
60-64	61,4
65-69	84,2

Для  удобства и наглядности вычислений преобразуем  таблицу 3 к виду таблица 4.

Таблица 4 – К расчету среднего линейного отклонения       

Возрастной интервал,	Численность  населения, тыс. чел.,
0-4	56,7	2	113,4	1904,4
5-9	57,3	7	401,1	1638,0
10-14	80,6	12	967,2	1901,1
15-19	116,6	17	1982,2	2167,3
20-24	104,7	22	2303,4	1422,6
25-29	97,2	27	2624,4	834,7
30-34	94,7	32	3030,4	339,7
35-39	93,2	37	3448,4	131,7
40-44	115,5	42	4851	740,7
45-49	121,4	47	5705,8	1385,5
50-54	111,3	52	5787,6	1826,7
55-59	86,7	57	4941,9	1856,5
60-64	61,4	62	3806,8	1621,7
65-69	84,2	67	5641,4	2645,0
Итого	1281,5		45605	20415,6

В соответствии с данными таблицы 4 имеем:

Вывод.  В начале 2005 года в распределении населения Пензенской области  по возрастным группам (без учета возрастной группы 70 лет и старше)  наиболее  типичным являлся возраст  равный 16 годам.

Среднее линейное отклонение  позволяет определить  обобщенную характеристику  колеблемости   признака в совокупности, однако при его исчислении приходится иметь дело с  модулями  алгебраических выражений, что  при упрощенных конечных выражениях может приводить к ошибкам и неточностям. Более удобно использовать показатели вариации, найденные с использованием  вторых степеней отклонений.

Полученная  при этом  мера вариации называется  дисперсией ( ), а корень   квадратный из  дисперсии – средним квадратическим отклонением  ( ).

Дисперсия  - средняя величина квадратов отклонений  индивидуальных значений признака  от их средней величины.

Рабочие зависимости для расчета дисперсии имеют вид:

а) простая дисперсия для не сгруппированных данных

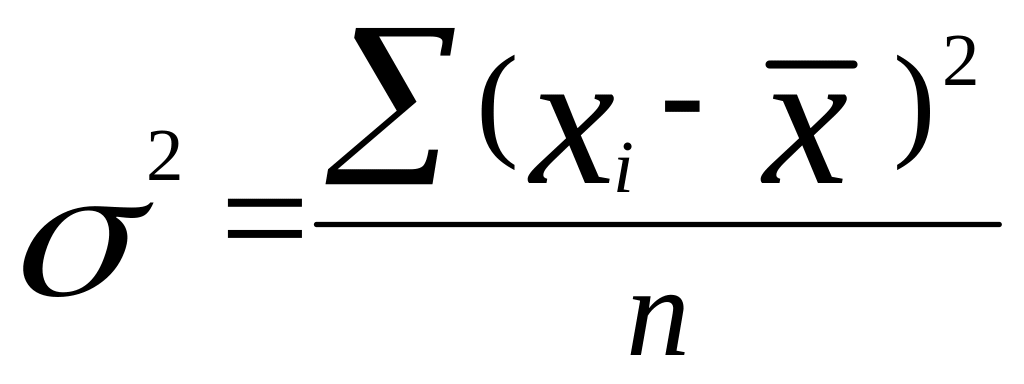, (8)

б) взвешенная дисперсия для интервального вариационного ряда

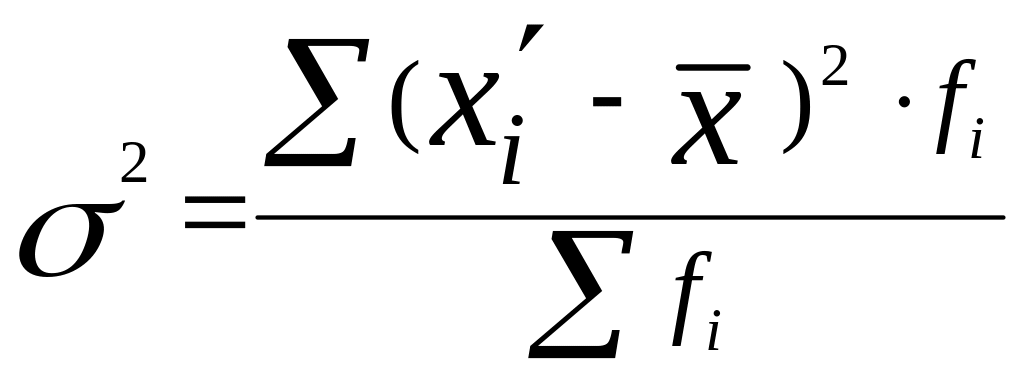.                     (9)

Среднеквадратическое отклонение – корень квадратный из дисперсии.

а) Простое среднеквадратическое отклонение для не сгруппированных данных

, (10)

б) Взвешенное среднеквадратическое отклонение для интервального вариационного ряда

.                 (11)

Среднеквадратическое отклонение  выражается в тех же единицах измерения, что и значение признака.

Дисперсия и среднее квадратическое отклонение определяются по зависимостям

, (12)

. (13)

Для удобства и наглядности вычислений преобразуем таблицу 4 к виду таблица 5.

Таблица 5 – К расчету дисперсии

Возрастной интервал, хi	Численность населения, тыс. чел., fi
0-4	56,7	2	63963,3
5-9	57,3	7	46827,2
10-14	80,6	12	44842,3
15-19	116,6	17	40283,4
20-24	104,7	22	19328,9
25-29	97,2	27	7167,5
30-34	94,7	32	1218,6
35-39	93,2	37	186,0
40-44	115,5	42	4749,8
45-49	121,4	47	15812,6
50-54	111,3	52	29982,0
55-59	86,7	57	39752,6
60-64	61,4	62	42834,8
65-69	84,2	67	83085,5
Итого	1281,5		440034,6

В соответствии с данными таблицы 5 имеем

Вывод. Анализ численного значения дисперсии и среднего квадратического отклонения показывает, что в исследуемом интервальном вариационном ряду наблюдается значительный разброс признака относительно его среднего значения.

Относительные показатели вариации   используются для  сравнения  колеблемости  различных признаков  в одной и той же совокупности,  либо при сравнении  колеблемости  одного и того же признака в разных совокупностях. Базой структуры этих показателей является  средняя арифметическая.

К относительным показателям вариации относятся.