В отведенных ячейках строки 43 подсчитываем числовые характеристики:
выборочную среднюю
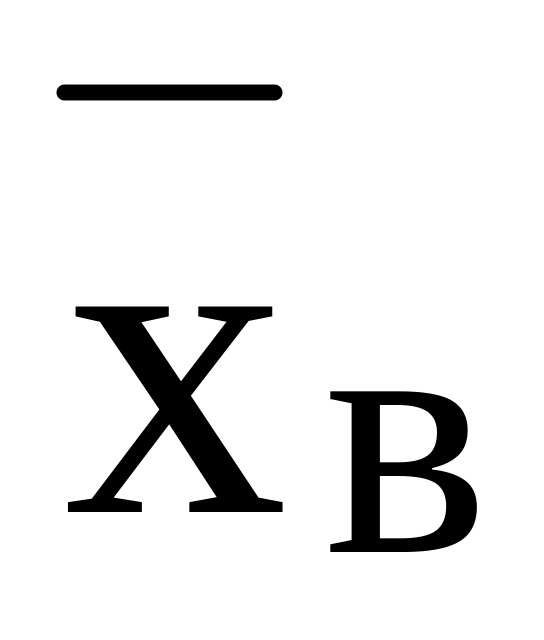(«Мастер
Функций»,
категория
«СТАтистиЧеские»,
функция
СРЗНАЧ
). В
качестве аргумента выделяем массив
исходных данных
столбец A6:A35 или лучше вызываем
клавишей F3 его имя
"выборка";
статистическую моду m o* ( там же, функция МОДА );
статистическую медиану m e* ( там же, функция МЕДИАНА );
_ _ _ _ _ _ _ _
среднее абсолютное отклонение ( там же, функция СРОТКЛ );
выборочную дисперсию Dв ( там же, функция ДИСПР );
выборочное стандартное (среднеквадратическое) отклонение
(категория «МАТЕМАТиЧеские», функция КОРЕНЬ );
коэффициент вариации ( программируем формулу
).
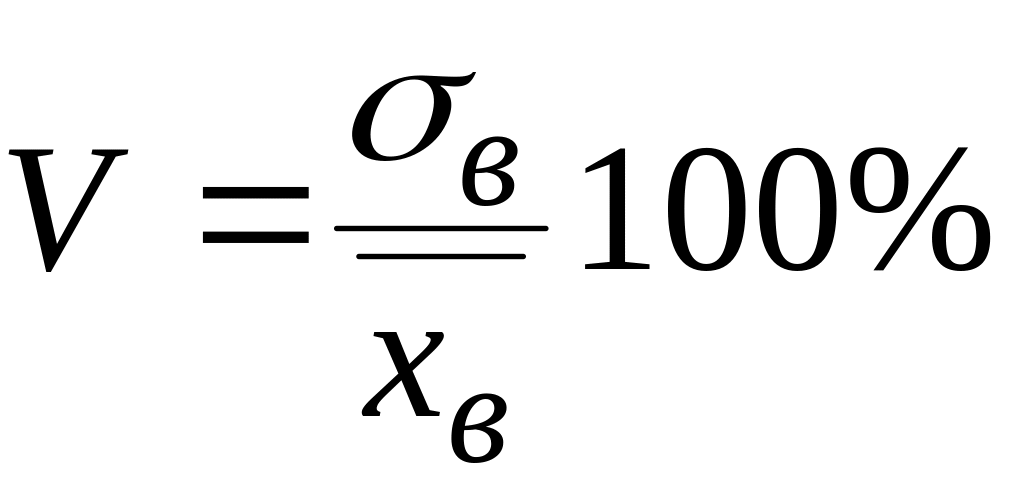5. Точечные оценки параметров распределения
Найденные числовые характеристики выборки используем для оценки параметров распределения:
Статистической оценкой для математического ожидания
служит выборочная средняя:
.
Статистической оценкой для дисперсии
служит исправленная выборочная дисперсия:
.
Статистической оценкой для стандартного отклонения
служит исправленное выборочное стандартное отклонение:
.
Как это сделать в EXСEL
Для статистических оценок параметров распределения отведены ячейки строки 47 :
оценка для математического ожидания m x :
;
В ячейку D47 просто копируем содержимое ячейки B43 ( =B43).
для теоретической дисперсии D x :
;
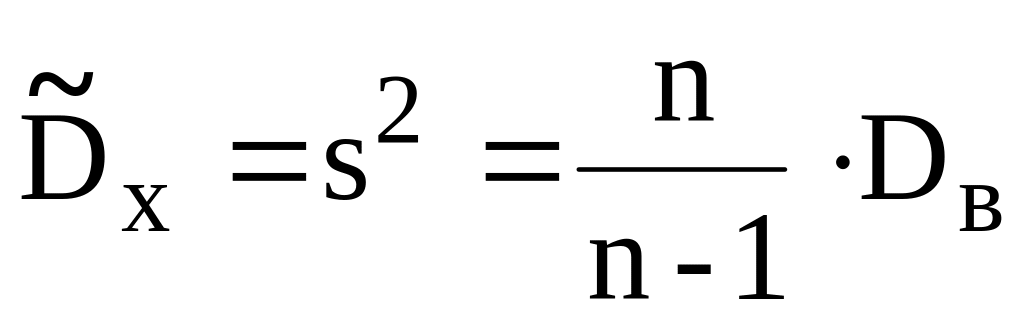В ячейке E47 "исправляем" выборочную дисперсию, програмируя формулу ( =F43*объем/(объем-1) ) ;
для теоретического стандартного отклонения
:
;
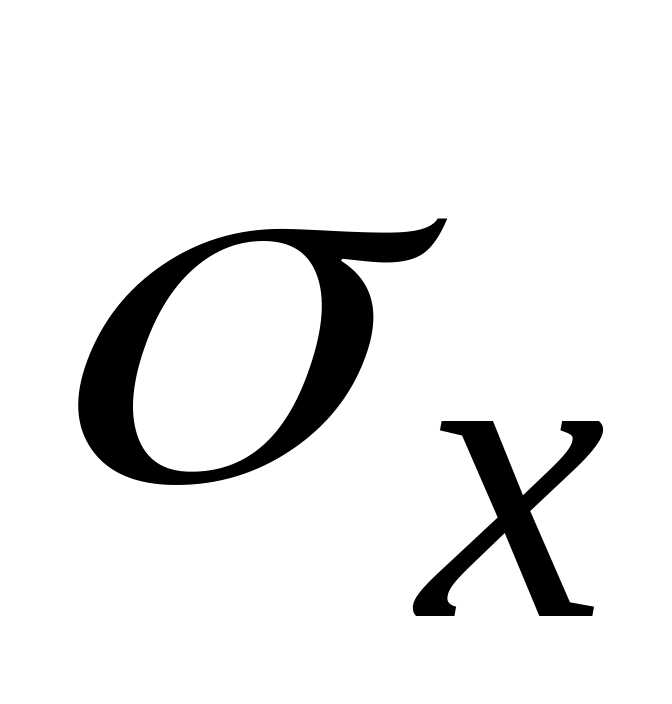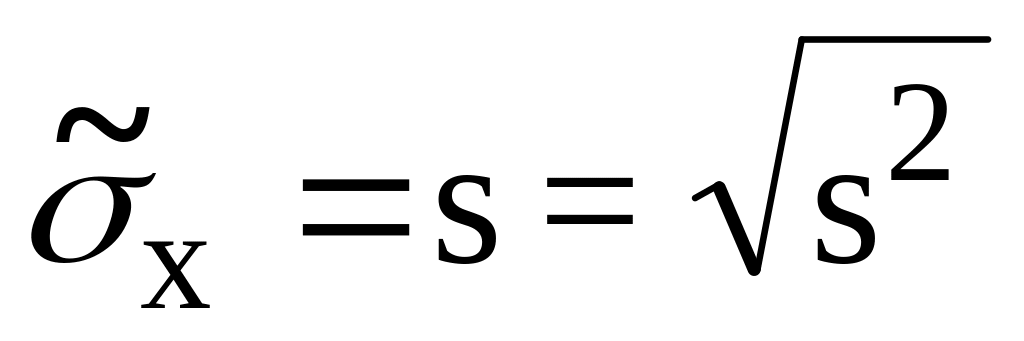В ячейке F47 извлекаем корень из исправленной дисперсии :
( = КОРЕНЬ(E47) )
Сохранить файл на электронном носителе.