УТВЕРЖДАЮ     

Ректор университета

__________А.В. Лагерев

“____”___________2012 г.

Математический анализ

Методические указания к изучению дисциплины

для студентов заочной формы обучения направлений

230100.62 «Информатика и вычислительная техника»

и 230400.62 «Информационные системы и технологии»

(2 семестр)

Брянск 2012

УДК 516.1/4

Математический анализ [Текст]+[Электронный ресурс]: методические указания к изучению дисциплины для студентов заочной формы обучения направлений 230100.62 «Информатика и вычислительная техника» и 230400.62 «Информационные системы и технологии» (2 семестр). – Брянск: БГТУ, 2012. – 23 с.

Разработал: А.П. Мысютин, к.т.н., доц.

Рекомендовано кафедрой “Высшая математика” БГТУ

(протокол №9 от 31.05.2012)

Предисловие

Студенты первого курса заочной формы обучения направлений 230100.62 «Информатика и вычислительная техника» и 230400.62 «Информационные системы и технологии» во втором семестре по дисциплине «Математический анализ» должны выполнить две контрольные работы. В первой работе представлены задания по разделам «Введение в анализ» и «Дифференциальное исчисление функций одной переменной», а во второй − по разделу «Интегральное исчисление функций одной переменной». В соответствии с учебными планами промежуточная аттестация проводится в форме экзамена для студентов направления «Информационные системы и технологии» и в форме зачета для студентов направления «Информатика и вычислительная техника».

Существует много учебных пособий, в которых подробно рассмотрены перечисленные разделы высшей математики. К ним относятся:

1. Пискунов, Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. – М.: Интеграл-Пресс, 2009. – Т. 1. – 416 с.

2. Бугров, Я.С. Высшая математика. Дифференциальное и интегральное исчисление. Т.2./ Я.С. Бугров, С.М. Никольский.– М.: Дрофа, 2007. – 512 с. – (Сер. Высшее образование. Современный учебник).

3. Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. − М.: Айрис-пресс, 2010. – Ч. 1. − 288 с.

4. Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова, С.П. Данко. – М.: Оникс, 2008. – 816 с.

5. Шипачев, В.С. Математический анализ. Теория и практика / В.С. Шипачев. – М.: Дрофа, 2006. – 352 с.

6. Бермант, А.Ф., Араманович, И.Г. Краткий курс математического анализа / А.Ф. Бермант, И.Г. Араманович. – М.: Лань, 2009.

7. Минорский, В.П. Сборник задач по высшей математике / В.П. Минорский. – М.: Изд-во физ.-мат. лит-ры, 2010. – 336 с.

Считая базовым учебник [3], укажем темы, которые необходимо изучить студенту для успешного выполнения контрольных работ.

Контрольная работа №1

Тема 1. Множества. Действительные числа

1. Основные понятия. Литература: [3], §13, п. 13.1.

2. Числовые множества. Множество действительных чисел. Литература: [3], §13, п. 13.2.

3. Числовые промежутки. Окрестность точки. Литература: [3], §13, п. 13.3.

Тема 2. Функции

1. Понятие функции. Литература: [3], §14, п. 14.1.

2. Числовые функции. График функции. Способы задания функций. Литература: [3], §14, п. 14.2.

3. Основные характеристики функции. Литература: [3], §14, п. 14.3.

4. Обратная функция. Литература: [3], §14, п. 14.4.

5. Сложная функция. Литература: [3], §14, п. 14.5.

6. Основные элементарные функции и их графики. Литература: [3], §14, п. 14.6.

Тема 3. Последовательности

1. Числовая последовательность. Литература: [3], §15, п. 15.1.

2. Предел числовой последовательности. Литература: [3], §15, п. 15.2.

3. Предел монотонной ограниченной последовательности.

Число е. Натуральные логарифмы. Литература: [3], §15, п. 15.4.

Тема 4. Предел функции

1. Предел функции в точке. Литература: [3], §16, п. 16.1.

2. Односторонние пределы. Литература: [3], §16, п. 16.2.

3. Предел функции при 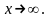Литература: [3], §16, п. 16.3.

4. Основные теоремы о пределах. Литература: [3], §17, п. 17.3.

5. Замечательные пределы. Литература: [3], §17, п. 17.5, 17.6.

Тема 5. Непрерывность функций

1. Непрерывность функции в точке. Литература: [3], §19, п. 19.1.

2. Непрерывность функции в интервале и на отрезке. Литература: [3], §19, п. 19.2.

3. Точки разрыва функции и их классификация. Литература: [3], §19, п. 19.3.

4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций. Литература: [3], §19, п. 19.4.

Тема 6. Производная функции

1. Определение производной, ее механический и геометрический смысл. Уравнение касательной и нормали к кривой. Литература: [3], §20, п. 20.2.

2. Производная суммы, разности, произведения и частного функций. Литература: [3], §20, п. 20.4.

3. Производная сложной и обратной функций. Литература: [3], §20, п. 20.5

4. Таблица производных. Литература: [3], §20, п. 20.8.

5. Дифференцирование неявных и параметрически заданных функций. Литература: [3], §21.

6. Производные высших порядков явно заданной функции. Литература: [3], §23, п. 23.1.