Задание 3

Fs=151.2 KHz

F s=158.4 KHz

Fs=165.6 KHz

Fs=172.8 KHz

Вывод: с увеличением частоты дискритизации количество выборок на период возрастает, следовательно сигнал представлен более точно. На фазовом графике появилась еще одна частота в следствие отхода от минимальной частоты дискритизации.

Задание 4

Fs=144*8=1152 KHz

Fs=144*10=1440 KHz

Вывод: еще большее увеличение частоты повысило точность представления исходного сигнала.

Задание 5

% ПРОГРАММА ИССЛЕДОВАНИЯ ХАРАКТЕРИСТИК ЦИФРОВЫХ СИГНАЛОВ

%(ГАРМОНИЧЕСКИХ, КВАНТОВАННЫХ ПО УРОВНЮ)

clear; % очищаем память

t0=0; % начало сигнала в момент времени 0 с.

Fs=2304e3; % частота дискретизации 20 КГц

N=1024; % общее число отсчетов

t=t0:1/Fs: (N-1)*1/Fs; % вектор дискретных значений времени t(n)

f=72e3 % частота несущей (гармонического сиогнала)

fi0=0 % начальная фаза сигнала

n=1:1:numel(t); % определение размера массива результатов по размеру массива отсчетов времени

t(n)=(n-1)*(1/Fs); % вычисление массива отсчетов времени

A(n)=24; % определение вектора (массива)амплитуд

u0(n)=A(n).*cos(2*pi*f*t(n)+fi0) %вектор дискретных значений сигнала

u=uencode(u0,3) %имитация эффекта конечной разрядной сетки (квантования по уровню)

axis tight; % масштаб такой, чтобы вошел весь

% диапазон значений по обеим осям

plot(t,u); % график сигнала

title('Signal u(n)'); % заголовок графика

xlabel('time, t=nT=n/Fs (tmax=NT), [s]'); % надписи по горизонтальной оси

ylabel('u(n), [V]'); % надписи по вертикальной оси

figure % создание нового окна

stem(t*Fs,u); % график сигнала в виде "стебельков"

title('Signal u(n)'); % заголовок графика

xlabel('time, n (n max=N), [pcs]'); % надписи по горизонтальной оси

ylabel('u(n), [V]'); % надписи по вертикальной оси

Nfft=2^nextpow2(length(u)) % ближайшая к числу отсчетов степень двойки

scompl=fft(u,Nfft); % комплексный спектр сигнала

s=abs(scompl); % амплитудный спектр сигнала

phi=180/pi*angle(scompl); % фазовый спектр сигнала

figure; % создание нового окна

f =0:Nfft-1; % вектор номеров частотных отсчетов ДПФ

f=(f/(Nfft-1))*Fs; % вектор отсчетов частоты для ДПФ

stem(f,s); % отображение амплитудного спектра

title('Spectre abs(scompl(f))');

xlabel('Frequency, n*Fs, [Hz]');

ylabel('amplitude s(f), [V]');

figure;

phi=unwrap(phi); % сглаживаем график фазового спектра

plot(phi); % построение фазового спектра

title('Spectre angle(scompl(f))');

xlabel('Number, n, [pcs] ');

ylabel('angle s(f), [degree]');

П ри n=2

При n=3

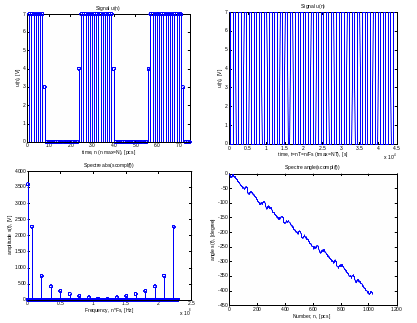
Вывод: при увеличении разрядности амплитуда увеличилась , т.е. амплитуда сигнала стала передаваться точнее. Возрастает амплитуда спектральных составляющих, т.к. увеличилась амплитуда сигнала.