1.5 Законы равновесия и принцип оптимизации процессов

Существенным вопросом, определяющим состояние системы, является степень ее удаления от состояния равновесия. Системы, находящиеся в состоянии равновесия, не меняют своего состояния во времени. Такими системами являются, например, однородные системы (газ, жидкость), у которых давление и температура одинаковы во всех частях.

Для выведения такой системы из состояния равновесия необходимо влияние на нее извне, например путем механического или теплового воздействия.

В инженерном деле одним из важнейших вопросов является вопрос о направлении изменения в состоянии системы при внешнем воздействии. Исследование этого вопроса опирается на два положения термодинамики: принцип Ле-Шателье и правило фаз Гиббса.

Согласно принципу Ле-Шателье, в системе, выведенной из состояния равновесия, происходят изменения, направление сил которых противоположно направлению сил, выводящих систему из равновесия. Применяя принцип Ле-Шателье к конкретным процессам, мы можем установить какие параметры нужно изменить, чтобы вызвать необходимые для производства изменения в состоянии системы.

Правило фаз Гиббса устанавливает зависимость между числом компонентов системы К, числом фаз f и числом степеней свободы S

Правило фаз Гиббса используется при решении вопроса о равновесии в многофазных системах.

Пусть имеется закрытый сосуд, в который налит раствор этилового спирта в воде. В этой системе число фаз – 2: пар и жидкость. Число компонентов тоже 2: этиловый спирт и вода. Следовательно, число степеней свободы равно 2.

Параметрами, определяющими состояние этой системы, будут температура, давление и концентрация спирта. Значит, из этих трех параметров мы можем произвольно устанавливать 2, например концентрацию и температуру. Давление же, определяемое природой системы, устанавливается независимо от нас.

Правило фаз позволяет установить количество параметров, определяющих равновесие системы, которые могут быть выбраны произвольно.

При проведении любого процесса всегда возникает возможность выбора нескольких вариантов решения. Один из них будет наиболее целесообразным. Выбор наиболее целесообразного варианта получил название оптимизации. В качестве критерия оптимизации чаще всего выбирается минимум времени и затрат на производство продукции. Следует отметить, что этот критерий связан со стоимостью энергии, рабочей силы и материалов, что создает некоторую неустойчивость критерий. Оптимизация всегда сводится к нахождению наиболее выгодного компромисса между значениями параметров, противоположно влияющих на процесс.

1.6 Моделирование процессов и аппаратов

1.6.1 Сущность теории подобия и моделирования процессов.

Изучение процессов с целью получения уравнений, необходимых для их анализа и расчета, можно проводить чисто теоретически. Этот наиболее желательный путь исследования сводится к составлению и решению математических зависимостей, чаще всего дифференциальных уравнений, полностью описывающих процесс.

Дифференциальные уравнения описывают целый класс однородных по своей сущности явлений, и для выделения из него конкретного явления необходимо ограничить указанные уравнения дополнительными условиями (условиями однозначности).

Условия однозначности включают: геометрическую форму и размеры системы, то есть аппаратуры, в которой протекает процесс; существенные для данного процесса физические константы, участвующих в нем веществ; начальные условия, к числу которых относятся начальная скорость, начальная температура, начальная концентрация и т.п.; граничные условия, характеризующие состояние на границах системы, например равенство нулю скорости жидкости у стенок трубы и т.д.

Таким образом, дифференциальные уравнения должны решаться в соответствии с условиями однозначности в устанавливаемых последними пределах.

Однако многие процессы характеризуются большим числом переменных и настолько сложны, что зачастую даже нельзя составить систему дифференциальных уравнений, исчерпывающе описывающих данный процесс.

Таким образом, теоретический вывод расчетных зависимостей, необходимых для проектирования аппаратуры, часто оказывается невозможным. В таких случаях для нахождения связи между величинами, характеризующими процесс, прибегают к экспериментальному исследованию, то есть к проведению опытов.

На основе опытных данных часто получают эмпирические уравнения , которые являются частными и не могут быть распространены на условия, отличные от тех, для которых они получены. Эти частные эмпирические уравнения имеют известную ценность и используются в инженерной практике.

Однако наиболее плодотворно такое осуществление экспериментов, которое позволяет обобщать результаты опытов и распространять их на широкий круг явлений, подобных изученному, но отличающихся численными значениями характерных параметров, например, размеров аппарата, основных физических свойств среды и т.д. Это достигается при использовании для обработки опытных данных методов теории подобия.

Теория подобия является учением о методах научного обобщения эксперимента. Применение теории подобия часто позволяет вместо дорогостоящих трудоемких опытов на промышленной аппаратуре выполнять исследования на моделях значительно меньшего размера; помимо этого, опыты можно проводить не с рабочими (часто вредными и опасными) веществами и не в жестких условиях реального производственного процесса, а с другими (модельными) веществами в условиях, отличающихся от промышленных.

Методы теории подобия лежат в основе масштабирования и моделирования процессов. Основные положения обобщаются теоремами подобия, которые лежат в основе практического применения теории подобия.

1.6.2 Теоремы подобия.

Первая теорема подобия была сформулирована Ньютоном. Согласно этой теореме при подобии систем всегда могут быть найдены такие безразмерные комплексы величин, которые для сходственных точек данных систем одинаковы, то есть подобные явления характеризуются численно равными критериями подобия.

Покажем это на примере движения тел, описываемого общим законом механики

Выделим в двух подобных системах (натуре и модели) две частицы, движущиеся подобно. Пусть в натуре на частицу массой m₁ действует сила Р₁, сообщая ей ускорение . В модели сходственная частица массой m₂ под действием силы Р₂ приобретает ускорение . По второму закону Ньютона

и

При подобном движении частиц, для сходственных точек натуры и модели константы подобия выражаются отношениями , и . Следствием подобия этих переменных является подобие сил:

.

Отношение сил обусловливающих движение частиц, должно быть равно отношению возникающих при этом инерционных сил. Значит

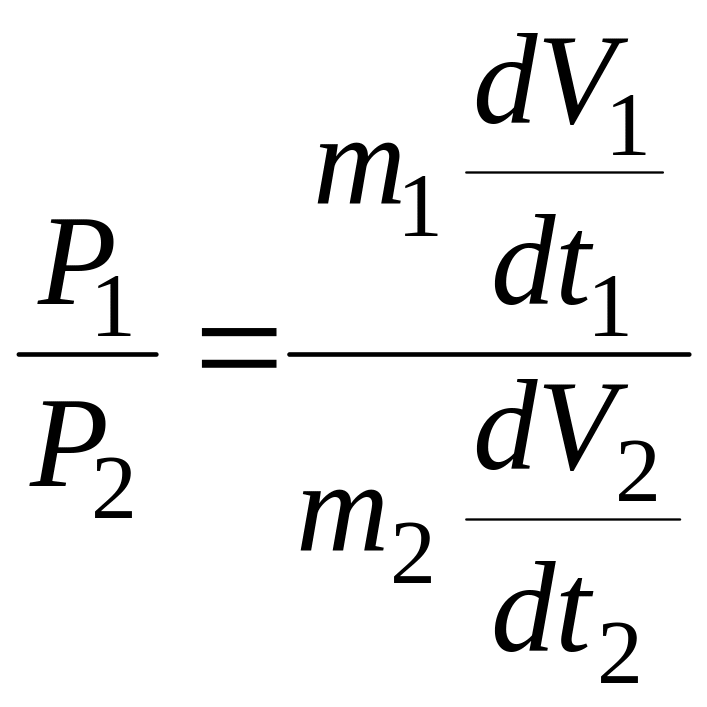, или

Отношения приращений величин, входящих в константы подобия, можно заменить отношениями самих величин, то есть знаки дифференциалов могут быть отброшены.

Таким образом

или

Откуда

Величину С, состоящую из констант подобия, называют индикатором подобия. На основании этого выражения первая теорема подобия может быть сформулирована так: у подобных явлений индикаторы подобия равны единице.

Заменяя константы подобия отношениями соответствующих величин и перенося в левую часть все величины для натуры, а в правую для модели находим

.

Таким образом, получен безразмерный комплекс величин, значения которого одинаковы для сходственных точек обеих систем. Этот комплекс называют критерием Ньютона и обозначают

или учитывая, что .

Таким образом, в случае механического подобия двух систем произведение силы на длину, деленное на массу и квадрат скорости для любой пары сходственных точек натуры и модели, имеет одно и то же численное значение.

Такая формулировка также соответствует первой теореме подобия. Из нее следует, какие конкретные физические величины нужно измерять при экспериментальном исследовании данного процесса.

Вторая теорема подобия была доказана Букингемом и Федерманом. Согласно этой теореме решение любого дифференциального уравнения, связывающего между собой переменные, влияющие на процесс, может быть представлено в виде зависимости между безразмерными комплексами этих величин, то есть между критериями подобия.

Если обозначить критерии подобия через П₁, П₂, …, П_п, то решение дифференциального уравнения может быть представлено в общем виде:

Такие уравнения называют уравнениями в обобщенных переменных (обобщенными), или критериальными уравнениями.

Критерии подобия составленные только из величин, входящих в условия однозначности, называют определяющими. Критерии же, включающие также величины, которые не являются необходимыми для однозначной характеристики данного процесса, а сами зависят от этих условий, называют определяемыми.

Из критериального уравнения, рассчитав предварительно значения определяющих критериев, находят значение определяемого критерия, а из него – значение интересующей нас величины. Таким образом, если определяемым является некоторый критерий П₁, то критериальное уравнение удобнее представлять в виде

Вторая теорема подобия отвечает на вопрос, как обрабатывать результаты опытов, проведенных на моделях; их надо представлять в виде функциональной зависимости между критериями подобия.

Третья теорема подобия, или теорема Кирпичева и Гухмана, формулирует необходимые и достаточные условия подобия явлений: подобны те явления, которые описываются одной и той же системой дифференциальных уравнений и у которых соблюдается подобие условий однозначности.

Подобию условий однозначности при идентичности дифференциальных уравнений, описывающих процессы, отвечает равенство определяющих критериев подобия. Значит, третья теорема подобия может быть сформулирована и так: явления подобны, если их определяющие критерии численно равны.

Следствием равенства определяющих критериев, является равенство определяемых критериев для модели и натуры. Поэтому зависимость, полученная обобщением результатов опытов на модельной установке, будет справедлива для всех подобных процессов, в том числе для натуры.

Таким образом, исследование процессов методом теории подобия должно состоять из следующих этапов:

1) Получив полное математическое описание процесса, то есть составив дифференциальное уравнение и установив условия однозначности, проводят подобное преобразование этого уравнения и находят критерии подобия.

2) Опытным путем на моделях устанавливают конкретный вид зависимости между критериями подобия, причем полученное обобщенное расчетное уравнение справедливо для всех подобных явлений в исследованных пределах изменения определяющих критериев подобия.

В тех случаях, когда из-за сложности явления или процесса не удается составить его полное математическое описание в виде систем дифференциальных уравнений, а возможно лишь в самом общем виде представить зависимость между физическими величинами и геометрическими параметрами, характеризующими процесс, вид зависимости можно найти на основе анализа размерностей физических величин, вошедших в уравнение. Этот метод, введенный в инженерную практику Бриджменом, базируется на так называемой П-теореме, являющейся частным случаем второй теоремы подобия.

П-теорема – формулируется следующим образом: всякое уравнение, связывающее между собой п физических величин, среди которых m величин обладают независимыми размерностями, может быть преобразовано к уравнению, связывающему (п-m) безразмерных комплексов, составленных из этих величин.

П – теорема имеет большое значение при проведении экспериментального исследования, позволяя находить связь не между отдельными физическими переменными, а между некоторыми их безразмерными соотношениями, составленными по определенным законам. При этом число переменных уменьшается на число использованных основных единиц измерения, что существенно упрощает условия проведения эксперимента.